基于概率烈度的结构抗震损伤可靠性分析

林 立，杨伟军

(1.厦门理工学院，福建厦门361024;2.长沙理工大学，湖南长沙410076)

一般将抗震结构在使用期限［0，T］内的地震可靠度ps表达为:

式中:pf为结构在使用期内发生损伤的概率;pf(R＜SA)是给定地震加速度A时结构的条件损伤概率;f(A)dA是强度在A和(A+dA)之间的地震动加速度的发生概率;R为结构抗力;S为地震响应［1］。

长期以来，采用该方法进行结构抗震可靠性的计算，只是简单地将结构的地震作用结果划分为“损伤”与“非损伤”，以“R＜S”作为结构损伤与否的唯一标准。基于此所做的分析虽然在一定程度上能够体现结构的抗震性能，但是却无法直观地指示结构发生不同损伤状态的可能。而在实际应用中往往需要判断结构在地震作用下可能发生什么程度的损伤，发生的概率如何，即通过分析对应于不同结构损伤等级的失效概率，来评价结构的抗震风险。因此有必要探讨更加合理的可靠性分析方法，使其适用于结构抗震损伤状态的概率分析。

1 基于损伤状态等级与概率烈度的结构抗震可靠性计算

1.1 基于损伤状态分级标定的抗震可靠性分析

当结构的失效概率比较大的时候，结构的失效概率对功能函数的分布类型不是很敏感，这时可以直接假定功能函数服从正态分布，从而为结构可靠度的计算带来方便［2］，即:

式中:sn为第n级损伤的损伤状态指标界限值;S为损伤指标，根据混凝土多孔砖砌体墙片试验结果［2］，可用式(4)表示:

则

将式(5)视为功能函数，可用求解可靠度指标的方法来求解，其中i为结构楼层。

由于本研究的混凝土多孔砖砌体属于新型墙材，缺乏大量实际工程的震害资料来对“损伤指标”进行检验和标定。根据混凝土多孔砖砌体墙片试验分析结果，损伤指标均值为15.56［3］，小于黏土实心砖的损伤指标均值，因此参考偏于保守的黏土实心砖的标定结果［4］，根据损伤状态指标均值划定损伤等级指标范围如表1。

表1 损伤状态指标范围Table 1 Range of damage state

在地震确定烈度Ij的作用下，结构整体发生n级损伤的概率pf，n可以表示为:

式中:pf，i，n，j为设防区结构第 i层在 Ij烈度地震作用下发生第n级损伤的概率，即:

1.2 考虑概率烈度的结构损伤状态可靠性分析

以往对结构抗震可靠性进行分析时，常常忽视地震设防区地震烈度发生的概率性，并且简单地将地震烈度与地面峰值加速度取为一一对应的关系，以简化计算，但是这与结构抗震实际不符，影响分析结果的精度。因此需要进一步分析抗震设防区实际发生烈度的概率，以此为基础分析结构不同损伤状态的可靠性将更加合理［5］。

对我国华北、西北和西南45个城镇的地震烈度概率分布的统计分析表明［6］，50年设计基准期内最大地震烈度的概率分布符合极值Ⅲ型分布，近似可得代表性地震烈度在设计基准期内发生的概率为:

式中:ω为地震烈度上限值，ω=12;I为地震设防烈度，发生时概率为F(I)=90%;Im为众值烈度，Im=I-1.55;e为常系数，e=2.718;k为形状系数。

由于不少国家都是以50年内超越概率为10%的地震强度作为设计标准k［7］，统一按这个概率水平来确定形状参数，计算结果列于表2。

表2 形状系数Table 2 Shape factor

考虑确定性地震烈度在设计基准期内发生的概率In，计算得各地震设防区发生低于一定烈度地震的概率，并进一步将发生烈度按下面的原则离散化:P(Ij)=P(In)-P(In-1)(j=6，7，8;n=6，7，8);P(I5)=P(In)(n=5)。结果如表3。

表3 地震发生烈度的离散概率Table 3 Discrete probability of seismic intensity /%

引入概率烈度关系后，式(8)即为建在Id设防区的房屋结构第i层在地震作用下发生第n级损伤的概率，表达为:

则房屋整体发生n级损伤的概率表达为:

1.3 结构损伤指标及结构随机变量的统计特征及概率分布

对于确定性结构，可以认为地震输入的随机性对结构抗震可靠度的影响远大于结构随机参数的影响，根据墙片试验结果［8］，混凝土多孔砖砌体结构主要考虑结构最大位移um和累计能量耗损ε作为结构随机变量的影响。

在地震持续时间td上的层间最大位移um通常定义为:

式中:ui(t)是结构层间位移随机响应。

层间最大位移um，i服从极值 I分布［9］，其概率分布函数为:

其概率密度函数为:

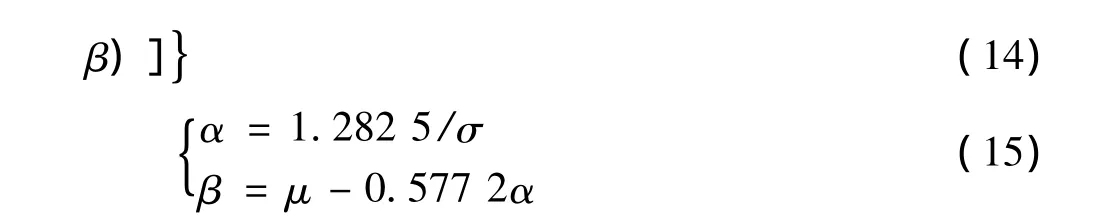
式中:参数μ和σ为极值I型分布的数学期望与均方差。

结构第i层在td时段内的累积滞变耗能ε，定义为:

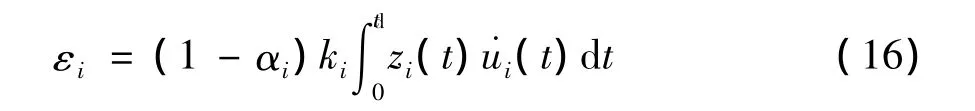
式中:ki，αi，zi(t)，td分别为结构初始刚度、第 2 刚度系数、延滞位移和地震作用持续时间。

假设最大位移um和累计能量耗损ε完全相关，则损伤指标si为两个随机变量的线性组合，服从对数正态分布，其均值和方差分别为［10］:

累积损伤指标的概率密度函数为:

2 混凝土多孔砖砌体结构的抗震可靠性分析算例

一幢8层混凝土多孔砖砌体房屋，其平面立面和侧视如图1。屋面恒载5.0 kN/m2，活载0.7 kN/m2;楼面恒载4.0 kN/m2，活载2.0 kN/m2;墙体自重4.81 kN/m2。

图1 混凝土多孔砖砌体房屋示意(单位:m)Fig.1 Concrete porous brick masonry building

采用JC算法来求解可靠度指标，计算得到不同的地震设防区，各楼层发生1～5级不同的损伤状态的概率，将计算结果列于表4。

表4 混凝土多孔砖砌体房屋损伤状态概率Table 4 Damage state probability of concrete porous brick masonry building /%

从表4可以看出:

1)底层一般是全结构的薄弱层，与按传统的动力可靠性计算方法分析结论相符［10］。

2)同一房屋随着楼层越低，则结构损伤程度越严重，与动力可靠性分析的结论——楼层越低失效概率越高也较一致［10］。

3)随着地震区发生大烈度地震的概率增大，混凝土多孔砖砌体房屋发生较为严重的损伤的概率也越大，与动力可靠性分析结果一致［10］。

不同设防区房屋底层的损伤状态概率的分析曲线如图2。可以看出在6度区，底部主要保持基本完好和轻微损伤，7度区以轻微和中等损伤为主，8度区以中等损伤为主，倒塌和严重损伤的概率均控制在一个较小的范围。另外可以看出同一结构在不同地震烈度设防区，其损伤状态概率有非常明显的变化，地震烈度对结构的破坏状态有很大影响。

图2 结构底层损伤状态概率曲线Fig.2 Curve of bottom layer damage state probability

3 结语

采用混凝土多孔砖砌体结构的损伤指标来标定结构的损伤状态等级，使得传统的可靠度计算方法可应用于多级的结构抗震损伤状态分析。同时还考虑抗震设防区地震烈度发生的概率性，建立基于概率烈度及损伤状态的结构抗震可靠性计算公式，提高了计算分析的精度。该方法改进了传统的结构抗震可靠性分析结果的单一性，将结构抗震损伤状态分级量化，明确了结构的分级抗震目标，为进一步的结构抗震损伤分析和风险判断提供直接的分析基础。通过一幢混凝土多孔砖砌体结构案例的计算，其分析结果与前期研究中动力可靠性的分析结果相一致，验证了本方法具有一定的适用性和有效性。

本方法的分析精度取决于损伤状态的标定方式，对于能够应用准确的损伤指标对结构损伤状态进行精确标定的结构而言都具有较好的分析效果。对于本文的混凝土多孔砖砌体而言，由于缺乏长期、实际的震害资料，更加精确可靠的结构损伤状态风险量化分析，还将依赖于长期的应用过程中进一步收集震害数据，优化结构损伤状态标定来完成。

［1］ 李桂青，李秋胜.工程结构时变可靠度理论及其应用［M］.北京:科学出版社，2001.

［2］ Bruce R E.Implementing structural reliability in professional practice［J］.Engineering Structures，2000，22:106-115.

［3］ 杨伟军，林立，杨春侠.混凝土多孔砖砌体房屋抗震可靠度分析［J］.工程力学，2007，10(24):100-104.

Yang Weijun，Lin Li，Yang Chunxia.The research on seismic reliability of concrete perforated brick masonry structure［J］.Engineering Mechanics，2007，10(24):100-104.

［4］ 江近仁，洪峰.多层砖房的地震可靠度分析［J］.地震工程与工程振动，1985，5(4):13-27.

Jiang Jinren，Hong Feng.The analysis of the seismic reliability on multi-storey brick building［J］.Earthquake Engineering and Engineering Vibration，1985，5(4):13-27.

［5］ 林立，卓卫东，范立础.基于概率烈度的地面加速度峰值分布分析［C］//第四届全国防震减灾工程学术研讨会会议论文集.北京:中国建筑工业出版社，2009.

［6］ 胡聿贤.地震工程学［M］.北京:地震出版社，1988.

［7］ Dymiotis C，Kappos A J，Chryssanthopoulos M K.Seismic reliability of masonry-infilled RC frames［J］.Journal of Structural Engineering，ASCE 2001，127(3):296-305.

［8］ 杨伟军，张振浩，林立.基于破坏指标界限值的结构抗震可靠度分析［J］.地震工程与工程振动，2010，30(1):77-83.

Yang Weijun，Zhang Zhenhao，Lin Li.Research on seismic reliability of structure based on boundary value of damage index［J］.Earthquake Engineering and Engineering Vibration，2010，30(1):77-83.

［9］ 欧进萍，王光远.结构随机振动［M］.北京:高等教育出版社，1998.

［10］杨春侠，施楚贤，杨伟军.混凝土多孔砖砌体模型房屋抗震性能试验研究［J］.建筑结构学报，2006，27(3):84-92.

Yang Chunxia，Shi Chuxian，Yang Weijun.Experimental investigation on pseudo-dynamic test of concrete perforated brick masonry building model［J］.Journal of Building Structures，2006，27(3):84-92.