指挥决策实体层次结构设计方法

周翔翔， 姚佩阳， 尹忠海

(空军工程大学，a.电讯工程学院，西安 710077;b.理学院，西安 710051)

0 引言

以网络为中心的协同作战是现代战争的基本作战形态和达成战争目的的主要手段［1］。在这种作战模式下，战役作战任务通常分解为一系列相关的子作战任务，这些子作战任务是由多个指挥决策实体(Tactical Command Decision-Making Entity，DM)根据其控制的作战平台资源共同筹划实施的［2］。指挥决策实体之间进行信息共享可以改善决策质量、进行平台资源共享以分担作战任务，有利于提高指挥决策的效能。然而仅仅依靠完全对等的协作会降低决策效率，这就需要根据作战任务，在指挥决策实体之间建立一定的层次结构［3－5］，使得角色和分工不同的DM在任务的协作处理上获得较高的效率。

面向战役作战任务，生成一个扁平合理的DM层次结构主要有以下两个优点［6－8］:1)降低DM间的协调代价，提高DM间的决策速度和效率;2)当DM组织遭受打击时，根据DM之间的层次关系，便于设计有效的指挥决策职责接替规则，保证组织功能的有效运作。

文献［7，9－11］对DM间的层次结构设计方法进行了研究，给出了由协作交流网生成指挥控制树的Gomory-Hu树构造算法，该方法属于一种破圈法。

本文描述了指挥决策实体层次结构设计的基本概念，建立了数学模型，并从并链成树的角度，给出了指挥决策实体(DM)间层次结构的形成方法。

1 基本概念描述

设计指挥决策实体(DM)间的层次结构涉及以下几种基本概念。

作战任务(Combat Task，T)是作战单元为完成所赋予的作战使命而实施的一次行动，是战场中作战资源的某一种或几种功能协同执行的行为集合。

指挥决策实体(Command Decision-Making Entity，DM)是一个具有信息处理并进行决策的实体，它根据其控制的作战平台资源，筹划并实施作战任务［12］。

作战平台资源(Combat Platform Resource，R)是处理作战任务所需的物理资源实体，是决策者执行任务的凭借［2，4］。平台包括火力实体和感知实体。

决策实体通过对平台的管理控制来执行使命任务，决策实体间通过平台在任务上的协作便构成了协作交流网。协作交流网反映了决策实体之间的任务协作关系，并不是决策实体之间的实际组织关系。

指挥控制树体现了DM间的层次结构。指挥控制树确定了DM之间的决策关系，以DM为节点，DM间的指挥关系的链接为边，由根节点与其他节点建立起有向链接关系，树中没有环路。

本文以协作交流网G(V，E，U)为基础，设计DM之间的层次结构，即指挥控制树，其形式化描述为

其中，F为下文将详细描述的DM层次结构设计算法。

2 层次结构设计方法

2.1 模型建立

对于协作交流网G(V，E，U)，其生成树并不唯一，需要根据具体问题求解具备某种条件的G(V，E，U)的生成树。如在通信网络中的最小生成树、Stenier树等。针对DM层次结构特点，构造的指挥控制树需要描述任务协作与指挥控制特性的生成树越扁平越好，这样可以减少DM之间交互协作的复杂度。下文首先给出一些定义，之后建立DM层次结构模型。

每个DM与其他DM之间的协作包括信息交换和任务协作，本文借鉴文献［9－11］的工作负载定义，仅从任务协作的角度给出DM协作量的定义，该协作量值即为协作交流网中边的权值。

定义1任意两个DM(vi，vj)之间的任务协作量uij为vi和vj协作完成任务的工作量之和，则

定义2路径长度。设协作交流网(连通图)G(V，E，U)中任意两个节点vi和vj的最短路径为Pmin(Vi，Vj)，则 vi到 vj的路径长度为路径 Pmin(Vi，Vj)的边权值和，即

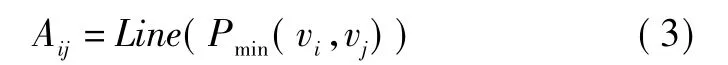
其中，Line为获取路径边权值和的算子。两个节点vi和vj的路径长度表示vi和vj之间的协作功能链的任务协作总量。

定义3树高。设 T=T(V，E′，U′)为树，vb为 T的根节点，令h为由根节点vb至树T的各节点路径长度的最大值，即

则h为树T的树高。

定义4扁平生成树。设协作交流网G(V，E，U)的生成树记为T，T的树高记为H(T)，G的生成树集合记为Q，树高最小的生成树T0称为扁平生成树，即T0满足

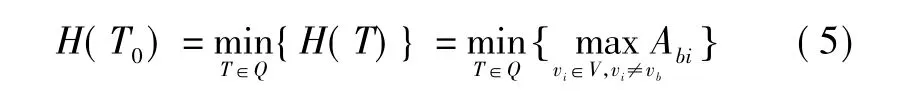
传统意义上将树中节点的最大层次定义为树高，本文定义的树高是树中节点的最大路径长度。从根节点DM到其他每个DM都存在一个指挥功能链，树高表示了指挥功能链上任务协作总量的最大值，而扁平树是最大路径长度最小(指挥功能链的任务协作量总和最大)的生成树。本文需要构造的指挥控制树即为协作交流网的扁平生成树，即

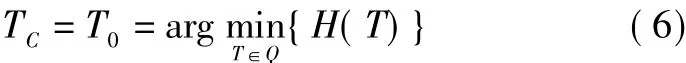
2.2 算法分析

根据上文构造的模型，以下逐步给出扁平指挥控制树的构造方法。

定理1设协作交流网G(V，E，U)为连通图，vs，ve，记 vs，ve间的最短路为 Pmin(vs，ve)，则 Pmin(vs，ve)为链。

证明 由于 vs≠ve，设 vs，ve间的最短路 Pmin(vs，ve) 为 vse1v1e2v2…eivi…ejvj…emve，如图 1a 所示。

若 Pmin(vs，ve)不是链，则必有路径 Pmin(vs，ve)的中间节点 vi，vj，使得 vi=vj，即 Pmin(vs，ve)如图 1b 所示。

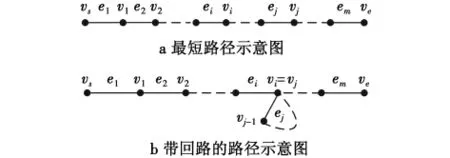
图1 路径示意图Fig.1 Sketch map of path

即在路径Pmin(vs，ve)中存在一条由 vi至 vj的回路，显然，路径P′min(vs，ve)=vse1v1e2v2…eiviej+1vj+1…emve是一条由vs至ve的最短路径，与vs至ve的最短路矛盾，故最短路一定是链。

定理2设协作交流网G(V，E，U)为连通图，vb为取定的根节点，vb至图G中任意节点vi的最短路径记为Pmin(vb，vi)，若最短路是唯一的，则所有最短路的并

为图G的一棵生成树。

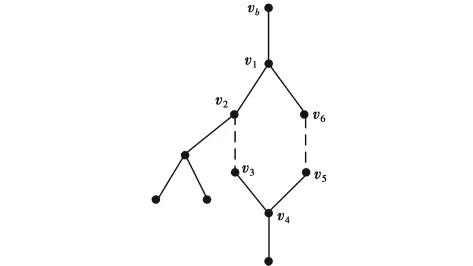
图2 带回路的非树示意图Fig.2 Sketch map of non-tree with loop

图2 中 v1→v2→v3→v4→v5→v6→v1构成了回路，显然vb→v1→v2→v3→v4是vb至v4的最短路，同时vb→v1→v6→v5→v4也构成vb至v4的最短路，与最短路唯一的假设矛盾，故T构成树。

定理3按式(7)构造的生成树T0是最扁平生成树。

证明 设存在另一棵生成树T0′使得H(T0)，则必存在某一节点v0，使得T0′中由根节点vb至v0的距离小于树T0中由vb至v0的距离，则T′0中由vb至v0的路径是一条比T0中由vb至v0距离更短的路径，这与T0中由vb至v0是最短路的结论矛盾，故T0是扁平生成树。

对于给定的协作交流网G(V，E，U)，取定V中节点vb为根节点，vb至G中任一节点vi的最短路记为Pmin(vb，vi)，则vb到所有其他节点的最短路的并即为G(V，E，U)的一个生成树，且该树为扁平生成树。即指挥控制树 TC为 G(V，E，U)的所有最短路 Pmin(vb，vi)的并，则

例如对于具有6个节点的协作交流网，取定v3为根节点，v3到其他节点的最短路径分别为:v3→v1、v3→v4→v6→v2、v3→v4、v3→v4→v6→v5、v3→v4→v6，则以 v3为根节点的指挥控制树如图3所示。

图3 最短路径并操作示例Fig.3 Example of the shortest path and operation

上述分析为解决指挥控制树构造问题提供了切实可行的方法，但其实现还需要两个前提:1)保证任意两个节点之间的最短路唯一;2)需要确定指挥控制树的根节点。下面分别给出这两个问题的解决方法。

1)节点之间唯一最短路的选择方法。

协作交流网G(V，E，U)中任意两个节点vi和vj之间的最短路径并不一定唯一。为保证求出的最短路径满足定理2所要求的唯一性条件，本文对Floyd算法进行了限定，限定算法中每次处理的节点都是满足条件序号最小的节点，即每次处理都首先选择距离最近的节点，当多个节点的距离相同时选择序号最小的节点。

2)指挥控制树根节点的确定方法。

定义5最大路径长度、平均路径长度。

设协作交流网(连通图)G(V，E，U)中任意vi到其他所有节点的最大路径长度为

vi到其他所有节点的平均路径长度为

本文确定指挥控制树根节点的方法是依次按照3个规则实施，直到满足条件的节点唯一。这3个规则的目的都是查找满足一定条件的节点(或节点集)，规则分别为协作交流网中节点到其他所有节点的最大路径长度最小、节点到其他所有节点的平均路径长度最小、节点序号最小。

2.3 算法步骤

基于以上讨论，本文给出以下指挥控制树的构造算法步骤。

1)根据协作交流网中DM之间关于作战任务的任务协作量信息，计算协作交流网中任意两个指挥决策实体vi和vj的边权值，构成网G的边E的权值集合U={uij|1≤i，j≤nV，uij=u(ek)，ek∈E}，uij=0 表示两个节点之间没有链接，uii=0表示节点到自己没有自回路。

2)根据指挥决策节点之间唯一最短路的选择方法，获得协作交流网中任意vi、vj的唯一最短路径，为Pmin(vi，vj)。

3) 根据任意 vi、vj的 Pmin(vi，vj)，采用式(9)、式(10)，求得vi的和

4)基于3个层次规则的指挥控制树根节点的确定方法，求得指挥控制树的根节点为vb。

5) 将根节点 vb到其他所有节点 vi，i=1，2，…，nV，的唯一最短路径进行合并，得到指挥控制树TC。

3 算法应用及对比分析

以一次登岛战役作战为例，其作战使命任务为登陆抢占敌方的机场和港口，为后续部队向纵深推进扫清障碍。根据这个使命任务和作战环境可以将作战任务分解为［2，10］10 个作战任务。

本文设定10个作战任务的作战平台配置已完成，并对作战平台资源进行了分组，每组作战平台资源设置一个DM。作战平台可分为6个组，故设置了6个DM。DM之间由于共同执行任务而建立任务协作关系，形成DM之间的协作交流网如图4所示。

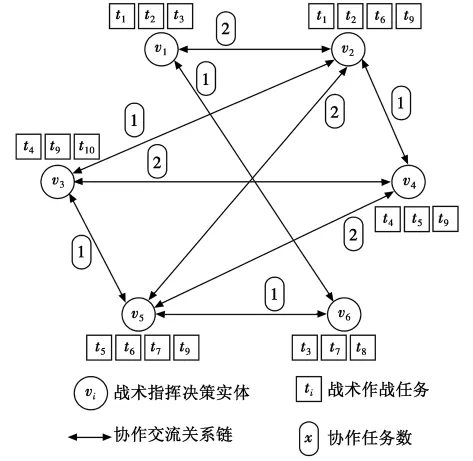
图4 协作交流网算例Fig.4 Collaboration-intercourse net

图4 中两个DM之间的值表示两者协作的任务数量。表1中给出了DM之间的协作的各个任务的协作量。其中表示DM vi与DM vj之间的关于协作任务k的协作量。

表1 DM之间的任务协作量Table 1 Task collaboration value between DMs

根据表1，计算协作交流网的边权值为

基于图4所示的协作交流网，结合协作交流网的边权值，根据节点之间唯一最短路的选择方法，采用式(3)、式(9)、式(10)可以计算得到DM之间的路径长度关系如表2所示。

表2 DM节点间的路径长度Table 2 Path length between DMs

根据表2的结果，由于到其他节点的最大路径长度最小的节点只有v5，故选择v5为指挥控制树的根节点。以v5为根节点，采用本文算法得到的指挥控制树如图5所示。

图5 生成的指挥控制树Fig.5 The created command and control tree

在现实中，担负一个战役任务的决策实体间的组织关系可以是层次式、网络式或混合式的，本文设计的指挥控制树作为一种层次结构，明确了决策实体间的决策与交流结构，为之后的多实体间的作战计划制定奠定了基础。若某个任务由单个决策实体担负，则该决策实体具有该任务的独立决策权;若某个任务由多个决策实体担负，则根据决策实体在指挥控制树中的位置，明确在该任务的计划制定中的信息流向、指令流向和决策权。比如任务t9由4个决策实体v2、v3、v4、v5共同担负，信息由 v2、v3、v4流向 v5，指令由 v5流向 v2、v3、v4，v5负责作战任务t9计划制定中的协调和各决策实体作战方案的融合。

4 结论

本文以设计适应现代战争需求的指挥决策实体的层次结构为目标，建立了协作交流网的扁平生成树模型;从并链成树的视角，给出了扁平生成树构造算法;在算法实现的技术处理上，给出了确定网中任意两个节点之间唯一最短路径的方法，以及基于3个层次规则的指挥控制树根节点的确定方法。实验结果表明本文方法是有效的。

［1］ 阳曙光，时剑，李为民.联合火力打击协同式指挥控制模式及其军事概念建模［J］.电光与控制，2008，15(2):1-4.

［2］ 阳东升，刘忠，张维明.组织模型与自适应机理分析［J］.系统工程与电子技术，2008，30(10):1929-1933.

［3］ LEVCHUK Y N，LUO J，LEVCHUK G M，et al.A multifunctional software environment for modelling complex mission and devising adaptive organizations［R］.Arlington:Office of Naval Research，2005.

［4］ LEVCHUK G M，LEVCHUK Y N，WEIL S A，et al.Persuade:Modeling framework for the design of modular army organizations［C］//Proceedings of the 2006 Command and Control Research and Technology Symposium，San Diego，CA，2006:1-24.

［5］ 周道安，张东戈，常树春.C2组织指挥控制关系的形式化描述［J］.指挥控制与仿真，2008，30(4):13-17.

［6］ 阳东升，张维明，刘忠，等.指控组织设计方法［M］.北京:国防工业出版社，2010.

［7］ LEVCHUK G M，LEVCHUK Y N，LUO J，et al.Normative design of organizations-part II:Organizational structure［J］.IEEE Transactions on Systems，Man and Cybernetics，2002，32(3):360-375.

［8］ WANG L，KANG Q，WU Q D.Nature-inspired computation effective realization of artificial intelligence［J］.Systems Engineering Theory ＆ Practice，2007，27(5):126-134.

［9］ 修保新，张维明，刘忠，等.基于粒度计算和遗传算法的C2组织结构设计方法［J］.自然科学进展，2007，17(5):662-671.

［10］ YU F.Advanced optimization techniques with applications to organizational design and graph-based inference［D］.University of Connecticut，2007.

［11］ 刘宏芳，阳东升，刘忠，等.兵力编成结构裁剪中指挥关系优化研究［J］.国防科技大学学报，2006，28(4):99-104.

［12］ YU F，TU F，PATTIPATI K R.Integration of a holonic organizational control architecture and multiobjective evolutionary algorithm for flexible distributed scheduling［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A:Systems and Humans，2008，38(5):1001-1017.