如何处理立体几何中空间图形的翻折问题

☉江苏省姜堰中学 宋元海

立体几何是每年高考的必考内容之一，在高考中占有重要的地位.只要对近几年高考试题稍作分析我们就不难看出高考对立体几何考查的重点与难点相对比较稳定.立体几何综合问题中的将平面图形折叠成空间几何体的问题也是高考试题中经常出现的一种题型.笔者结合对几道例题的解析来简要阐述此类问题的解决方法.

对于翻折问题一定要理清翻折前后的不变关系和不变量.通常在折痕的同侧的位置关系和线的长度、角度的大小不变，但是在折痕两侧的线的长度、角度以及位置关系都有变化，这一点是处理翻折问题的关键之处.

【典型例题】在直角梯形ABCD中，AB∥CD，AB=2BC=4，CD=3，E为AB中点，过E作EF⊥CD，垂足为F（如图1），将此梯形沿EF折起，使得平面ADFE垂直于平面FCBE（如图2）.（2011年苏北四市模拟）

（1）求证：BF∥面ACD；

（2）求多面体ADFCBE的体积.

【解析】（1）证明：因直角梯形ABCD中，AB∥CD，AB=2BC=4，CD=3，E为AB中点，EF⊥CD，垂足为F，则BCFE为正方形.

设BF和CE的交点为O，则O是正方形BCFE的中心.

因平面ADFE垂直于平面FEBC，则AE和DF都垂直于平面FEBC.

取AC的中点H，则由三角形的中位线性质，可得OH平行且等于AE的一半，OH平行且等于DF，则四边形OHDF为矩形.

则OF平行于DH.

由DH⊆平面ACD，OF不在平面ACD内，得OF∥面ACD，BF∥面ACD.

（2）把多面体ADFCBE分成两个棱锥：三棱锥A-BCE和四棱锥C-AEFD.

由题意可得CF⊥平面AEFD，AE⊥平面BCFE.

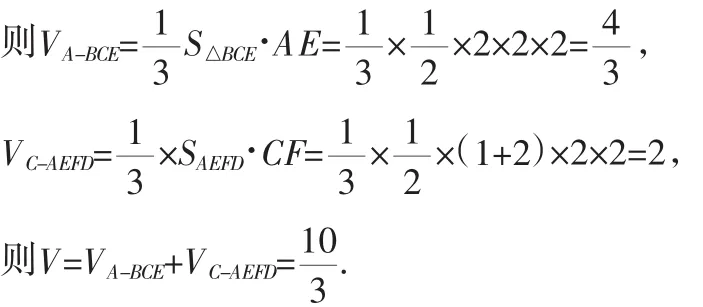
点评：本题主要是通过平面图形翻折问题处理空间线-线关系和线-面关系即直线和平面平行的判定定理的应用，从识图、想图、画图的过程的角度考查了空间想象能力.而对空间图形的处理能力是空间想象力深化的标志，是高考从深层次上考查空间想象能力的主要方向.

【原题拓展】（2010年盐城市）已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+，过A作AE⊥CD，垂足为E，G、F分别为AD、CE的中点，现将△ADE沿AE折叠，使得DE⊥EC.

（1）求证：BC⊥平面CDE；

（2）求证：FG∥平面BCD；

（3）在线段AE上找一点R，使得面BDR⊥面DCB，并说明理由.

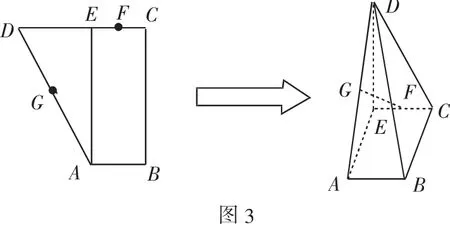
【解析】（1）如图所示：由已知得：DE⊥AE，DE⊥EC，

则DE⊥面ABCE，DE⊥BC.

又BC⊥CE，则BC⊥面CDE.

（2）取AB中点H，连接GH，FH.

则GH∥BD，FH∥BC，则GH∥面BCD，FH∥面BCD.

则面FHG∥面BCD，则GF∥面BCD.

（3）分析可知，R点满足3AR=RE时，面BDR⊥面BDC.

理由如下：取BD中点Q，连接DR、BR、CR、CQ、RQ.

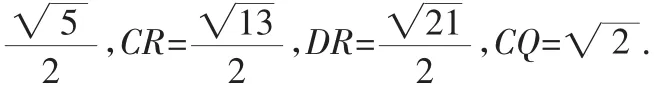
又在△CBD中，CD=CB，Q为BD中点，则CQ⊥BD，则CQ⊥平面BDR，则面BDR⊥面BDC.

点评：本题考查的知识点是平面与平面垂直的判定，直线与平面平行的判定，直线与平面垂直的判定，熟练掌握空间直线与平面之间平行及垂直的判定定理、性质定理、定义、几何特征是解答此类问题的关键.在解决本题过程中要注意平面图形在翻折的前后同侧和两侧点、角度、线等之间关系是否发生改变；解题过程中要充分挖掘和利用这些不变关系和不变量；同样这也是解决平面图形翻折问题的关键之处.

总而言之，解决有关空间图形的翻折问题时，要注意对翻折前后线线、线面位置关系、所成角度及距离加以比较，要灵活运用其中的不变关系和不变量（主要是平行、垂直关系和角度的大小、线段的长度等）.对于不变量的计算和证明可结合原图型来计算和求证；对于变化了的量应在翻折后的立体图形中来求解.对某些翻折后不易看清的关系和量，可结合原图形去分析、计算，即将空间问题转化为平面问题进行处理.由此可见，将平面图形翻折成空间图形，既是实际应用问题的需要，又具有考查学生空间想象能力、逻辑推理、数学实践、综合分析问题能力的功能，这就要求我们高中数学教师在平时的课堂教学中注重这些能力的培养，以便实现课堂教学效果的最大化.