通性通法,一招制胜的法宝:由“ 怎样做到分类不重不漏”引发的思考
2012-08-27江苏省江浦高级中学文昌校区於有海
☉江苏省江浦高级中学文昌校区 於有海
一、规律探索
1.问题给出
《中学生数学》(2010年1月上)(高中)中“怎样做到分类不重不漏”[1]一文,运用多重分类的方法处理2007年高考广东卷一题.
例1 已知a是实数,函数f(x)=2ax2+2x-3-a,如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围.
有兴趣的读者可参阅原文.
笔者认为多级分类讨论对学生来说要做到分类不重不漏并非易事,我们不妨翻阅各地高考试卷,凡涉及多重分类讨论的大都是一些压轴题,而此题不一定有此难度.当然,解决此题的方法一定也很多,下面笔者谈谈个人对此题乃至一类问题的一点浅见.
2.问题分析
函数y=f(x)在区间[-1,1]上有零点
⇒方程2ax2+2x-3-a=0在区间[-1,1]上有实数解

3.问题简解
解:函数y=f(x)在区间[-1,1]上有零点,等价于方程2ax2+2x-3-a=0在区间[-1,1]上有实数解,即方程(2x2-1)a=3-2x(*)在区间[-1,1]上有实数解.
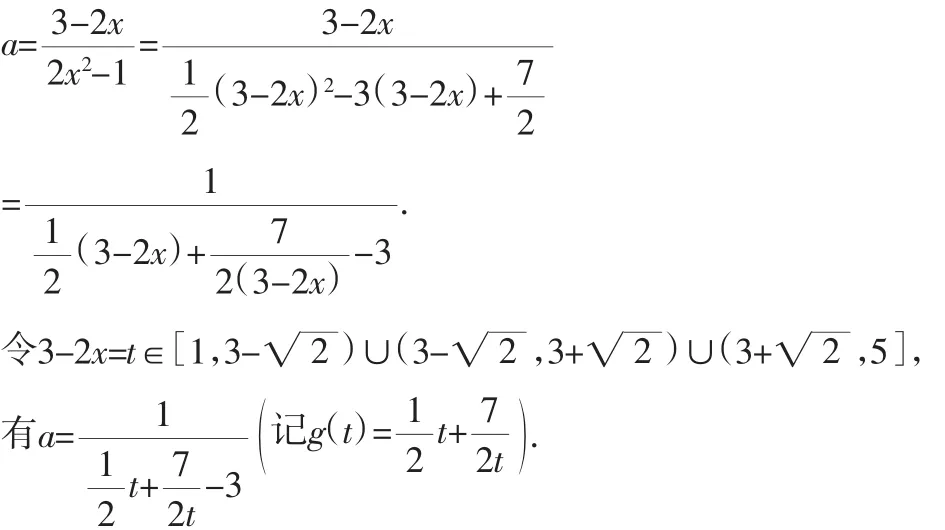
如图1.


二、殊途同归
1.方法提炼
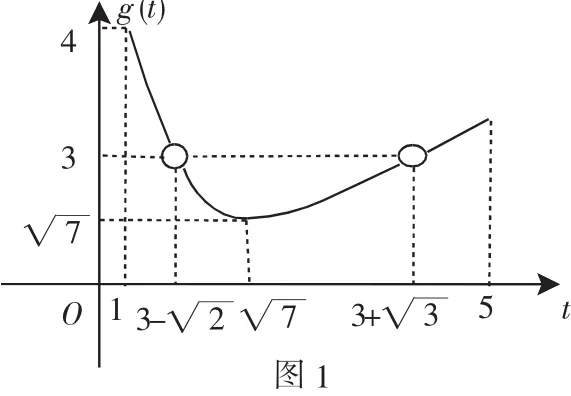
例1实质是“方程有解”问题.命题结构:∃x∈[a,b] ,使得方程(fx)=m成立.
如图2所示,如果命题成立(方程有解),那么m应该在两条直线(包括直线)之间的区域内变化,而此区域正是函数y=f(x)的值域,由此可归纳出这类问题的处理流程:
方程有解⇐求函数值域⇐找函数⇐变量分离
(变量分离这步需要根据具体题目考虑使用与否,下面不再说明)

2.姊妹命题
“方程有解”问题我们不妨先到此,下面来看看“方程无解”、“不等式恒成立”、“不等式能成立”与“方程有解”问题的区别和联系.
(1)“方程无解”问题
命题结构:∀x∈[a,b],都有方程f(x)=m不成立.
如图3所示,如果命题成立(方程无解),那么m应该在两条直线(不包括直线)之外的区域内变化,而此区域正是函数y=f(x)的值域的补集,由此可归纳出这类问题的处理流程:
方程无解⇐求函数值域的补集⇐找函数⇐变量分离

(2)“不等式恒成立”问题
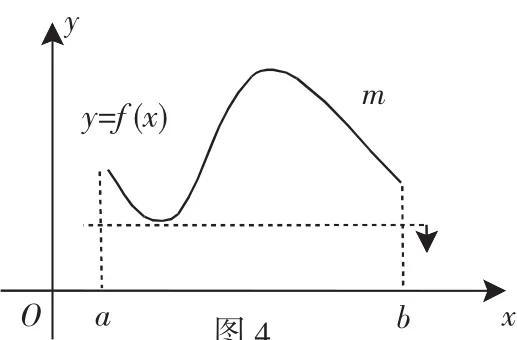
命题结构:∀x∈[a,b],都有不等式f(x)>m成立.
如图4所示,如果命题成立(不等式恒成立),那么m应该在直线(不包括直线)以下的区域内变化,所以只要解出函数y=f(x)的最小值,使这个最小值大于m即可,由此可归纳出这类问题的处理流程:
不等式恒成立⇐求函数最值⇐找函数⇐变量分离
(3)“不等式能成立”问题
命题结构:∃x∈[a,b],使得不等式f(x)≤m成立(即不等式有解).
如图5所示,如果命题成立(不等式能成立),那么m应该在直线(包括直线)以上的区域内变化,所以只要解出函数y=f(x)的最小值,使这个最小值小于或等于m即可,由此可归纳出这类问题的处理流程:
不等式能成立⇐求函数最值⇐找函数⇐变量分离

3.形异质同
到这里,读者应该能够看出方程有解(无解),不等式恒成立(能成立),这两类看上去毫不相关的问题,其实质上却是相同的——都是求函数的值域或最值.因此我们可给出统一的处理流程:
方程有(无)解,不等式恒(能)成立⇐求函数值域或最值⇐找函数⇐变量分离
三、规律运用
例2 (2010年天津卷第16题)




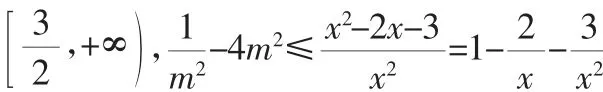


本题从表面上看,题目中的式子结构很复杂,但本质上就是不等式恒成立问题,因此由规律知只要求出函数最值就可以解出答案.这样,了解这类问题的本质不仅为我们节省了审题的时间,更为我们考试信心的提升带来了不可估量的作用.
四、教学反思
1.重视通性通法的教学
不管是方程有解(无解)问题,还是不等式恒成立(能成立)问题,都可以归结到函数的值域与最值问题范畴——通性,解决这类问题实质就是求函数的值域或最值——通法.
通性通法的熟练掌握,有利于学生利用这种通法而“一招制胜”.例2的选择主要目的在于让学生通过比较,近一步感受通性通法的优点,从而达到多题一解、一招制胜的效果.当然,例题也还有其他的解法(本文在此不作说明),笔者认为,通性通法是解决这类问题的正餐,利用性质等巧法则是配菜.
2.重视几何图形的辅助解析
华罗庚说过“数无形时少直觉,形少数时难入微”,从几何直观上分析问题与用代数方法解几何问题同样重要,而在面对抽象、难于理解或从数的角度去解决问题出现繁杂,导致解题效率低下甚至失败时,不妨换个方式——用几何图形——来进行尝试,这样可能会挖出题中一些隐含的几何条件,从而帮助理解,甚至解决问题.这正如美国数学家斯蒂恩所说:如果一个特定的问题可以被转化为一个图形,那么就整体地把握了问题,并且能创造性地思索问题的解法.
3.重视常见函数的值域与最值的教学
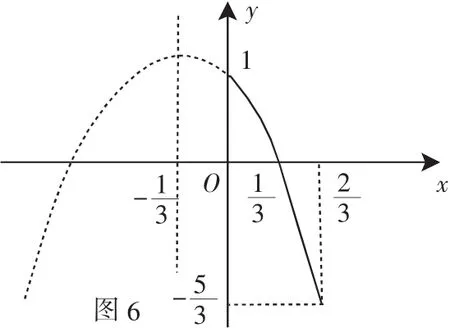
(1)常见函数
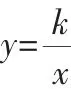
(2)求函数值域与最值的方法
函数的值域与最值的求法,一直以来都是探究的热点,其中不乏优美的解法,但是这些解法往往伴有一些特殊的要求,正是这些“要求”导致学生“一听就懂,一做就错”.笔者认为过分的发散而不及时总结则为无用功.
其实前一节所列出的常见函数,在求它们的值域与最值时都有固定的方法,如一次函数、反比例函数、指数函数可用单调性;二次函数可判断对称轴与定义域之间的关系;正弦函数、余弦函数可画图像.当遇到有几个常见函数组合而成的函数时可考虑使用不等式或导数,即:把握一种方法,巧用两个工具.
总之,对于《课标》中要求不明确之处,应本着“简单”、“易知”的原则去把握.这就要求教师在教学过程中,应做到有的放矢,把该讲的内容讲透,不易过分拔高或降低要求,学生能够掌握常见函数的值域或最值的基本解法即可.
1.陈大康.怎样做到分类不重不漏[J].中学生数学,2010(1上).
2.王忠.2009年江苏卷解析几何题解题分析与教学反思[J].中学数学(高中版),2009(10).
3.江苏省教育科学研究院课程教材研究中心,江苏省中小学教学研究室.江苏省普通高中课程标准教学要求[M].南京:江苏教育出版社,2007.
