点到直线距离公式的解题功效

☉湖南省长沙市稻田中学 莫 俐

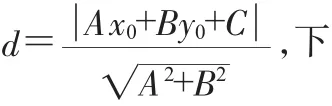
一、寻找最近

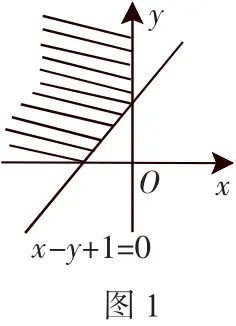
解析：画出可行域，如图1所示.依题意知在阴影区域内找一点，使其到原点的距离最小.最小距离即为原点到直线x-y+1=0的距离，进而可确定所求点的坐标.

二、求参数的值

主要是指已知点到直线的距离，求点坐标中的参数或直线方程中的参数，解题的关键是合理运用距离公式.

例2 直线y=kx+3与圆（x-3）2+（y-2）2=4相交于A，B两点，若，则实数k的值是______.

解析：如图2，由已知得圆心的坐标为O（3，2），半径为2，即OB=2.过点O作OD⊥AB于点D.由点到直线的距离公式，可得OD=，在Rt△BOD中，利用勾股定理即可求得k的值.

三、求三角形的高

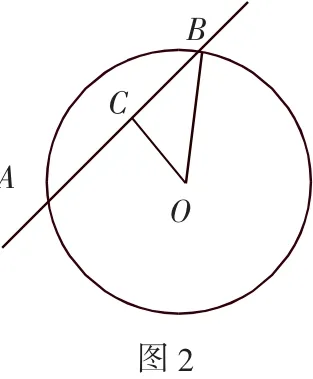
例3 已知点A（0，2），B（2，0）.若点C在函数y=x2的图像上，则使得△ABC的面积为2的点C的个数为（ ）.

A.4 B.3 C.2 D.1

答案：

四、判断直线与圆的位置关系

答案：相切

五、求轨迹方程

例5 求两条直线l1：3x+4y+1＝0，l2：5x+12y-1＝0的交角平分线方程.

解析：由角平分线上的点到两边的距离相等的性质，同样可转化为点到直线距离来解决.

设P（x，y）是交角平分线上任一点，则P到l1，l2的距离相等，即

整理，得所求的方程为7x-4y+9＝0或8x+14y-1=0.

六、求直线方程

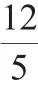
解析：过两直线的交点的直线，可用直线系方程来设.

设这条直线方程为（7x+7y-24）+λ（x-y）=0，即

（7+λ）x+（7-λ）y-24=0.

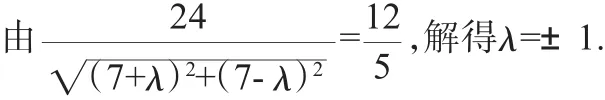
所求的直线方程是4x+3y-12=0或3x+4y-12=0.