感悟合情推理的两种方法

☉江苏省盱眙中学 刘兰华

合情推理是根据已有的事实，经过观察、分析、比较、联想，再进行归纳、类比，然后提出猜想的推理.常用的合情推理有归纳推理和类比推理，下面通过具体例子剖析合情推理.

一、归纳推理

归纳推理就是依据一类事物的部分对象具有某种性质特征，推出这类事物的所有对象都具有这种性质的推理，它是从特殊到一般的过程.它是合情推理的一种形式.

例1 已知集合A={3m+2n|m＞n且m，n∈N}，若将集合A中的数按从小到大排成数列{an}，则有a1=31+2×0=3，a2=32+2×0=9，a3=32+2×1=11，a4=33=27，…，依此类推，将数列依次排成如图1所示的三角形数阵，则第6行第3个数为（ ）.

A.247 B.735 C.733 D.731

分析：根据题意可知，每一行所排的数成等差数列，只要求出前5行已经排了多少个数，就可以求出第6行第3个数是数列中的第几项，即可求得结果.

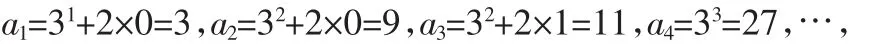
故a18=36+2×2=733.故选C.

点评：考查根据已知条件分析数据并归纳的能力，其中求出第6行第3个数是数列中的第18项，是解题的关键，属中档题.

例2（2012年江苏高三模拟）图2是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行；依此类推，则第63行从左至右的第5个数应是_______.

分析：注意数字排列的规律，每行的行号数和这一行的数字的个数相同，奇数行的数字从左向右依次减小，偶数行的数字从左向右依次增大，每行中相邻的数字为连续正整数.

点评：本题以网络运作的蛇形模型为素材，考查学生合情推理的能力，考查学生分析、解决问题的能力，解题的关键是发现数字排列的规律.

二、类比推理

根据两类不同事物之间具有某些类似（或一致）性，推测其中一类事物具有与另一类事物类似（或相同）的性质，这样的推理叫做类比推理.类比推理是由特殊到特殊的一种推理形式.它是合情推理的另一种形式.

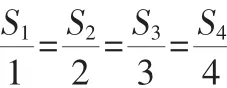
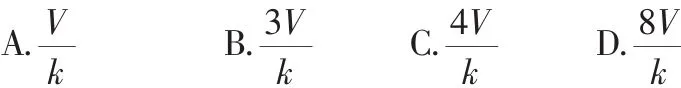
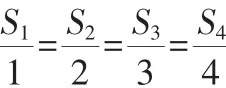
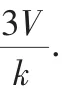
所以选择C.

点评：本题主要考查三棱锥的体积计算和运用类比思想进行推理的能力.解题的关键是理解类比推理的意义，掌握类比推理的方法.根据平面几何的许多结论，可以通过类比的方法，得到立体几何中相应的结论.当然，类比得到的结论是否正确，则是需要通过证明才能加以肯定的.

例4（2012年浙江第二次五校联考）平面内与直线平行的非零向量称为直线的方向向量，与直线的方向向量垂直的非零向量称为直线的法向量.在平面直角坐标系中，利用求动点轨迹方程的方法，可以求出过点A（2，1）且法向量为n=（-1，2）的直线（点法式）方程为－（x－2）+2（y－1）=0，化简后得x－2y=0.则在空间直角坐标系中，平面内经过点A（2，1，3），且法向量为n=（-1，2，1）的平面（点法式）方程化简后的结果为______.

点评：类比推理是由特殊到特殊，类比常用于立体几何与平面几何、向量运算与实数运算、圆锥曲线、等差数列与等比数列中，类比是从人们已经掌握了的事物的性质，推测正在研究中的事物的性质，它以现有认识为基础，类比出新的结果，类比的结果是带有猜测性的，因此不一定正确，但它具有发现的功能.

在数学教学中，通过训练学生的合情推理能力，可以使学生将数学知识的学习过程变成模拟数学家当时探索的过程，进而学会自觉地探索数学规律，发现数学结论，从而真正成为学习的主体.