向量客串 匠心独具

☉湖南省长沙市明德中学 何 玲

向量是数学中的重要概念之一，由于它具有几何和代数的“双重身份”，因此成为中学数学知识的一个交汇点，成为联系各种知识的媒介，特别是在处理度量、角度、平行、垂直等问题时，向量工具有其独到之处，尤其是解决解析几何问题中，它像“一个客人”，以其匠心独具的思路去剖析一个个棘手的题目，能够大显身手.请看下面例题.

例1 如图1，给定点A（a，0）（a＞0）和直线l：x=-1，B是直线l上的动点，∠BOA的角平分线交AB于点C，求点C的轨迹方程，并讨论方程表示的曲线类型与a值的关系

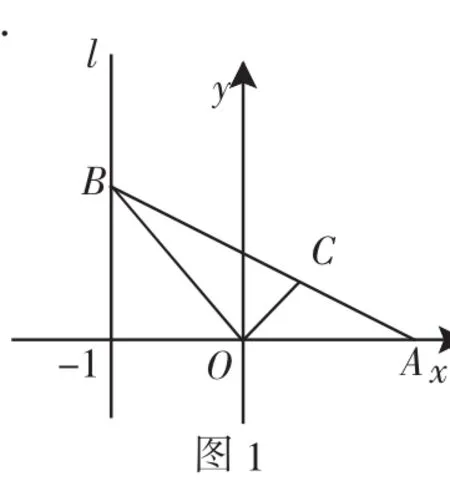
常规解法：根据题意，设B（-1，b）（b∈R），则直线OA与直线OB的方程分别为y=0和y=-bx，设点C（x，y），则有0≤x＜a.由OC平分∠BOA，知点C到OA，OB的距离相等，根据点到直线的距离公式，有：

把b代入①，得：

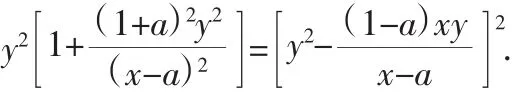
整理可得：y2［（1-a）2x2-2ax+（1+a）y2］=0.②

当y=0时，b=0，∠BOA=π，点C的坐标为（0，0），满足②式，

则点C的方程为：（1-a）x2-2ax+（1+a）y2=0（0≤x＜a）.

（1）当a=1时，y2=x（0≤x＜1）表示一段抛物线.

当0＜a＜1时，表示一般椭圆；当a＞1时，表示双曲线的一部分.

当b=0时，∠BOA=π，点C（0，0）也适合方程.

综上，点C的轨迹方程为：（1-a）x2-2ax+（1+a）y2=0（0≤x＜a）.

当0＜a＜1时，表示椭圆的一部分，当a＞1时表示双曲线的一部分.

常规解法：略.

常规解法：略.

常规解法：略.

巧妙解法：设C（x，y），则（x，y）=（3α，α）+（-β，3β）=（3α-β，α+3β）.

小结：解决这类问题的关键是把解析几何题目中的条件向量化，这无形中加大了题目的难度，提高了对学生综合能力的要求，学生解答这类题目的关键是把向量的条件表达的几何意义挖掘出来，或者直接运用向量的坐标运算解题.