三角形面积之比的结论的简证与拓展

●叶国芳 (嵊州市第一中学 浙江嵊州 312400)

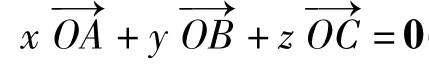
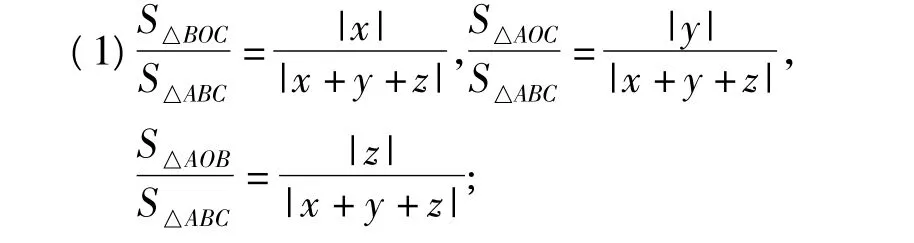
(2)当 x，y，z全不为 0，即点 O 不在△ABC 各边所在的直线上时，

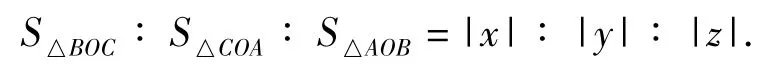
对结论(1)的证明，文献［2］与文献［1］的方法略显生硬，本文给出较自然、简便的证法，并将结论拓展.

1 对结论(1)的简证

对x+y+z≠0的证明，文献［2］中已给出 x，y，z中有一个为0的情形，也很容易证明.本文对x，y，z全不为0的情形，给出简证.

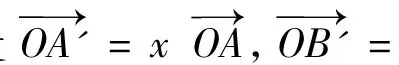
故O是△A'B'C'的重心，于是

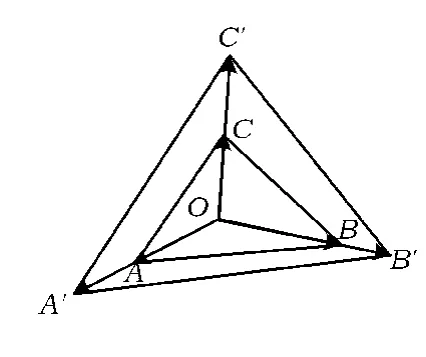
图1

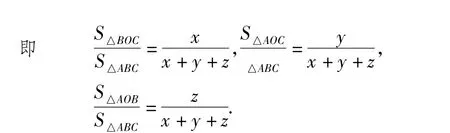
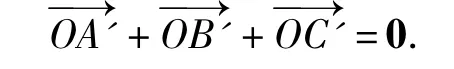
故O是△A'B'C'的重心，于是

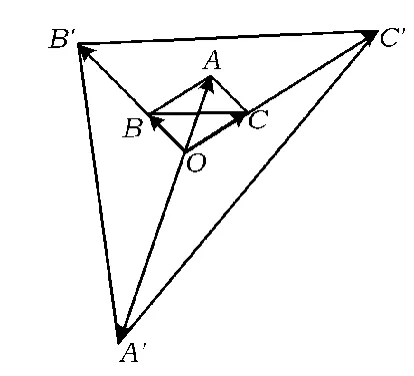
图2

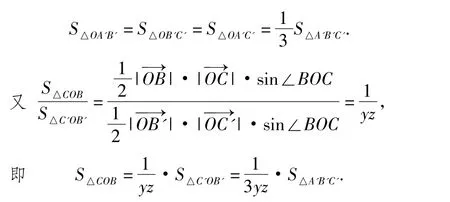
设点B到AA'的距离为h，点B'到AA'的距离为h'，则

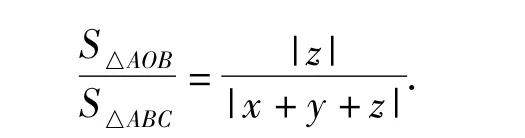
(3)若 x，y，z中有 2 个为负，不妨设 x＜0，y＜0，z＞0，将 y移项后，便得 -y＞0，即 x＜0，-y＞0，z＞0，同情形(2)，同理可得结论成立.

2 结论的拓展

a3，a4不全为 0)，则(2)当点O不在四面体ABCD各面上时，从而a4=0，与题设矛盾.

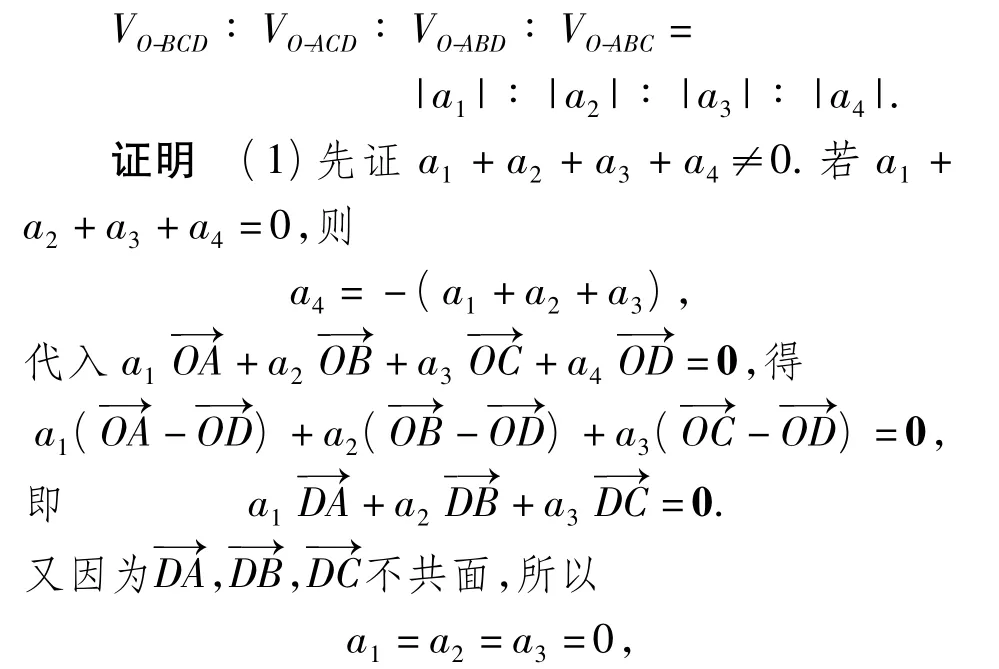
a1，a2，a3，a4中有 1 个或 2 个为 0 的情形，也很容易证明，这里不再赘述.下面证明 a1，a2，a3，a4全不为0时的情形：

①若 a1，a2，a3，a4＞ 0，则点O在四面体ABCD内，如图3.

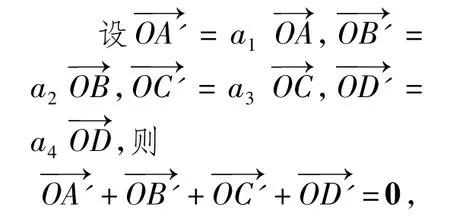
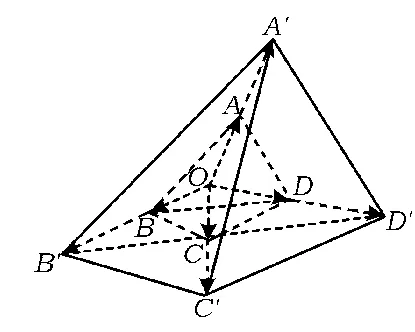
图3

故O是四面体A'B'C'D'的重心，因此

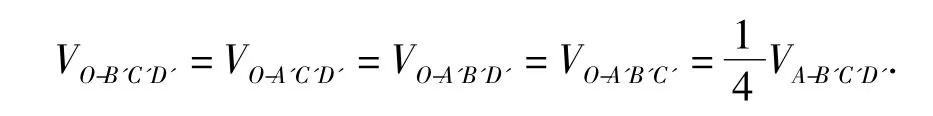
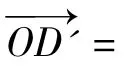
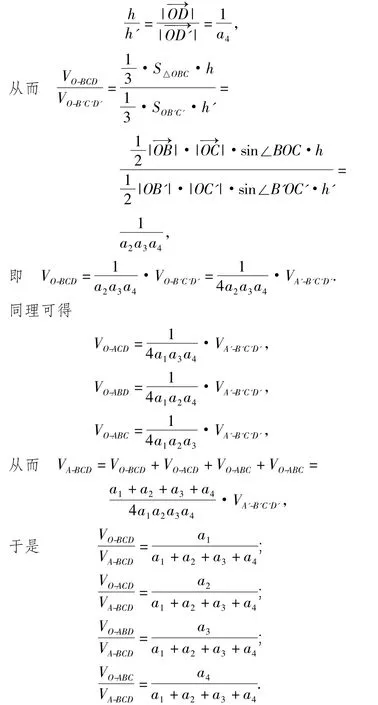
②若 a1，a2，a3，a4中有1 个或2 个或3 个为负数，仿此亦可证得(此处略).

(2)当 a1，a2，a3，a4全不为 0 时，显然有

［1］ 康小峰.一道调研试题的探究［J］.数学通讯，2010(3)：27-28.

［2］ 宋广志，邢友宝.三角形面积之比的结论修正与简证［J］.数学通讯，2010(16)：39.