探究一类特殊的伸缩变换

●杨亢尔 (武岭中学 浙江奉化 315500)

普通高中课程标准实验教科书《数学(选修)》4-4第1讲“坐标系”给出平面直角坐标系中坐标伸缩变换的定义如下：

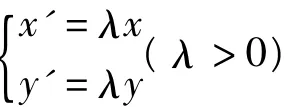
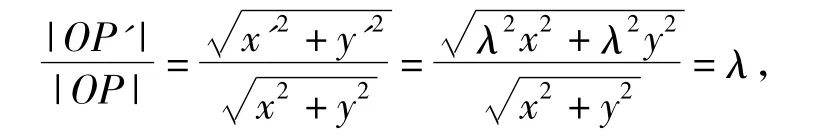
此时称曲线C与C'相似，相似比为λ，称点O为相似中心(如图1所示).

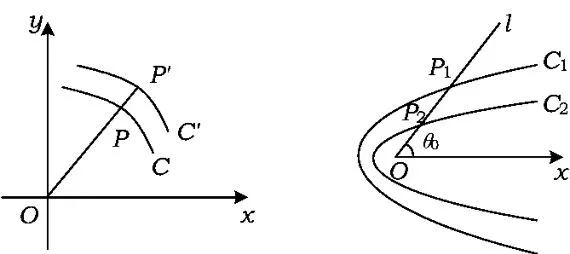
图1 图2

圆锥曲线在相似变换下有以下性质：

性质1 任一圆锥曲线经过相似变换后离心率不变.

证明由于抛物线的离心率都为1，性质1对抛物线显然成立.

同理可得双曲线在相似变换后的离心率不变.

如果把圆看作离心率为0的圆锥曲线，那么其离心率也保持不变.

综上所述，任一圆锥曲线经过相似变换后的离心率不变.

性质2 离心率相等的圆锥曲线都相似.

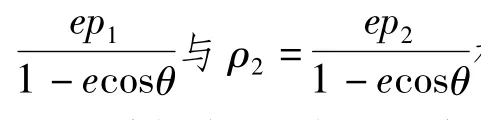
过极点O引任一直线 l：θ=θ0交曲线 C1，C2于点 P1，P2，则

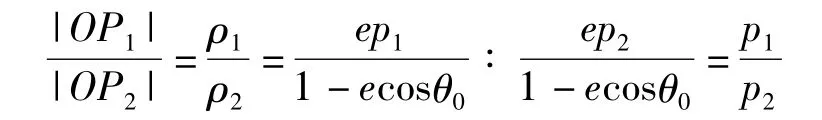
性质3 若2条圆锥曲线相似，则它们相应的焦点、中心、顶点都可作为相似中心.

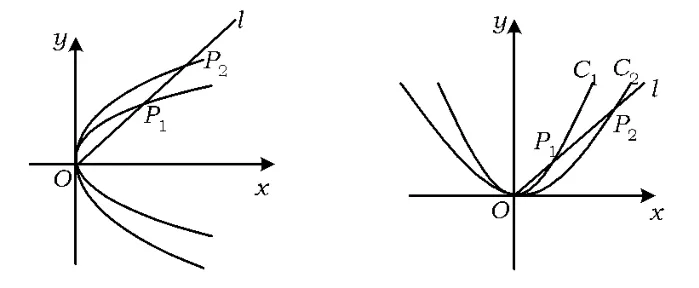
图3 图4

证明由性质2知，离心率相等的圆锥曲线的焦点可作为相似中心.

下面先证椭圆的顶点可作为相似中心.如图3所示，让离心率相等的2个椭圆的一个相应顶点重合，过该点的轴所在直线也重合，设这2个椭圆的中心为 Oi(ai，0)(i=1，2)，则它们的曲线方程为

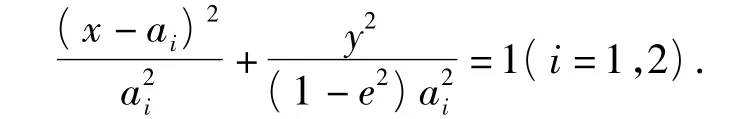
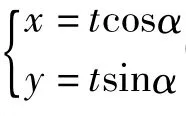
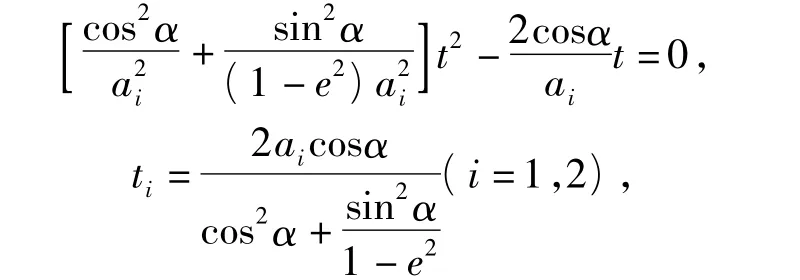
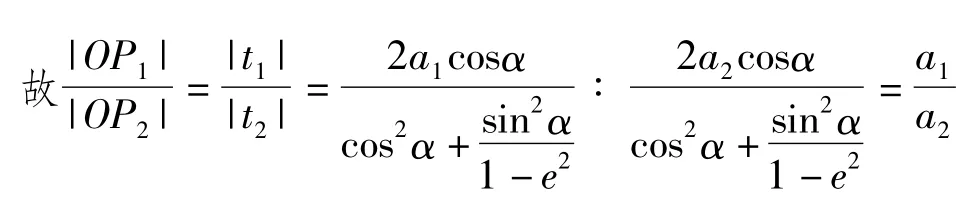
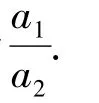
对于抛物线x2=2p1y与x2=2p2y，如图4所示，从它们的顶点出发任作一直线l，分别交2条抛物线于点 P1，P2.设直线 l的方程为 y=kx，易得P1(2p1k，2p1k2)，P2(2p2k，2p2k2)，于是

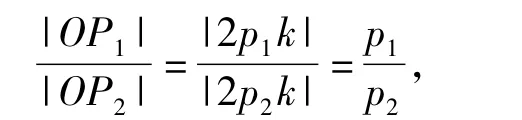
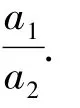
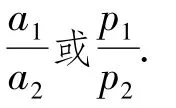
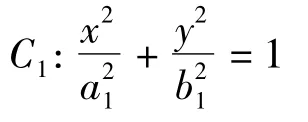
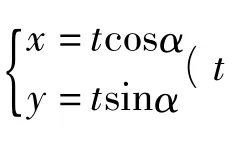
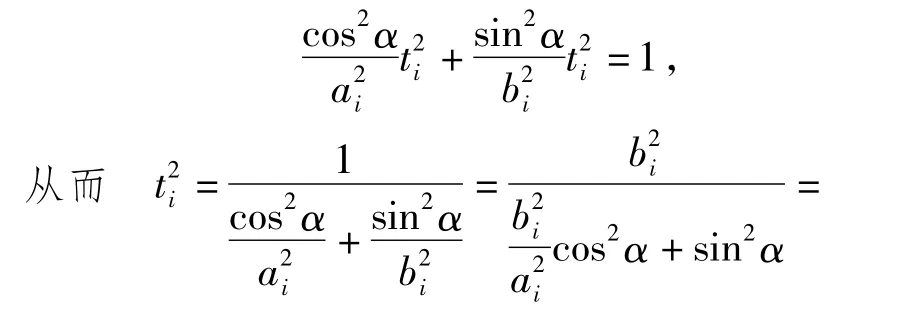
事实上，该题中2个椭圆的中心为它们的一个相似中心.

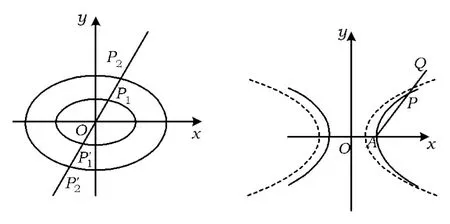
图5 图6

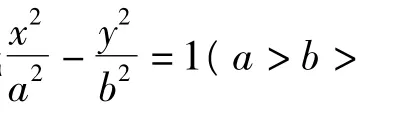
例3 如图7所示，已知抛物线y2=2p1x与y2=2p2x，过原点引3条直线与2条抛物线分别相交于点 A1，A2，B1，B2，C1，C2，求 证：△A1B1C1∽△A2B2C2.

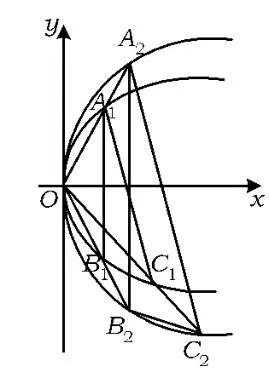
图7

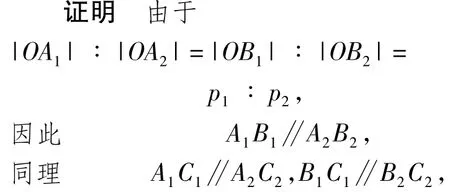
由平面几何知识知△A1B1C1∽△A2B2C2.