小题大做有必要，训练思维见功效

☉河南省鹿邑伯阳双语学校 段传礼

随着课程改革的不断推进，“题海战术”愈来愈站不住脚.如何利用有限的题目锻炼学生的思维能力呢？那就需要精选习题，精做精练，小题大做，以一当十.可以深化学生对知识的理解，进一步形成基本技能，优化思维品质，提升数学思维能力.下面就一道高考题展示其思维过程.

思维1：导数法

反思 这种解法是借助函数研究函数的单调性，再利用单调性求函数的最值，虽不是最简单的解法，但比较通用.

思维2：二次函数法

反思 注意到y＞0，想到两边平方，根号虽去不掉，但根号内可变为二次函数，把无理函数的最值问题转化为二次函数的最值问题，实现了由难到易的转化.

思维3：三角代换法

思维4：基本不等式法

由基本不等式a2+b2≤（a+b）2（ab≥0，当且仅当ab=0时，“=”成立）与（a+b）2≤2（a2+b2）（a、b∈R，当且仅当a=b时，“=”成立），即ab≥0时，a2+b2≤（a+b）2≤2 （a2+b2） 成立，可得1-x+x+3≤

思维5：均值不等式法

将函数两边平方得y2=4

思维6：柯西不等式法

y2≤（12+12）［（值的求法见思维5.故

思维7：向量法

反思分析式子特征，联想到a·b≤|a|·|b|，关键是构造向量a、b，从而求出最大值.

思维8：二元代换法

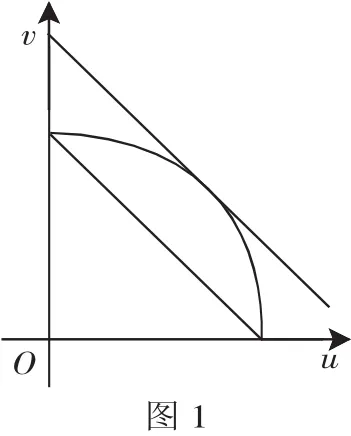
u2+v2=4（0≤u≤2，0≤v≤2）在uOv坐标系内表示的是一段圆弧（如图1）.

y=u+v表示的是直线v=-u+y在v轴上的截距.

结合图形，易求得ymax=

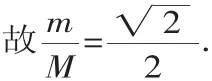
反思 把函数右端做一个恰当的变量代换，化一元函数为二元函数，这样函数便有了固定的几何意义，借助几何图形，利用解析几何的方法求出最值，比较巧妙直观.

总结

同学们在以后碰到这类题时可选择恰当的方法去解决.

通过对以上具有很强的示范性和代表性的小题进行充分的联想及适当的拓展，可以充分发挥习题的系统性和整体性的潜能，从而沟通各知识点的纵横联系，达到练一题、带一类、连一片的目的，进而使学生的认知结构得到完善，正可谓是“小题大做有必要，训练思维见功效”.