模糊推理技术在螺纹磨削工艺决策中的应用

徐 侃，李郝林

XU Kan, LI Hao-lin

（上海理工大学 机械工程学院，上海 200093）

0 引言

螺纹磨削是精密螺纹加工的主要方法，用于加工高精度和高硬度螺纹表面，常见的工件有精密丝杠、滚珠丝杠、蜗杆、螺纹量规、丝锥和螺纹铣刀等。可见，螺纹磨削的加工水平将在很大程度上影响我国数控机床等高精密工程设备的生产与制造[1]。同时，螺纹磨削的加工工艺又是影响螺纹精度的关键因素。然而，由于磨削是一个相当复杂的过程，而螺纹的磨削相对于其他简单平面磨削来说又要考虑更多因素，所以螺纹磨削加工工艺的确定便显得尤为困难。

目前，国内的螺纹磨削加工企业主要是依靠工艺技术人员根据自己多年来的实际加工经验来确定加工工艺参数。这样的工作模式虽然能够切实保证工艺参数选择的准确性，但存在诸多难以解决的实际问题。主要在于，由于螺纹磨削在国内机械加工领域并不常见，熟悉此加工方法的工艺人员显然为数不多，一旦出现人员的空缺与调整，将直接影响产品的加工与生产，且短时间内无法立即恢复。此外，加工工艺经验的传承也存在着不确定因素。为解决此问题，本文提出运用模糊推理方法，对技术人员确定的工艺参数加以处理，建立工艺参数的模糊推理规则库，并以此进行推理计算，提供合理的加工工艺参数供机床操作人员参考。

1 螺纹磨削工艺推理系统结构

本文所建立的推理系统主要由案例数据库、规则库和模糊推理程序三部分组成。系统的规则库由案例数据库中的实际加工案例建立完成。当用户将所需要查询的精确加工要求参数输入系统后，系统首先将其模糊化，即转换成语言变量的形式，再由推理机在规则库中选择合适的语言规则并得出结论，最终在解模糊化后得出精确的工艺参数值，供用户参考。该系统的结构示意图如图1所示。

图1 系统结构框图

2 用作推理的工艺参数的选定

对螺纹的磨削加工一般要进行粗磨、半精磨和精磨这三步工序，而每一步的加工又分别要考虑砂轮转速、工件转速和背吃刀量这几个工艺参数值的选择。此外，对于粗磨和半精磨这两步还有中径余量这个参数值需要确定。决定这些参数选择的主要因素包括螺纹种类、工件材料、螺距、工件直径和螺纹长度等[2]。其中，螺纹种类和工件材料这两个因素不适合以模糊化的方式输入系统，故将螺距、工件直径和螺纹长度定义为模糊推理系统的三个输入值，分别用X1, X2, X3表示。由于粗磨、半精磨、精磨这三步工序的工艺参数类型及其推理方法基本相同，本文以粗磨为例介绍整个推理过程，其工艺参数值砂轮转速、工件转速、背吃刀量和中径余量被定义为系统的四个输出值，分别用Y1, Y2, Y3, Y4表示。

3 模糊推理过程

3.1 工艺参数模糊化

未经过处理的输入输出值是有确定数值的清晰量，而模糊推理过程是通过模糊语言变量进行的，在清晰量和模糊量之间有一定的对应关系。为了实现模糊推理，必须进行清晰量的模糊化。语言变量是以自然或人工的词句作为值的变量。对应于每一语言变量，都必须定义它的各个语言值，即它的各个模糊集的隶属度函数[3]。三角形隶属函数是较为简便的一种语言值确定方式，在工业中应用广泛。故本文采用了等间距的三角形隶属度函数，即通过模糊化方法，将各输入输出参数取值区间分割为若干间距相等的模糊子集，使每个模糊子集构成等腰三角形。其中，各参数的取值区间如表1所示。

表1 输入输出参数及其取值区间

系统各参数均采用如图2所示的隶属度函数分布形式。其中，{A1, A2,…, AN}分别表示一个参数的各个模糊子集，[u, v]为该参数的取值区间。

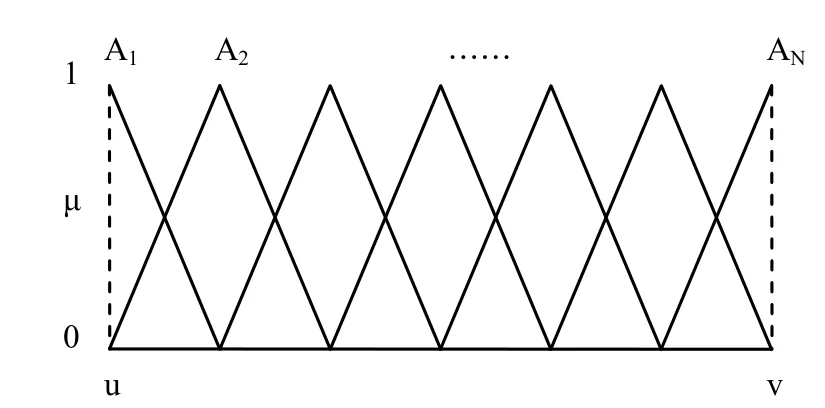
图2 隶属度函数示意图

3.2 从案例学习规则

本文的案例数据库存储了大量的技术人员的实际加工参数数据组，需要将这些数据转化生成相应的模糊规则。例如，在案例数据库的一个数据 组 {X1=p1, X2=p2, X3=p3，Y1=q1, Y2=q2, Y3=q3,Y4=q4}，确定其每一个参数的对应语言值后，一条模糊规则就被记录下来。规则可以用模糊语句表示为如下的形式：

然而，由数据组产生的规则可能会出现矛盾的情况。为了解决这个问题，需要计算由数据产生规则的匹配程度，并只接受那些矛盾的规则中匹配程度最大的规则。在一条规则中，每个输出参数都有各自的匹配度值，计算方法是将该条规则所对应的所有输入语言值的隶属度相乘，再乘以各自输出语言值的隶属度。通过这样的方法，便可依次对案例数据库中每一个数据组生成一条模糊规则，并记录在系统的规则库中。每生成一条规则，就同时计算该条规则的匹配度，并完成如下过程：1）若规则库中没有与该规则前件相同的规则，则直接存入规则库，并把该规则相应的匹配度值也存储下来。2）若规则库中存在与该规则前件相同的规则，则由该规则的匹配度与已存的匹配度相比较的大小，来决定保留或放弃该规则。

由于在从案例数据库学习规则时，案例数据组有可能不会在所有取值范围内出现，规则库列表中的某些规则就会出现空缺。参考文献[6]中对此问题有详尽的论述，并根据相似性的概念，给出了一个完成规则库补全的一般算法。

3.3 由规则推理结果

通过规则库的建立，系统便可在得到一组需要查询的磨削加工要求参数后立即推理出合适的加工工艺参数。

一组查询数据被输入后，系统首先计算这组数据在各自语言变量值上的隶属度，一般情况下，每一个数据会得到在两个语言值上的非零隶属度。假设，所需查询的螺距(mm)、工件直径(mm)和螺纹长度(mm)分别为a, b, c，则可计算出他们的隶属度，分别为 μ1(a)，μ2(a)，μ1(b)，μ2(b)，μ1(c)，μ2(c)（μ1、μ2分别表示与查询数据相对应的两个隶属度）。此时，每个参数所对应语言值便组成了需要利用的模糊规则的前件集合。前件参数有三个，每个参数有两个语言值，则可对应8条不同的模糊规则。这些规则的结论（即Y1～Y4的语言值），可以在规则库中查询出来。

与此同时，系统还需要计算该数据组与规则对应的确定度。此确定度的定义一般有两种方式：1）用隶属度的最小值来表示；2）用隶属度的乘积表示。则对于上述8条规则的第一条，若用β来表示确定度，可表示为 β1=min[μ1(a) , μ1(b), μ1(c)]，或β1=m1(a)×m1(b)×m1(c)。本文采用了第一种方法。

解模糊的过程使用了重心法。如图3所示，在此输出隶属度函数曲线中，每个梯形的高度，就是此语言值所对应规则的确定度，整个阴影区域组成图形的重心就是精确值所在的坐标位置。

图3 重心法

若用ki表示规则i结论隶属函数的中心，用βi表示隶属函数曲线下的面积，则精确值u的计算式即为：

根据式（2）的计算方法可以将模糊的推理结果解模糊化为精确量，即得到砂轮转速、工件转速、背吃刀量和中径余量的工艺参数参考值。

4 实验验证

为了验证本文所述方法的有效性，本文将200组案例数据输入系统进行学习，并给定一系列加工要求，对其进行模糊推理，得到工艺参数。将这些参数与加工过程中实际使用的工艺参数进行比较，结果如表2所示。

表2 实验结果

该实验结果表明，使用本文所述方法所推理出的工艺参数符合实际加工所需的精度要求，能够为螺纹磨削加工工艺参数的确定提供有效的参考。

5 结束语

由于螺纹磨削加工工艺的复杂性，普通的磨削数据库系统很难对此种加工的工艺参数确定起到很好的指导作用。本文以技术人员在实际加工过程中的数据作为基础，自行学习产生模糊规则库，并最终通过模糊推理算法完成对加工工艺参数的推荐，保证推理结果可靠有效的同时，便于加工企业在实际生产过程中的使用，是解决加工工艺对实际经验依赖性问题的一个有效方法。此外，由于对输入输出参数的数量和类型没有严格的限制，该方法还具有一定的通用性，能够在其他机械加工的工艺制定过程中发挥同样的作用。

[1]曹甜东, 盛永华. 磨削工艺技术[M]. 沈阳: 辽宁科学技术出版社, 2009.

[2]王先逵. 螺纹加工[M]. 北京: 机械工业出版社, 2008.

[3]易继锴, 侯媛彬. 智能控制技术[M]. 北京: 北京工业大学出版社, 1999.

[4]Thomas Sudkamp. Interpolation, completion, and learning fuzzy rules[J]. IEEE Transaction on Systems, Man, And Cybernetics, 1994, 24(2): 332-341.

[5]黄黎明, 唐朝晖. 智能控制过程中模糊专家控制规则的获取[J].计算机工程与应用, 2007, 43(13): 239-242.

[6]K. Hashmi, M.A. El Baradie, M. Ryan. Fuzzy-logic based intelligent selection of machining parameters[J]. Journal of Materials Processing Technology, 1999, 94: 94-111.

[7]师黎, 等. 智能控制理论及应用[M]. 北京: 清华大学出版社, 2009.