细致观察，寻找二元一次方程组的特殊解法

☉江苏苏州市苏州工业园区第十中学 潘卫峰

细致观察，寻找二元一次方程组的特殊解法

☉江苏苏州市苏州工业园区第十中学 潘卫峰

心理学上认为观察是一种有目的、有计划、主动并有思维参与的知觉过程.数学观察能力是指利用视觉感官高效地提取信息，并调动各种数学思维和储备知识对信息进行提炼、加工，构建数学模型，最终利用数学知识进行解决问题的能力.迅速而有目的、细心的观察能力，是数学其他能力发展的基础，也是有效开展数学活动的重要前提.解二元一次方程组，除熟练代入消元法和加减消元法外，还应根据方程组的特征，通过细致观察题目的一些特征，灵活运用一些特殊方法，这样既可使解题过程简洁明快，又能提高应变能力和学生的创造能力，现举例说明.

一、整体代入法

整体代入法是数学学习的重要方法，它的技巧在于把这个式子整体看做一个数或者是一个整体，求解时只要把整个式子的值求出即可，既方便又简化计算.

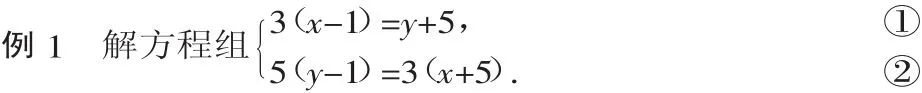
分析：注意到方程①的左边可化为 3（x+5）-18，把 3（x+5）看成一个整体代入，从而简化过程.

二、整体加减法

整体加减法是将方程的两个等式的左边和左边相加，右边和右边相加，可以简化未知数的系数，便于计算.

分析：因为方程①和方程②的未知系数正好对调，因此可采用两个方程整体相加或相减求解.

三、换元代入法

通过观察可以知道两个方程的某一部分相同，可以用一个或两个字母来代替方程中的式子，先解出字母的值，然后将字母的值再代入式子中，求出未知数的值.这种方法可以将繁杂的式子先简单化，避免计算的复杂性.

分析：观察发现这两个方程的左边两个式子相同，可以直接用换元法换掉相同的式子.

四、参数代入法

有时候方程组中的一个方程只是比例式，可以引进一个参数，令这个比例式等于这个参数，利用这个参数来表示这两个未知数，然后代入另外一个方程中，先求出这个参数的值，就可以求出这个方程组的解了，这种方法应用起来比较简便.

分析：通过观察发现①式是比例式，可以直接令①式等于一个参数，表示出两个未知量，然后代入②式求解即可.

五、消去常数法

这种方法是将常数消掉，或者代换掉，得到一个没有常数项的方程，就可以得到两个未知数之间的倍数关系，然后再代入任意一个方程，求解出方程组的解.

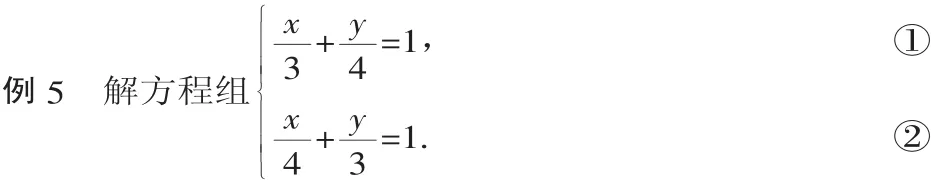
分析：通过观察，发现两个方程的右边的常数相等，左边没有常数，所以把常数消掉后只剩下两个未知量的倍数关系，然后代入求解即可.

通过以上列举的例子可以看出，观察能力的培养必须落实于具体的教学过程中，在日常的授课中培养学生的能力.这就需要教师精心组织课堂教学，大胆放手给学生，通过操作、观察、实验、猜想、验证等一系列的思维活动，使学生的能力得到全面的发展.数学观察能力是学生其他能力发展的基础，观察能力的培养需要通过具体的教学活动来实现.可以说，细致观察题目，是做对题目的第一步，也是关键的一步.