例析“三线”问题中的数学思想
2012-08-25江苏高邮市龙虬初中王麦香
☉江苏高邮市龙虬初中 王麦香
例析“三线”问题中的数学思想
☉江苏高邮市龙虬初中 王麦香
“三线”(线段、射线、直线)是最基本的几何图形,是学好几何知识的重要基础,它们的应用十分广泛,对于初学者来说也是一个难点.因此同学们在学习时,不仅要理解概念,灵活运用,还应当体会其中所蕴含的数学思想方法.
一、数形结合思想
例1 在数轴上的点A、B位置如图1所示,则线段AB的长度为( ).

图1
A.-3 B.5 C.6 D.7
解:线段AB的长度就是点A与点B分别到原点的距离之和,即2的绝对值与-5的绝对值之和,故答案选D.
评注:这道例题既考查了线段的和、差关系,又反映数轴与绝对值的几何意义,充分体现了数形结合的思想.
二、分类讨论思想
例2 已知线段AB=8cm,在直线AB上有一点C,且BC=4cm,M是线段AC的中点,求线段AM的长.

评注:分类讨论思想方法是初中数学的重要内容,漏掉第二解是本题最容易出错的地方,要全面考虑C点是在线段AB上,还是在AB的延长线上,对所出现的位置关系进行讨论.同时要认识到本题最根本的错因是未分清“线段AB”和“直线AB”两个概念,因此,同学们今后要在基本概念的准确性上下功夫.
三、转化思想
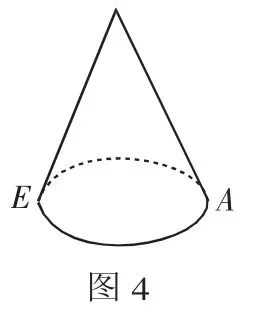
例3 如图4,是一个用来盛爆米花的圆锥形纸杯,在A处有一块爆米花残渣,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点.请你结合圆锥的侧面展开图,设计一条最短路线.
解:将圆锥体的侧面的展开如图5所示,点A是弧线的中点,连接EA,那么线段EA就是蚂蚁爬行的最短路线.

评注:在立体图形中研究两点之间的最短路径时,通常把立体图形的表面展开,转化为平面图形中的两点间的距离问题.
四、归纳思想
例4如图6所示.(1)当直线上有4个点时,数一数共有几条不同的线段.(2)当直线上有n个点时,想一想共有几条不同的线段.
解:(1)图中有6条线段,按照一定顺序依次数,分别是线段AC、线段AD、线段AB、线段CD、线段CB、线段DB.

图6

评注:本题要按照一定的顺序进行计数,要求做到不能重复和漏数,找出计数的规律,归纳出计数公式,这个公式同样适用于数角、数交点等等,同学们不妨试试.
五、方程思想
例5 如图7,B、C两点把线段AD分成2∶3∶4三部分,M是线段AD的中点,CD=8,求MC的长.

图7

评注:本题在求解线段的长度时,通过设出未知数,根据已知与未知之间的等量关系,用方程解决问题,体现了方程的思想.使实际问题方程化,这一思想方法是初中数学常用方法,同学们在今后的学习中将渐渐体会到.
