学生学习中使用几何画板提升探究能力的实践研究

☉上海市老港中学 王元友

学生学习中使用几何画板提升探究能力的实践研究

☉上海市老港中学 王元友

上海市第二期数学课程改革让学生的数学学习方式发生了根本性转变，其目的在于构建一种自主合作、探究式的学习方式.在二期课改理念的指引下，基于提升学生的探究能力，笔者向上海市浦东新区教科研室申报了课题《学生学习中运用几何画板提升学生探究能力的实践研究》，并且引导学生在数学学习中运用几何画板对部分函数的性质、图形运动中的不变性进行了实践研究，下面将部分研究成果与同行们分享.

一、利用几何画板探索函数的性质，体会数与形变化的内在联系

函数的图像与性质是初中阶段教学的重点和难点，利用几何画板探索其图像及性质的形成过程，使学生经历从特殊到一般的认识过程，体验知识产生、发展、形成的过程，逐步培养学生抽象概括能力，激发学生求知的欲望.

案例一：二次函数图形形状、性质的探究

函数是研究运动变化的重要数学模型，函数概念的实质就是运动变化与联系对应.几何画板在这一方面具有独到的优势，利用它作图可以动态地表现图像的变化过程，满足数学教学中化抽象为形象直观的要求.函数的图像采用描点法，锻炼了学生的动手能力，让学生亲历实践过程，解决了学生刚接触函数通常作图的几个误区：取点过少、取点不具有代表性、描点不准确，描出图像不光滑、对无数个点和无限延伸难以理解.利用几何画板绘制函数图像，通过追踪点得到函数图像的踪迹动画，通过运动点让学生清楚看到点动成线的动态过程.下面以二次函数图像的绘制过程为例说明学生学习中使用几何画板的过程.

作出 y=0.3（x-1.00）2-5.0 的图像.

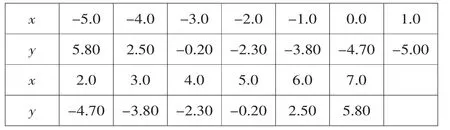
如图学生通过《几何画板》只需拖动填表、描点、连线所对应的手型图，即可完成列表、描点、连线等过程，绘制出给定的二次函数的图像；而改变a、h、k的值，即可归纳总结出a的符号决定二次函数的开口方向和大小，h的值决定对称轴的位置，h，k的值决定顶点的位置等.经历这样的学习过程，学生学习的兴趣浓厚了，进一步掌握了二次函数的图像特征，对二次函数及函数的本质理解更深.

案例二：二次函数图形运动规律的探究

在“二次函数y=ax2+bx+c（a≠0）的图像”一节中，如何向学生说明y=ax2、y=ax2+c、y=a（x-m）2、y=a（x-m）2+c等4个特殊的二次函数图像的性质及相互关系一直是传统教学中的重点和难点，学生难以理解，教师也难以用文字语言说明.让学生自己利用《几何画板》进行探究性学习，如图通过《几何画板》只需用鼠标上下拖动点改变a、h、k的值，即可获得y=ax2、y=ax2+c、y=a（x-m）2、y=a（x-m）2+c等函数图像和性质，在a、h、k的变化过程中进一步体会到a、h、k的大小对于二次函数图像的形状的影响，加深对二次函数的性质的理解.并且拖动点M，利用《几何画板》反复动态演示y=ax2、y=ax2+c、y=a（x-m）2、y=a（x-m）2+c等函数图像的相互变换，学生便可比较顺利地掌握二次函数的图像平移规律的知识难点，归纳总结二次函数的平移规律：上加下减、左加右减.如图2进一步引导学生拖动点W，还可以演示二次函数都是轴对称图形这个对称性规律，类似的我们还可以引导学生归纳二次函数旋转与翻折的规律.

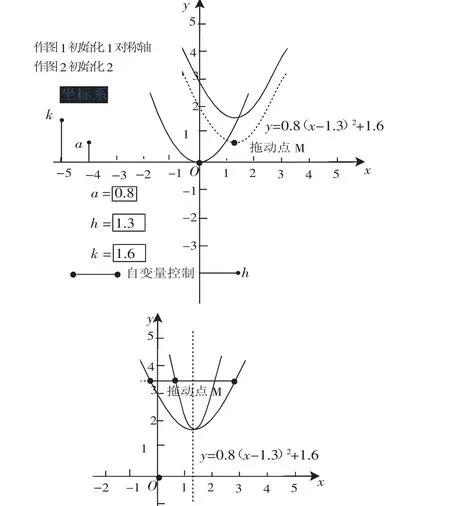
类似的，初中阶段的其他函数如正比例函数、一次函数、反比例函数的图像、性质均可以采用类似的学生学习中自主运用几何画板进而总结它的图像、性质等规律.

学生学习中运用几何画板的实践操作，可以让学生在实践中感知，让学生通过自己的努力解决问题获取知识，教师再引导学生到实际中验证.这样，学生对知识就会有更深入的理解，探究能力得到进一步提升.

二、利用几何画板探索图形运动过程中的变与不变性

学生在数学学习中，运用几何画板感受到数学知识的发现过程，进而在已有的知识上猜想结论，发现定理，可以提升学生的探究能力，感受到图形运动过程中的变与不变性.

案例三：三角形内角和定理的发现过程

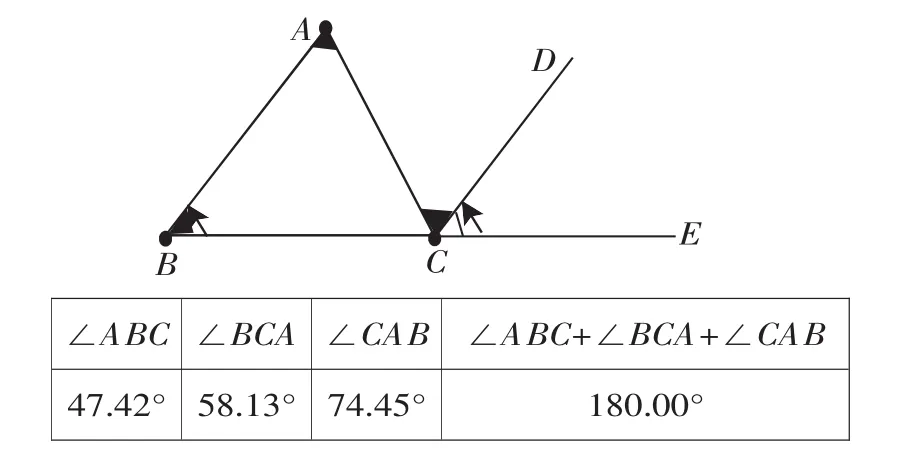
如在“三角形内角和为180°”的定理的讲解过程中，不是直接证明定理，而是结合《几何画板》中的角的度量的功能，让学生随意画一个三角形，度量出每一个角的大小，求出三个角的和，猜想出三角形内角和为180°这一命题，再让学生自己拖动点A、B、C去感悟：点A、B、C运动过程中变化的是∠ABC，∠BAC，∠ACB的大小，不变的是ΔABC的内角和的度数，永远为180°，然后再用平行线知识去证明.这样的实践，首先学生情感上容易接受这一知识点，其次体现了数学前后知识的联系，最重要的是，学生运用几何画板的度量功能快速提升了他们的探究能力，即直接发现结论的能力.

案例四：中点四边形的再探究

“顺次连接四边形（或平行四边形、矩形、菱形、正方形、等腰梯形）各边中点所得的四边形是什么形？”这是一道常见的探究性题目，很多用传统方法来讲，要在黑板上画出大量图形，而且很难讲清楚.基于本题的探究性较强的特征，故制作了几何画板课件，动态地展示了当四边形变为“平行四边形、矩形、菱形、正方形、等腰梯形”时，顺次连接四边形（或平行四边形、矩形、菱形、正方形、等腰梯形）各边中点所得的四边形的变化情况，学生很容易发现其变化的本质进而总结了规律：任意四边形的中点四边形是平行四边形，对角线相等的四边形的中点四边形是菱形，对角线垂直的四边形的中点四边形是矩形，对角线垂直且相等的四边形的中点四边形是正方形.

又如三角形中位线的学习过程，画出一个三角形的中位线后，利用度量功能，量出中位线与第三边的长度，比较数据后得出“三角形的中位线等于第三边的一半”这个结论，使学生觉得心服口服.有学生甚至把我的课件拷回家自己研究，实验，得出了相同的结论，既提高了自己的动手能力，又增加了学习数学的兴趣.几何画板的动态性，可以让学生获得真正的数学经验，而不是数学结论.

学生利用《几何画板》工具把静态的知识动态化，抽象的知识具体化，亲身体验，自主探索，在学中尝试，在尝试中学，激发创新思维，提升了思维活动的层次，培养了数学学习的基本素质.

《数学课程标准》指出：要让学生亲历数学知识的形成过程.只有学生通过自己的亲身感受、自我探索获得的知识，才会根深蒂固地扎根在脑海中.“学生学习中使用几何画板”的核心就是由学生本人把要学的东西自己发现和创造出来，这样可以激发学生的学习兴趣，获得知识，理解概念，探求规律与方法，提升自己的探究能力，尤其是解题的能力.