在解题教学中培养学生的创新思维

2012-08-25江苏兴化市教育局教研室陈德前

中学数学杂志 2012年2期

☉江苏兴化市教育局教研室陈德前

在解题教学中培养学生的创新思维

☉江苏兴化市教育局教研室陈德前

陈德前，男，1957年生，江苏省兴化市教育局教研室副主任，泰州市教育局教研室兼职教研员，中学高级教师，江苏省中学数学特级老师，泰州市有突出贡献的中青年专家，泰州市初中数学名师工作室的领衔人，发表文章百余篇，出版书籍20多本.

《义务教育数学课程标准》要求：“通过义务教育阶段的数学学习，学生能够具有初步的创新精神和实践能力，在情感态度和一般能力方面都能得到充分发展.”可见，创新能力的培养是新课程理念的重中之重.要培养学生的创新能力，就要在教学过程中培养学生创造性地运用知识去解决问题的能力，其核心就是培养学生的创新精神和创新思维.创新精神是指能敏锐地把握机会，并勇于付诸探索实践的精神状态.创新思维是指个人在头脑中发现事物之间的新关系、新联系或新答案，用以组织某种活动或解决某种问题的思维过程.创新思维对于完成创造性活动，培养创新型人才是不可缺少的心理因素.因此，在学校的教育教学工作中，应十分重视学生创新思维的培养，要把它贯穿到每一个环节中.那么，作为一名数学教师，怎样在解题教学中培养学生的创新思维呢？下面结合本人的教学实践，谈几点体会，供研讨.

一、标新立异是培养创新思维的前提

创新思维具有异常、新奇的特点，它不完全依赖于逻辑思维，必须发挥标新立异的想象能力.因此，要培养学生的创新思维，在数学解题教学中，就要求教师尊重学生的创新精神，注意引导学生克服思维定势，鼓励他们在解题时敢于打破常规，不受传统解法限制，大胆地多方向地想象，以训练思维的灵活性，培养思维的跳跃性.当学生思维受定势干扰时，可让学生说出他们是用什么方法去解决的，为什么，再启发他们想想看有没有其他办法；如学生实在想不出来，教师可以指出定势干扰在哪些方面，让学生自己克服，从而使学生顺利地向新的方向探索，创造性地解决问题.

例1 李明与王云分别从A、B两地相向而行,若两人同时出发,则经过80分钟两人相遇；如李明出发60分钟后王云再出发,则经过40分钟两人相遇.问李明与王云单独走完AB全程各需要多少小时.

本题中的数量关系比较复杂,绝大多数学生都是通过设辅助未知数列方程组来求解的，比较复杂，也有部分学生束手无策.在学生思考讨论发言后，教师清楚了产生问题的根源是思维受定势干扰，其实题目中并未有此要求.此时应启发学生另辟蹊径,寻求更简便的解法，鼓励他们不为陈规所局限，善于变通、立异，勇于突破，并启发他们：由题知,第一种情况两人各用了80分钟；第二种情况李明用了100分钟,王云用了40分钟,都走完了全程.从中你可以发现什么结论？由此你可以得到本题的简洁解法吗？学生经过小组讨论，不难发现结论：李明走20分钟所走的路程相当于王云走 40分钟所走的路程.于是简洁解法应运而生：在第一种情况里,王云走的80分钟路程李明要走40分钟,因而李明走完全程共需120分钟即2小时；李明走 80分钟的路程王云要走160分钟,因而王云走完全程共需240分钟即4小时.这样口算即可得到结果,多么的简洁，充分说明了创造性思维的巨大威力！

例2 如果y=（x-1）a2+3a在0≤x≤1时永远是正数，求a的取值范围.

本题学生初看后都感到很棘手，与他们交流后发现：他们都是从a为主元，y=（x-1）a2+3a是关于a的二次函数这个角度（思维定势）来考虑的.发现问题的症结后，教师启发学生：a一定是自变量吗？可否换个角度，变通一下自变量，得到一次函数呢？学生很快发现，x也可以为自变量，从而稍作变形即可得到关于x的一次函数y=a2x+（3a-a2），它的图像是一条直线，要使函数值在0≤x≤1时永远是正数，只要保证在x=0和x=1时y的值是正数即可以了.当 x=0 时，y=3a-a2；当 x=1 时，y=3a.因此有 3a＞0且 3a-a2＞0，解得 0＜a＜3，这就是要求的 a 的取值范围.真是变一变，天地宽.

二、多向发散是培养创新思维的核心

心理学告诉我们：“集中型思维和发散型思维是构成创造性思维的必要成分.对创造性思维来说，两者缺一不可.但是，在创造性思维的形成过程和发展中，培养发散型思维尤为重要.”因此，我们在解题教学中，应多设计一些开放性的题目，引导学生经常进行“一题多解”的练习，给学生提供一个能够充分表现个性，激励创新的空间，培养学生的发散思维.

例 3 如图 1，∠BAC=∠ABD，∠C=∠D，求证：OC=OD.

这是一道基础题，一般学生都能解决，且解法不唯一，是进行“一题多解”，培养发散思维的好题.在教学中，可先让学生自主探究，然后合作交流.合作交流与自主探究是相辅相成的，有助于培养学生的创新意识和创新能力.在合作学习的过程中，有助于学生摆脱以自我为中心的思维倾向，能把各自的想法、思路更好地表现出来.在相互讨论的过程中，又有助于激发新的灵感，提出新的设想.但仅仅是满足于以上的教学是不够的，还可以将题目进行改编，从解法上的“一题多解”到题目条件或结论的“一题多解”，这样不仅拓宽了学生的解题思路，而且还能有效地培养学生的创新思维.如：

（2010年甘肃省中考题）如图1，∠BAC=∠ABD.

（1）要使OC=OD，可以添加的条件为：______或______；

（2）请选择（1）中你所添加的一个条件，证明OC=OD.

例4 写出一个解集是x＞2的不等式：________.

三、广泛联想是培养创新思维的重要途径

数学中“由此及彼”的联想能力在培养创新思维的活动中有着十分重要的作用，许多科学家的重大发明都是广泛联想的结果.伽利略看到人们推车后，从反面提出问题：“如果不用力，车子会怎样？”从而发现了惯性；鲁班被齿叶划破了手和衣服，却从中受到启发，发明了锯子.前者是发现一种现象后，立即联想到它的反面，这种联想叫做思维的逆向联想；后者是发现了一种现象后，立即联想到与它相似的其他现象，这种联想叫做思维的横向联想.它们与思维的正向联想、纵向联想称之为思维的四种联想形式.从“创新”的角度来看，思维的逆向联想和横向联想的培养更值得重视.

例 5 已知方程 A：x2+4mx+3-4m=0，B：x2+（m-1）x+m2=0，C：x2+2mx-2m=0中至少有一个方程有实数根，求m的取值范围.

例 6 若（x-z）2-4（x-y）（y-z）=0，试求 x+z与 y的关系.

四、综合应用是培养创新思维的关键

心理学告诉我们：“灵感的形成是创造性思维的关键”.而灵感的形成不仅要靠精密的观察、丰富的想象，而且要对一个问题拥有足够的资料，要能把代数、几何、三角，概念与运算，理论与实际，数与形，知识与技能，过程与方法等综合渗透，解题时注意综合应用，做到融会贯通，只有这样，才能做到创造性解题，从而达到培养创新思维的目的.

例7（2009年甘肃省庆阳中考题）如图2，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地.若耕地面积需要551m2，则修建的路宽应为（）.

A.1m B.1.5m

C.2m D.2.5m

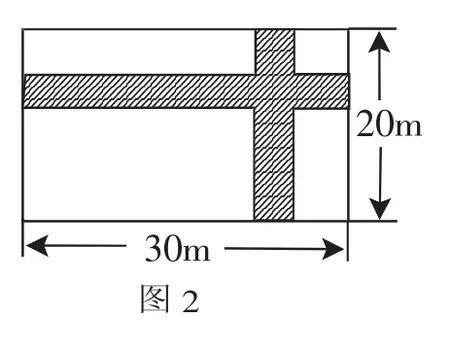
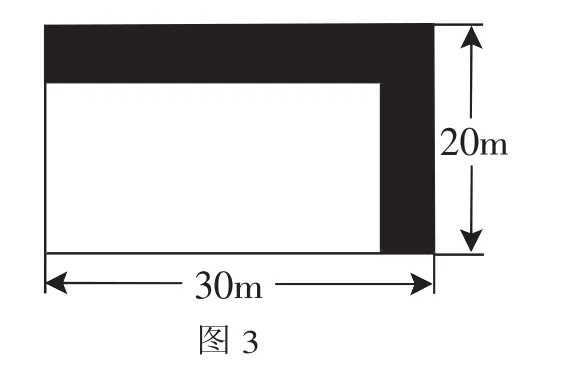
解析：本题的一般解法是设修建的路宽应为xm，从矩形总面积中减去两条道路的面积，得到方程：30 ×20-［30x+（20-x）x］=551，解得x=1，选A.有些考生重复减去交叉部分的面积，得到30×20-30x-20x=551的错误方程.为了减少这种错误，可以考虑特殊图形——利用平移的方法将它转化为规则图形来思考：由题意转化为图3，设道路宽为xm，根据题意，可列出方程，（30-x）（20-x）=551，整理得x2-50x+49=0，解得 x1=49（舍去），x2=1.所以道路宽为1m，选A.这里在解决实际问题应用题时，灵活应用了几何中平移的知识，化难为易，化繁为简，创造性地解决了问题.

例 8 在△ABC中，a、b、c是三角形的三边，求证：a2+b2-2abcos（C+60°）=b2+c2-2bccos（A+60°）=c2+a2-2cacos（B+60°）.

本题是研究△ABC的边与角之间的数量关系的，在教学中，可以引导学生充分观察问题的结构特征、数量特征，即可发现：问题的结论形式与余弦定理较接近，只是三个角是原三角形的各个角加上60°，由三个60°的角联想到等边三角形，就可以构造出如图4所示的图形，这样学生就可以创造性地运用图形来巧妙地解决这个问题.

由本例可见，数形结合所产生的“速效”与“高能”的作用甚为巨大！

简证：以△ABC的边AB、AC为边向形外作等边三角形ABD、ACE，则易证△ABD≌△ACE（SAS），所以 BE=CD.再在△ABE、△BCD、△BCE中运用余弦定理即可得到结论.

数学课堂解题教学中对学生创新思维的培养，需要教师以现代教育教学理论为指导，综观全局，充分协调教学中的各种因素，创设民主氛围，确保学生心理自由，采取教学技法，激活思维能力，运用人格力量，弘扬学生个性.惟有如此，学生的创新思维之花，才能在数学课堂教学这块沃土上结出丰硕之果.