乘法公式在初中数学知识中的几种应用

☉江苏沭阳县实验中学 胡会侠

乘法公式在初中数学知识中的几种应用

☉江苏沭阳县实验中学 胡会侠

乘法公式包含两个运算公式，即平方差公式、完全平方公式，是初中数学学习中最基本的、应用最广泛的公式，同时也是初中中考命题中比较重要的考点之一，灵活巧妙地应用乘法公式可以使计算过程简捷方便，达到事半功倍的效果，现分析乘法公式在初中数学中的五个重要的应用.

一、乘法公式在解方程或不等式组中的应用

例 1 解方程：（2x+3）（2x-3）+3（x+2）（x-2）=（x+1）（7x-1）.

分析：先利用平方差公式和，再利用多项式乘法法则展开，按照解方程的步骤即可求解.

所以不等式组的解集为（5，+∞）.

二、利用乘法公式简算

例 3 计算：3×（22+1）×（24+1）×（28+1）×（216+1）+1.

分析：计算 3×（22+1）×（24+1）×（28+1）×（216+1）时可知直接计算比较烦琐，而且数字较大，不易计算，尤其是最后的乘积.但发现3=22-1，可将原式变形为含有平方差公式的计算式.

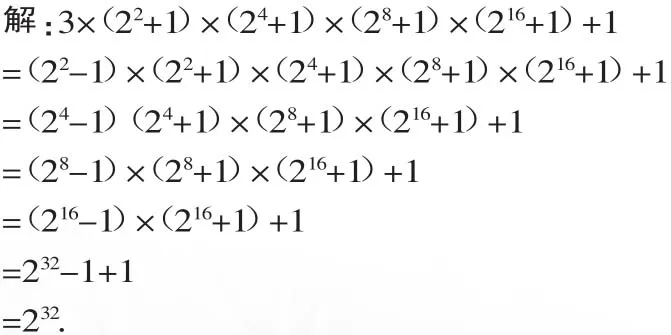
三、完全平方公式在三角形中的运用

例4 已知：△ABC的三边长分别为a、b、c，三边满足a2+b2+c2-ab-bc-ac=0的关系式，试判断△ABC的形状并说明理由.

分析：关系式a2+b2+c2-ab-bc-ac=0体现了△ABC三边长之间关系，从关系式形式上与完全平方公式很相近，只是相差2ab和2bc与2ac中的2倍，利用等式性质可转化为2a2+2b2+2c2-2ab-2bc-2ac=0即可.

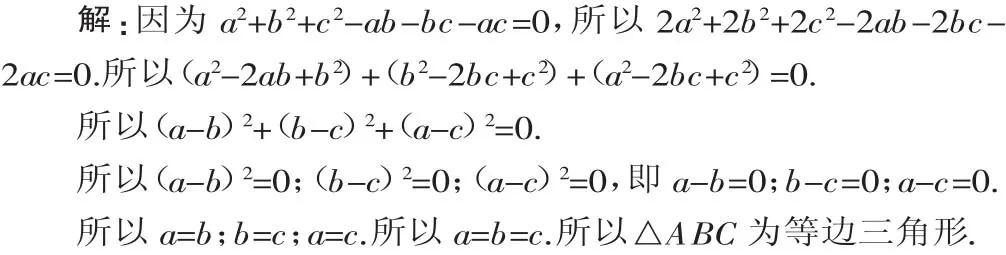
四、利用乘法公式证明

例 5 证明：对于任意整数 n，整式（2n+1）2-（2n-1）2-8是 8的倍数.

分析：要判断整式（2n+1）2-（2n-1）2是 8 的倍数，只要最后的结果中会有8的因数.

证明：（2n+1）2-（2n-1）2-8=［（2n+1）+（2n-1）］［（2n+1）-（2n-1）］-8=4n×2-8=8（n-1）.

又因为n是整数，所以n-1是整数，可得8（n-1）是8的倍数.

五、利用乘法公式变形求值

例 6 已知：（a+b）2=8；（a-b）2=4，求 a2+b2及 ab 的值.

分析：（a+b）2和（a-b）2的展开式中都含有 a2+b2及 ab，因此将（a+b）2=8、（a-b）2=4 展开，把两个等式看成关于 a2+b2及 ab 的方程组，解方程组即可.

乘法公式除了以上知识点，也涉及很多知识，常常融入到其他知识综合题中，在数的运算、代数式的化简、解方程等方面都有极其广泛的应用，但要记清这些公式的结构特点，以便能够举一反三，触类旁通，总结规律，真正培养学生的求异思维和类比思想，提高知识水平、运算能力以及对知识的贯通能力.