重视数学体验构建高效课堂

2012-08-25江苏姜堰市励才实验学校肖维松

中学数学杂志 2012年2期

☉江苏姜堰市励才实验学校肖维松

重视数学体验构建高效课堂

☉江苏姜堰市励才实验学校肖维松

现代数学教学强调对数学问题本质的体现和过程的揭示.数学课程标准指出：数学课程应力求通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程，发展他们的创新意识.现在倡导的自主学习、探究学习和研究性学习，正是使学生得到数学体验、将隐性知识逐渐显化的好途径.它们的一个共同特征就是强调学生的亲历亲为，强调学生的独特体验.只有学生亲自参与获取知识的过程，才能体验求知的快乐，才能真正激发其学习兴趣，提高课堂教学实效.所以在课堂教学中，需要我们研究和思考：在课堂教学中能否让学生多一些探究结论、发现问题的体验，创设开放、互动、新型的数学体验环境？

1.重视引导阅读，在与教材对话中体验

新课程的实施改变了老师的教学习惯，为教学带来了新的气象，教师在教学中还存在满堂灌现象，对教材的重视不够，缺乏对阅读的有效指导，使学生丧失了体验教材的机会，造成学生中存在概念不清、公式不明、生搬硬套、解题不规范等不良现象.其实，阅读是最好的老师，是最有生命力的学习方法，真正有效的阅读可以让学生真切地感受到数学知识的延续、方法的美妙，进而探求隐含在作品中的数学思想；通过阅读可以培养学生对数学语言的感悟能力，从而提高数学表达水平，进一步领悟其中蕴含的数学思想方法.

我们在课堂教学中，强调“文字语言”、“数学符号语言”、“图形图表语言”之间转换的重要性，尽可能地将数学文字全部用数学符号和图形来表达，实现互译甚至是意译.当学习者能进行此种转换，并能自如运用数学符号语言进行表达时，学习者对知识的理解更透彻.

案例1：在研究苏教版二次函数y=a（x+m）2+n（a≠0）的图像和性质时，可以指导学生阅读教材，解答下列问题.

问题1：分别说出函数y=ax2（a≠0），y=ax2+n（a≠0），y=a（x+m）2（a≠0）的图像和性质.

问题2：指出它们图像和性质的联系.

问题3：你能确定二次函数y=a（x+m）2+n（a≠0）的图像和性质吗？

通过对教材的阅读，进一步认识二次函数图像和性质，体验到“从特殊到一般”、“数形结合”等一般性的数学研究方法，以及概念用词的凝炼.让学生通过阅读和对比感悟二次函数：y=ax2（a≠0），y=ax2+n（a≠0），y=a（x+m）2+n（a≠0）的图像和性质的区别与联系.特别是图像的平移的方法.这比许多教师直接给出结论，告诉学生，没有让学在实例与概念的阅读对比中获得，更使学生理解深刻.

2.重现创设情境，在探究过程中体验

数学是思维的科学.数学学习不是简单的“告诉”，而应是学生个性化的“体验”.数学课堂“问题情境”的创设直接影响学生的数学体验.教师要善于创设针对性强和适合学生的体验情境，诱发学生内在的认知冲突，激发学生的思维，唤起学生的丰富想象，让知识经历一个再发现、再创造的过程，从而让学生体验到知识形成过程，感受到过程中所涉及的思维策略，促进对所学内容的深刻理解.

案例2：在研究“三角形内角和定理”时，可采取从特殊到一般的方法.

首先，由一副三角板和正三角形的三个角，引导学生发现它们共同具有的属性：90°+60°+30°=180°，90°+45°×2=180°，60°×3=180°.

其次，提出问题：“任意的一个三角形的三个角都有这种关系吗？”让学生任意画一个三角形，用量角器量一量并列出表1，发现三个角之和都等于或接近，并追问：“为什么是接近180°？”（测量会产生误差），从而得到定理的结论.

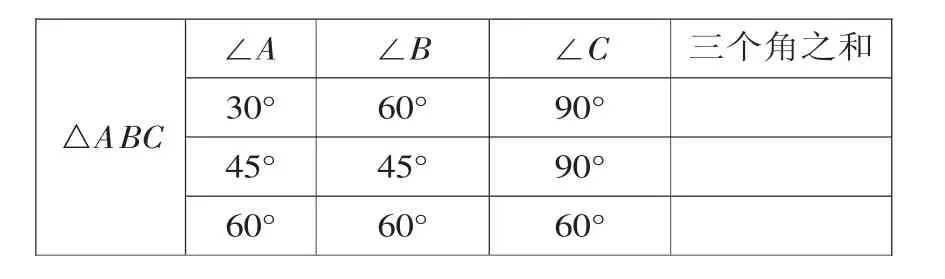
表1：

最后，在证明定理时，从结论入手，提出一系列有针对性、启发性的问题引导学生进行联想.

师：180°与学过的哪些知识有关？

生1：平角、邻补角、平行线的一组同旁内角.

师：怎样证明三角形三个角之和等于平角？

生2：保持一个角不动，将另两个角移过来.

师：怎样制造同旁内角互补？

生3：作平行线.

学生边思考，边动手画图尝试，得出多种证明方法（如图1所示）.

图1

施教之功，贵在引导，学生是学习、认识、发展的主体.正如每个人都只能用自己的器官吸收营养一样，学生也只能用自己的“器官”吸收知识的能量.教师引导学生自主探究、尝试、获取知识，才能真正实现教学的有效性.

3.重视动手实践，在实践中亲身体验

学生有目的地动手实践，亲身参与探究活动是数学体验的主要途径.既能深化所学课内知识，提升数学体验，又能培养学生的实践能力，更重要的是经过亲身实践获得的数学体验，远比目睹幻灯片播放更能“体验数学发现和创造的历程”.在逼真的问题情境中展开自主探究，展示了学生的数学才华，提高了应用数学的技能，使抽象的数学知识直观显示.

案例3：在研究反比例函数的图像及其性质时，传统教学的难点有两个：一是双曲线的形成，二是对双曲线与两坐标轴无限逼近的理解.为了突破这两个难点，改变“传统的教师示范—学生模仿、练习”的教学模式，把学生带进计算机教室，并为他们提供一个画图软件，然后让学生利用这一多媒体技术，在教师的指导和帮助下，通过给自变量赋与许多的不同数值，让学生自己来“绘制”双曲线，并最终发现并归纳出反比例函数的图像及其性质.

这样的数学活动，不是独立地理解数与形，而是自然而然地由数到形，学生加深了对反比例函数的图像与性质的理解与掌握.

4.重视合作交流，在思维碰撞中体验

数学课程应倡导自主探索、动手实践、合作交流、阅读自学等学习方式，在独立思考的基础上进行合作交流，在思考、探索和交流的过程中获得对数学较为全面的体验和理解.特别是对数学的易错点或探究点，采用与他人交流合作等学习形式，往往可引起学生产生积极的认知变化和深刻的数学体验.

案例4：在九年级学生学习完“一元二次方程”后的一堂复习课上出示这样一道练习题：

已知关于x的方程（3k+1）x2-2-1=0有两个不相等的实数根，求k的取值范围.

问题提出后，学生的思维很快打开.

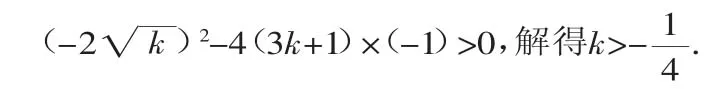
听完学生的分析，教师并没有指责他们，而是笑了笑，说：有没有同学要补充？

经教师的提醒，生2补充：此方程是一元二次方程，故还必须保证二次项系数3k+1≠0，即k≠-.故k的取值范围为k＞-，且k≠-.

这时，生3举手说：生2的分析是对的，但结论还是不对，因为k≠-不在k＞-的范围内，因此k的取值范围还是k＞-.

教师立即表示有道理，继续问：还有陷阱吗？

课堂顿时活跃起来，学生你一言我一语，纷纷发表自己的见解.过了一会儿，教室内传来几位同学的声音：哎呀，被开方数k要大于0呀！

教师对其加以肯定，并让其中的生4发言.

4题最终k的取值范围是k≥0.

学习是一个认知过程，这个过程通过合作、交流、学习易产生突然的“顿悟”.合作学习的效果不能用当堂的课堂教学效益来衡量，而要看这个问题在实施中能否最大程度地激发学生的数学体验，能否促进学生对问题进行重新思考，能否让学生更深入地挖掘出问题的内涵.理想的课堂是真实的课堂，课堂上经常会有学生回答错误或理解错误.教师不要急于求成，把错误的事实转化为探究问题的情境，在错误处敲打磨练，引导学生思索，不但能发现和解决问题，而且能使学生获得在一般情况下所没有的感知和体验，既感到知识的魅力，又感受到学习的快乐.

5.重视题目变式，深化数学体验

数学学习是一个动态的过程.我们常发现学生的解题能力不强，对一个在新情境下略微变化或引申的问题常常束手无策.这主要因为老师在数学中提供给学生的往往是封闭的问题和固定的思路，把自己的体验强加给学生，没有让学生体验数学的发现和创造的历程，发展他们的创新意识，题组教学或变式教学是改变这种现状的一个有效途径.通过几个问题的前后联系及解决这些问题的方法变化，或有目的、有计划地对教学内容进行适当变化，形成一种更高层次的思维方法，以达到对问题本质的理解、规律的掌握、技能的巩固、思维的拓展与迁移目的，从而揭示不同知识间的内在联系.

案例5：在研究概率时，出示一组问题：（1）连掷两枚骰子，它们的点数相同的概率是多少？

（2）转动如图2所示的转盘两次，两次所得颜色相同的概率是多少？

（3）某口袋里放有编号1～6的6球，先从中摸出一球，将它放回到口袋中，再摸一次，两次摸到的球相同的概率是多少？

（4）利用计算器产生1～6的随机数（整数），连续两次随机数相同的概率是多少？

通过题组教学或变式教学，让学生体验到看不到的东西，本案例的四个小题具有相同的数学模型，旨在通过多题一解，让学生体会到它们是同一数学模型，体验到数学思想方法.它从数学的一个基本问题出发，进行类比、联想、特殊化和有度拓展，产生一系列相关问题，通过对这些问题的探究，使学生反思原问题的本质，体验数学发现和创造的历程，有助于培养学生思维的深刻性.