TURBULENCE TRANSPORT OF SURFACTANT SOLUTION FLOW DURING DRAG REDUCTION DEGENERATION*

GU Wei-guo, WANG De-zhong

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: guweiguo@sjtu.edu.cn

(Received November 10, 2011, Revised February 13, 2012)

TURBULENCE TRANSPORT OF SURFACTANT SOLUTION FLOW DURING DRAG REDUCTION DEGENERATION*

GU Wei-guo, WANG De-zhong

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: guweiguo@sjtu.edu.cn

(Received November 10, 2011, Revised February 13, 2012)

Turbulence transport of surfactant solution flow during drag reduction degeneration is investigated experimentally in a two-dimensional channel. Particle Image Velocimetry (PIV) system is used to take two-dimensional velocity frames in the streamwise and wall-normal plane. The additive of surfactant is cetyltrimethyl ammonium chloride (CTAC) with the mass concentration of 25 ppm. Drag reduction degeneration happens in the CTAC solution flow, exhibiting the maximal drag reduction at =Re25 000 and losing drag reduction completely at =Re40 000. The velocity frames are statistically analyzed in four quadrants which are divided by the -uaxis and -νaxis. It is found that the phenomenon of “Zero Reynolds shear stress” is caused by the decrease of wallnormal fluctuations and its symmetrical distribution in quadrants. The increase of Reynolds number leads to the enhancement of turbulence burst phenomenon. During the drag reduction degeneration, the CTAC solution flow contains both high turbulence intensity and drag reduction states.

turbulence transport, surfactant, drag reduction degeneration, quadrant analysis

Introduction

The addition of polymer[1,2], surfactants[3,4]or fibers[5,6]into the turbulent water flow in ducts or pipes will lead to the decrease of friction. This phenomenon of drag reduction was firstly reported by Toms in 1948 and as a result, named as the Toms effect. Because it will reduce the pump power for water transporting, a lot of researchers studied the phenomenon even including the drag reduction in flexible tubes[7].

During the past decades, a lot of experiments and simulations have been carried out in order to clarify the mechanism of drag reduction. The early studies summarized the dynamic characteristics of drag-reducing flow, in which the transverse velocity fluctuations were strongly suppressed, whereas the streamwise component remained approximately the same level of water flow[8]. In the wall-bounded turbulent flow, the turbulence burst and Reynolds shear stressare important to clarify the turbulence transportation[9]. Li et al.[10-12]reported that the turbulence burst, turbulent structures and the inclination angle of the lowmomentum region were modified in the channel water flow if very little surfactant was added. The rheology of the surfactant solution, such as the viscoelsticity, was considered as one factor modifying the turbulence structures[13,14]. It is well known that surfactant additives added into the water will form the cross-linked micellar networks under a proper shear stress to damp the fluctuations, and the worm-like micelles were found by Cryo-TEM[15]. But the micelle is difficult to be investigated dynamically because of the shortage of present measuring method, so it is hard to explore directly the interaction between micelles and turbulent structures.

The Reynolds shear stress was strongly reduced in drag-reducing flow, accompanying with the decrease of turbulence transport. Kawaguchi et al.[16]ascribed the phenomenon to the less correlation between the two velocity fluctuations. But it does not explain how the turbulence transport is modified. Gu et al.[17]claimed that the “zero Reynolds shear stress”phenomenon was probably caused by the turnaroundtransportation happening in surfactant channel flow.

As is well known, drag reduction degeneration will appear in surfactant solution flow when the Reynolds number increases. The Reynolds shear stress will be changed step by step during the degeneration. This paper aims at studying the turbulence transport during the course in the very dilute surfactant solution channel flow. A Particle Image Velocimetry (PIV) system is used in the experiment. The fluctuations and Reynolds shear stress are analyzed in quadrants.

Fig.1 Schematic diagram of experimental facility

1. Experimental facilities

The experimental facilities and PIV system are shown in Fig.1. A closed-circuit water loop used in the experiment mainly contains a two-dimensional channel, water tank, an electromagnetic flow meter and one pump controlled by the frequency converters. The channel is made of transparent acrylic resin with the length (L) of 10 m, height (H) of 0.5 m and width (W) of 0.04 m. A honeycomb rectifier with a mean pore size of 0.15 m is set at the channel entrance for removing large eddies. The segment of PIV test lies 6 m downstream from the entrance of the channel. The electromagnetic flowmeter is installed upstream of the channel with uncertainty of ±0.01m3/min . Because the surrounding temperature is below 25oC, an electrical heater is installed in the waterotank for heating the circulating solution keeping at 25C with a measuring uncertainty of ±0.1oC.

The wall shear stress is estimated from the static pressure gradient which is tested between two pressure tabs located on the vertical side-wall of the channel with 1.5 m distance and the measuring uncertainty of 0.1Pa±.

The PIV system consists of a pair of Nd-YAG lasers, laser sheet optics, Charge-Coupled Device (CCD) camera, timing circuit, image-sampling computer and so on. The timing circuit communicates with the CCD camera and computer, and generates pulses to control the lasers. The CCD camera used in the experiment has a resolution of 2 048×2 048 pixels. Cartesian coordinates are also shown in the diagram that ,,xyz coordinates are determined by following streamwise, wall-normal, spanwise direction in the channel respectively. The laser sheet covers the streamwise and wall-normal (-xy) plane where =z 0.25m from the bottom of the channel. The tracers seeded in the flow are white waterbased synthetic resins coatings with a diameter of 0.1 μm-1 μm. When tracers are added into the solution, particle density is adjusted in order to give on average at least 10 particle pairs observed in an interrogation window.

The surfactant added to the water in this experiment is one kind of cationic surfactant, cetyltrimethyl ammonium chloride (CTAC). Sodium salicylate (NaSal) is added to the solution with the same mass concentration as CTAC for providing counterions. Because the experiment aims to examine drag reduction degeneration, the very dilute CTAC solution with the mass concentration of 25 ppm is selected.

Five different Reynolds numbers are selected in the experiments every 5 000 from 20 000 to 40 000. The Reynolds number is defined as Re=UbW/μ, wherebU is the bulk velocity of the channel flow, W is the width of the channel, and μ is the dynamic viscosity of the solution. However, the CTAC solution of 25 ppm is very dilute, so the dynamic viscosity of water is used in the calculation.

PIV frames are taken in water and 25 ppm CTAC solution flow respectively for comparison. Under every condition, five hundred of PIV image pairs are taken to generate two-dimensional vectors distributions. The frame covers the full width of the channel with the size of about x×y=5.8×10-2m×4.2× 10-2m. The interrogation area is set as 32×32 pixels with 75% overlap in each direction. As a result, the vector numbers are about 127×90 respectively in the x and y direction. The spacing between adjacent vectors is about 4.5×10-4m.

Fig.2 Frictional drag coefficients (fC) of 25 ppm CTAC solution, water flow and DR at Reynolds numbers between 20 000 and 40 000

Fig.3 Instantaneous distribution of streamwise velocity in -xy plane of 25 ppm surfactant solution and waterat Reynolds numbers between 20 000 and 40 000

2. Results and discussion

2.1 Friction factor and drag reduction

The Fanning friction factor (fC) and Drag Reduction (DR) are defined as

and

where τ is the wall shear stress,bU the bulk velocity, and ρ the density of water. The subscripts of“W” and “C” represent water and CTAC solution respectively.

In order to compare with the used equation, the following equations are Dean’s correlation of friction factor for a Newtonian fluid in a two-dimensional channel[18]and Virk’s ultimate correlation of friction factor for polymers solution flow[19].

Figure 2 exhibits that the friction of water obeys Dean’s equation well, and the friction of CTAC solution is markedly smaller than that of water, following the profile of Eq.(4) for Re smaller than 27 000. But as the Reynolds number is larger than 27000, the friction of CTAC solution increases quickly and reaches the friction level of the water at Re=40000. The maximum DR reaches nearly 80% in 25 ppm CTAC solution at Re=25000.

According to the division of DR state, the Reynolds number at which DR reaches the maximum is called the first critical Reynolds number and the Reynolds number at which DR disappears completely is called the second critical Reynolds number. Between the two critical Reynolds numbers, DR decreases gradually and disappears at last, and this phenomenon is called drag reduction degeneration. In this experiment, the highest DR state lies in the Reynolds numbers of 20 000 and 25 000, while DR degeneration lies in the Reynolds numbers of 30 000 and 35 000. DR disappears at Re=40000.

2.2 Instantaneous distribution of streamwise νelocity

Figure 3 shows the two-dimensional instantaneous contour of streamwise velocity (/UUτ) , where Uτis the friction velocity. The flow of water is shown in Fig.3(a) and the flow of CTAC solution fluids are shown in Figs.3(b) to 3(f) with the Reynolds number decreases from 40 000 to 20 000. When the Reynolds numbers are at 25 000 and 20 000 as shown in Figs.3(e) and 3(f), the CTAC solution is in the state of the highest drag reduction. The contours exhibit the approximately parallel layered pattern, whereas the contours are contorted in water flow as shown in Fig.3(a). When the Reynolds number increases, the distributed pattern of CTAC solution fluids gradually become similar to the water flow. The change of the instantaneous distributions indicates that the velocity fields of drag reducing flow become turbulent and irregular during drag reduction degeneration.

At the same time, there are a lot of small altitude circles in the central region of the channel, especially appearing in the drag reducing flow such as in Figs.3(d) to 3(f). These small altitude circles reflect the velocity fluctuations with small geometric dimensions. It is indicated that the decrease of shear rate will weaken the ability to suppress the fluctuations and the local flow exhibits slight turbulence.

2.3 Mean νelocity, rms and Reynolds shear stress

At the same Reynolds number, five hundred of velocity frames are used to carry out statistical calculation. The vectors for ensemble average along the streamwise direction are about fifty thousand at one identical y coordinate. Figure 4 presents the profiles of mean streamwise velocity handled dimensionlessly with friction velocity (uτ) which is marked by the superscript “+”.

The log law equation of mean velocity for Newtonian turbulent flow and the ultimate velocity profile of polymeric solution flow suggested by Virk are shown as Eqs.(5) and (6).

where y+is defined as y+=yρuτ/μ.

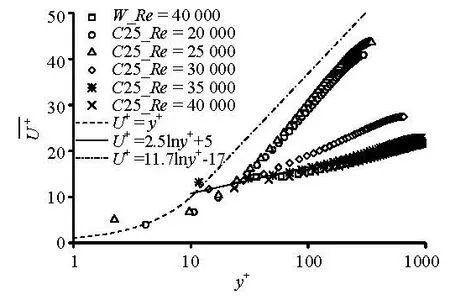
Fig.4 U+distributed profiles of 25 ppm surfactant solution and water at Reynolds numbers between 20 000 and 40 000

In Fig.4, the mean streamwise velocity of water is distributed in close agreement with the profile given by Eq.(5). The profiles of 25 ppm CTAC solution at Re=40 000 and 35 000 are also distributed near the profile of the water because drag reduction disappears at these Reynolds numbers. At the same time, the profiles of 25 ppm CTAC solution at Re=20 000 and 25 000 are distributed upwards and close to that given by Eq.(6) because the fluids are at the highest drag reduction state.

The profiles of Reynolds shear stress across half width of the channel are shown in Fig.5. The abscissa in the figure is the wall-normal coordinate (y*) in the channel where the superscript “*” represents the dimensionless geometry by the half width of channel (y*=2y/W ). As is well known, the sum of Reynolds shear stress and viscous shear stress obeys the equation of τ=1-y*, and the Reynolds shear stress dominates over the flow out of the boundary layer. As is shown in Fig.5, the profile of water flow agrees with the law, but the Reynolds shear stress of CTAC solu-tion decreases quickly with the increases of Reynolds number and surprisingly approaches zero at =Re 25 000 and 20 000. The phenomenon of Reynolds shear stress staying near zero across the whole channel in drag reducing flow is called the zero Reynolds shear stress.

Fig.5 Distributed profiles of Reynolds shear tress across half width of the channel in 25 ppm surfactant solution and water at Reynolds numbers between 20 000 and 40 000

Fig.6 rms distributed profiles of velocity fluctuations across half width of the channel in 25 ppm surfactant solution and water at Reynolds numbers between 20 000 and 40 000

The root mean square (rms) defined in Eq.(7) is used to analyze turbulence intensity where N represents the number of the vectors in calculation.

Figure 6 exhibits the rms-distributed profiles of streamwise velocity fluctuations (+u) and wall-normal velocity fluctuations (+ν) respectively. As is shown in Fig.6(a), the rms of streamwise component is distributed larger than the water when 25 ppm CTAC solution flow lies in high drag reduction state. In contrast, the rms of the wall-normal component of drag reducing flow is remarkably smaller than the water, especially reaches the minimum at =Re25 000 and 20 000. This is the so-called phenomenon that transverse velocity fluctuations are suppressed.

However, greater-than-zero rms implies that the fluctuations are not diminished completely and the fluid is not the laminar flow. So the appearance of“zero Reynolds shear stress” phenomenon does not indicate there is no turbulence transport in drag reducing flow.

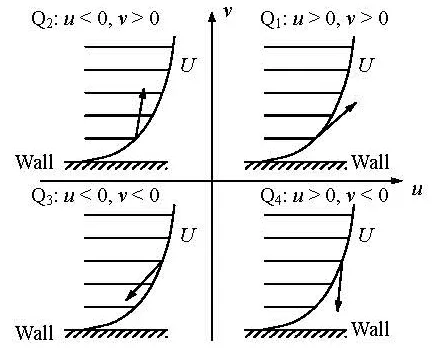
Fig.7 Schematic diagram of the categorization of turbulent fluid motions in quadrants

2.4 Analysis in quadrants

Figure 7 is the schematic diagram of fluid motions categorization in quadrants according to the plus or minus of two velocity fluctuations. In the first quadrant, the streamwise velocity fluctuation is plus, implying the local velocity larger than the mean velocity, and the wall-normal component is also plus, implying the fluid moving away from the wall. According to this analogy, the streamwise component is plus in the first and forth quadrant, minus in the second and third quadrant. At the same time, the wall-normal component is plus in the first and second quadrant, minus in the third and forth quadrant.

When the turbulence burst happens, the fluid jumps from the wall to the bulk flow and mixes with the local high speed fluid (0ν＞), then the mixed streamwise velocity is lower than the mean streamwise velocity (0u＜), which will lie in the second quadrant. At the same time, when the accompanying sweep motion happens, the high speed fluid sweeps toward the wall (0ν＜) and the streamwise velocity ishigher than the local velocity (0u＞), which will lie in the forth quadrant. The above-mentioned course indicates that the turbulence transport when turbulence burst happens usually is categorized into the second quadrant and forth quadrant.

Fig.8 Distributed profiles of Reynolds shear tress across half width of the channel in 25 ppm surfactant solution and water at Reynolds numbers between 20 000 and 40 000 in quadrants

If the cross-correlation of the two fluctuations is calculated by using the fluctuations in one quadrant as defined in Eq.(8), the statistic result will represent the contribution in the Reynolds shear stress of No. i quadrant.

As is shown in Fig.8(a), the water flow exhibits that the main contributors are the second and forth quadrant, especially the second quadrant has the largest value of cross-correlation across the whole width of the channel. At the same time, the crosscorrelation is steady at the small value in the first and third quadrants.

Figures 8(e) and 8(f) show the different distribution characteristics of cross-correlation in 25 ppm CTAC solution flow with the highest drag reduction state. The profiles of cross-correlation in the second and forth quadrants decrease and become almost symmetrical to the profiles in the first and third quadrants. Consequently, the symmetrical distribution with the u-axis leads to the sum of the cross-correlation in all quadrants decreasing to zero. It is indicated that the“zero Reynolds shear stress” phenomenon is caused by the decrease of cross-correlation in the second and forth quadrants and the symmetrical distribution with the u-axis.

Fig.9 rms distributed profiles of streamwise velocity fluctuations across half width of the channel in 25 ppm surfactant solution and water at Reynolds numbers between 20 000 and 40 000 in quadrants

Fig.10 rms distributed profiles of wall-normal velocity fluctuations across half width of the channel in 25 ppm surfactant solution and water at Reynolds numbers between 20 000 and 40 000 in quadrants

With the Reynolds number increasing, the crosscorrelation in the second and forth quadrants increases accordingly as shown in Figs.8(d) to 8(b). The increase firstly appears in the fluid near the wall and gradually reaches the level of the water flow. As is shown in Fig.8(d) at Re=30000, the cross-correlation becomes large only where y*＜0.5.

Similarly, the rms is also categorized into the quadrants as defined by the following equation

Figures 9 and 10 show the rms distribution of streamwise and wall-normal velocity fluctuations in quadrants. In Figs.9(b) and 9(d), the profiles in second and forth quadrants are similar in both water flow and CTAC solution flow except at Re=30000. But in the first and third quadrants, the RMS of 25 ppm CTAC solution at =Re20 000 and 25 000 is larger than that in water and another CTAC solution flow with drag reduction degeneration. It is proved that the rms of streamwise velocity fluctuations is enhanced when drag reduction appears. But this increase mainly appears in first and third quadrants. At the same time, the wall-normal component in the first and third quadrants, the rms of CTAC solution flow is a little smaller than that in water. But it decreases quickly in the second and forth quadrants versus the drag reduction level. So the decrease of wall-normal velocity fluctuations mainly appears in the second and forth quadrants.

2.5 Discussion

The instantaneous streamwise velocity frames, rms, and appearance of “zero Reynolds shear stress”indicate that the fluctuations in the transverse direction are suppressed in the CTAC solution flow when high drag reduction appears. But the phenomenon of“zero Reynolds shear stress” is not caused by the laminar flow state but by the symmetrical distribution of fluctuations in quadrants. Compared with the water flow, drag reducing flow exhibits the distribution of fluctuations with small inclined angle with the u-axis. The wall-normal fluctuations are minimized, and streamwise fluctuations are enhanced. However, the decrease of the wall-normal fluctuations mainly focuses on the second and forth quadrants, while it is almost not changed in the first and third quadrants. Because the second and forth quadrants are dependent on the turbulence burst and sweep motion, these results indicate that the turbulence transport is reduced in drag reducing flow.

During drag reduction degeneration of 25 ppm CTAC solution flow when the Reynolds number increases, the vectors with high wall-normal fluctuation grow in number gradually in the second and forth quadrants, and this phenomenon indicates turbulence burst events being strengthened. However, the rise of wall-normal fluctuations firstly happens in the flow only near the wall, and small fluctuations are still maintained in the bulk flow such as in the CTAC solution flow at Re=30000. This phenomenon implies that the increase of Reynolds number strengthens the turbulence burst to break the suppression in drag reducing flow, which will firstly start from the wall. But the turbulence transport will be diminished quickly if the Reynolds number is not large enough, and at this time the part fluids further away from the wall will remain the state of drag reduction. It will lead to the solution containing both high turbulence and drag reduction states during the drag reduction degeneration. The characteristics are usually ignored in simulation.

3. Conclusions

Two-dimensional velocity fields of the channel flow have been examined by PIV measurements in the experiments aimed at studying water and 25 ppm CTAC solution at the Reynolds number from 20 000 to 40 000. The experimental data are statistically analyzed in quadrants which are divided by the u-axis and ν-axis. The following conclusions are drawn from the study.

(1) Drag reduction degeneration happens in 25 ppm CTAC solution which exhibits the maximal drag reduction at Re=25000 and lose drag reduction completely at Re=40000.

(2) The phenomenon of “zero Reynolds shear stress” appearing in drag reduction flow is caused by the symmetrical distribution of fluctuations in quadrants. The minimization of wall-normal fluctuations and Reynolds shear stress indicates that the turbulence burst and the accompanying sweep motion is supperssed.

(3) The increase of Reynolds number in CTAC solution flow leads to the increase in the number of high wall-normal fluctuations in the second quadrant and forth quadrant. In the course of drag reduction degeneration, turbulence transport is enhanced, but the solution will contain both turbulence and drag reduction states.

Acknowledgement

The experiments were carried out in Kawaguchi’s laboratory at Tokyo University of Science, Japan.

References

[1] KIM N.-J., KIM S. and LIM S. H. Measurement of drag reduction in polymer added turbulent flow[J]. International Communications in Heat and Mass Transfer, 2009, 36(10): 1014-1019.

[2] SHAO X., LIN J. and Wu T. et al. Experimental research on drag reduction by polymer additives in a turbulent pipe flow[J]. Canadian Journal of Chemical Engineering, 2002, 80(2): 293-298.

[3] KAWAGUCHI Y., SEGAWA T. and Feng Z. et al. Experimental study on drag-reducing channel flow with surfactant additives-spatial structure of turbulence investigated by PIV system[J]. International Journal of Heat and Fluid Flow, 2002, 23(5): 700-709.

[4] MYSKA J., MIK V. Application of a drag reducing surfactant in the heating circuit[J]. Energy and Buildings, 2003, 35(8): 813-819.

[5] LIN J. Z., GAO Z. Y. and ZHOU K. et al. Mathematical modeling of turbulent fiber suspension and successive iteration solution in the channel flow[J]. Applied Mathematical Modelling, 2006, 30(9): 1010-1020.

[6] YOU Zhen-jiang, LIN Jian-zhong and SHAO Xue-ming et al. Stability and drag reduction in transient channel flow of fibre suspensions[J]. Chinese Journal of Chemical Engineering, 2004, 12(3): 319-323(in Chinese).

[7] CAI Shu-peng. Influence of Young’s modulus on dragreduction in turbulent flow using flexible tubes[J]. Journal of Hydrodynamics, 2010, 22(5): 657-661.

[8] GYR A., TSINOBER A. On the rheological nature of drag reduction phenomena[J]. Journal of Non-Newtonian Fluid Mechanics, 1997, 73(1): 153-162.

[9] FUKAGATA K., IWAMOTO K. and KASAGI N. Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows[J]. Physics of Fluids, 2002, 14(11): L73-L76.

[10] LI F.-C., KAWAGUCHI Y. and SEGAWA T. et al. Reynolds-number dependence of turbulence structures in a drag-reducing surfactant solution channel flow investigated by particle image velocimetry[J]. Physics of Fluids, 2001, 17(7): 075104.

[11] LI F.-C., KAWAGUCHI Y. and HISHIDA K. et al. Investigation of turbulence structures in a drag-reduced turbulent channel flow with surfactant additive by stereoscopic particle image velocimetry[J]. Experiments in Fluids, 2006, 40(2): 218-230.

[12] LI F.-C., KAWAGUCHI Y. and YU B. et al. Experimental study for drag-reduction mechanism for a dilute surfactant solution flow[J]. International Journal of Heat and Mass transfer, 2008, 51(3-4): 835-843.

[13] GU W., KAWAGUCHI Y. and WANG D. et al. Experimental study of turbulence transport in a dilute surfactant solution flow investigated by PIV[J]. Journal of Fluids Engineering, 2010, 132(5): 1-7.

[14] ZHANG Hong-xia, WANG De-zhong and GU Wei-guo et al. Effects of temperature and concentration on rheological characteristics of surfactant additive solutions[J]. Journal of Hydrodynamics, 2008, 20(5): 603-610.

[15] GONZÁLEZ Y. I., KALER E. W. Cryo-TEM studies of worm-like micellar solutions[J]. Current Opinion in Colloid and Interface Science, 2005, 10(5-6): 256-260.

[16] KAWAGUCHI Y., TAWARAYA Y. and YABE A. et al. Turbulent transport mechanism in drag reducing flow with surfactant additive investigated by two component LDV[C]. Eighth International Symposium Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 1996, 29.4.1-29.4.7.

[17] GU W., WANG D. and KAWAGUCHI Y. Analysis of zero Reynolds shear stress appearing in dilute surfactant drag-reducing flow[J]. Advances in Mechanical Engineering, 2011, 367042.

[18] DEAN R. B. Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct[J]. Journal of Fluids Engineering, 1978, 100(2): 215-223.

[19] VIRK P. S., MICKLEY E. W. and SMITH K. A. The ultimate asymptote and mean flow structure in Tom’s phenomenon [J]. Journal of Applied Mechanics, 1970, 37(2): 488-493.

10.1016/S1001-6058(11)60269-2

* Project supported by the National Natural Science Foundation of China (Grant No. 51106095) the China Postdoctoral Science Foundation (Grant No. 20110490717).

Biography: GU Wei-guo (1979-), Male, Ph. D.