MODELING DAM-BREAK FLOOD OVER NATURAL RIVERS USING DISCONTINUOUS GALERKIN METHOD*

LAI Wencong, KHAN Abdul A.

Glenn Department of Civil Engineering, Clemson University, Clemson, S.C., USA, E-mail: wlai@clemson.edu

(Received October 12, 2011, Revised January 15, 2012)

MODELING DAM-BREAK FLOOD OVER NATURAL RIVERS USING DISCONTINUOUS GALERKIN METHOD*

LAI Wencong, KHAN Abdul A.

Glenn Department of Civil Engineering, Clemson University, Clemson, S.C., USA, E-mail: wlai@clemson.edu

(Received October 12, 2011, Revised January 15, 2012)

A well-balanced numerical model is presented for two-dimensional, depth-averaged, shallow water flows based on the Discontinuous Galerkin (DG) method. The model is applied to simulate dam-break flood in natural rivers with wet/dry bed and complex topography. To eliminate numerical imbalance, the pressure force and bed slope terms are combined in the shallow water flow equations. For partially wet/dry elements, a treatment of the source term that preserves the well-balanced property is presented. A treatment for modeling flow over initially dry bed is presented. Numerical results show that the time step used is related to the dry bed criterion. The intercell numerical flux in the DG method is computed by the Harten-Lax-van Contact (HLLC) approximate Riemann solver. A two-dimensional slope limiting procedure is employed to prevent spurious oscillation. The robustness and accuracy of the model are demonstrated through several test cases, including dam-break flow in a channel with three bumps, laboratory dam-break tests over a triangular bump and an L-shape bend, dam-break flood in the Paute River, and the Malpasset dam-break case. Numerical results show that the model is robust and accurate to simulate dam-break flood over natural rivers with complex geometry and wet/dry beds.

Discontinuous Galerkin (DG) method, shallow water flows, dam-break flood, well-balanced scheme

Introduction

Dam-break flood can cause significant environmental damage and loss of property and human life. Understanding flow characteristics such as maximum water level and flood arrival time is fundamental to engineering design and safety. Numerical modeling and understanding of flows in natural rivers have been a great challenge to hydraulic engineers and researchers. Simulation of natural free surface flows is a complex task due to complicated bottom geometry, irregular boundaries, and dry bed condition. The twodimensional, depth averaged, shallow water equations, named the Saint-Venant equations, have been widely used to model the shallow water flows in natural rivers, lakes, estuaries, and coastal zones. The twodimensional flow simulation models can provide adequate information to describe the flows and flooding properties such as depth, velocity, flood extent, and wave arrival time.

As the Finite Volume Method (FVM) can be used to deal with flow discontinuities and complex geometry, a number of numerical methods based onthe FVM have been developed to solve the shallow water equations on unstructured grids[1-3]. Recently, the Runge-Kutta Discontinuous Galerkin (RKDG) Finite-Element Method (FEM) has gained great popularity in solving hyperbolic conservative equations such as shallow water equations[4,5]. The Discontinuous Galerkin (DG) method is a combination of FVM and FEM. So the DG method preserves advantages of both FVM and FEM, such as shock capturing, higher spatial accuracy, and resolving complex geometries.

The DG method was first introduced to solve the neutron transport equation. The RKDG method was further developed for the solution of non-linear, timedependent, hyperbolic equations. In recent years, significant progress has been achieved in DG method applications, such as dam-break flow, coastal wave disturbance and tidal flows[6,7], flooding and drying[8,9]. However, the application of DG method in dam-break flow in natural rivers is missing. Schwanenberg and Harms[5]modeled the Malpasset dam-break flow without providing detailed results.

To preserve the still water or well-balanced property in the scheme, modified shallow water equations[10-12], flux modification[8,9]and surface gradient method[13]can be used. In the present work, the sha-llow water equations used by Ying et al.[10]are adopted, and a simple treatment of well-balanced property in the DG method is given. In the DG method, the numerical flux is crucial to its accuracy. Several approximate Riemann solvers can be used to obtain the first-order upwind numerical flux, like the Roe flux, Harten-Lax-van Leer (HLL), Harten-Lax-van Contact (HLLC), and weighted average flux. The HLLC flux, which can model equations with three characteristic eigenvalues[14], is used for the two-dimensional shallow water equations in the present study. Treatment of flooding and drying is also provided. A two-dimensional slope limiting procedure for linear triangular element is given. The rest of the paper is organized as follows. The shallow water equations and DG method are first briefly described. Then, the numerical flux and the slope limiter procedure are provided. Later, several test cases are treated to validate this scheme. Last, summary and brief conclusions are given.

1. Governing equations

The two-dimensional shallow water flow equations are applicable in situations where the horizontal extent is much greater than the depth of flow and vertical acceleration may be neglected[15,16]. The twodimensional shallow water equations are derived by integrating the Navier-Stokes equations in the vertical direction under the assumption of uniform velocity profile in the vertical direction and hydrostatic pressure distribution. The vector form of the depth-averaged, two-dimensional, shallow water flow equations can be written as

where the vectors of conserved variables, fluxes in the x and y directions, and the source term can be written, respectively, as follows: where h is the water depth,Z is the water surface level, qx=hu and qy=hv are the unit width flow rates in thex and y directions, respectively,u and v are the velocity components in thex andy directions, respectively,g is the gravitational acceleration, and n is Manning’s roughness coefficient.

Fig.1 Discretization using triangular elements in DG method

2. Formulation of DG method

A typical mesh configuration for linear triangular elements in the DG method is shown in Fig.1. The main element (0) and the three surrounding elements (1, 2 and 3), as shown in the figure, have independent vertices. A group of vertices form a node. The number of vertices at a node depends on the number of elements joining the node. For vector F with componentsE and G, corresponding to the x and y components, respectively, Eq.(1) can be written in its vector form as

Within an element, the variation of variables is approximated by the values of the variables at the vertices and shape functions (=NjUj,j=1,2,3), where Njis a diagonal matrix of basis function and Ujis a column vector of the variable given in Eq.(2). Equation (3) is multiplied by the weight function, which is the same as basis function for the Galerkin method, and the resulting equation is integrated over an element. The discontinuous Galerkin formulation, where the flux term is integrated by parts, results in the following equationwheren represents the numerical flux across the boundaries of an element and n is the outward unit normal vector at the element boundary. The discontinuous elements are connected through the numerical flux across a common boundary. Thus, the accuracy with which the numerical flux is calculated is crucial to the DG method.

3. Numerical flux

The numerical flux across a boundary of an element in Eq.(4) can be evaluated using a variety of upwind numerical flux functions. The use of discontinuous elements in the discontinuous Galerkin method ensures that a generalized local Riemann problem can be solved for the numerical flux. In this study, the HLLC flux function is adopted[6].

For the rotation matrix and its inverse given in Eq.(5), the rotational invariance of the flux results in Eq.(6). By defining V=TU, the numerical flux, obtained using the inverse of the rotational matrix and numerical flux, is given by Eq.(7)

Fig.2 Structure of a three-wave HLLC solver

The HLLC flux is based on the assumption of a three-wave system as illustrated in Fig.2, which is the case for two-dimensional shallow water equations. The numerical flux, computed from HLLC flux function is given by Eq.(8).

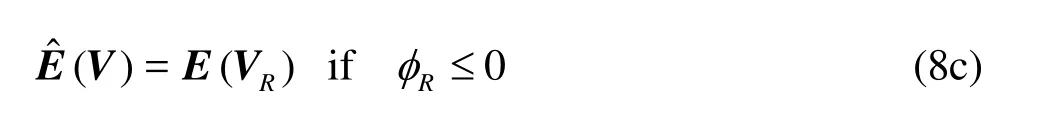
In the above equation, the subscripts L and R stand for the left- and right-hand sides of the element boundary, respectively. If the velocity components in the direction normal and tangential to the element boundary are denoted as unand ut, respectively, then the wave speeds and rotated conserved variables in the star region can be estimated as:

For dry bed problems, the numerical flux is evaluated through a two-wave HLL flux function given by

where EL=E(VL), ER=E(VR) and the wave speed for right dry bed and left dry bed are, respectively, given by:For problems with initially dry bed, water depth and velocity of zero are used as initial conditions, and a tolerance depth ε is used to check wet/dry front[17]. If water depth is greater than ε on one side of an element face and is smaller than ε on the other side, then numerical flux is calculated by Eqs.(15) according to the dry bed element location and wave speeds are calculated with either Eq.(16) or Eq.(17). If water depth on both sides is smaller than ε, then numerical fluxand source term S are set to zero. After a time step, if the computed water depth at a node is smaller thanε, then the depth and velocity at that node are set to zero.

4. Source term treatment

The calculation of the water level slope in the source term can be determined using Green’s theorem as follows[10]:

where Z0jis the water level at the boundary of element 0 and the surrounding element j(j=1,2,3), which can be determined by water surface of these two elements by weighted factors such as distance, and Ω0is the area of element 0. Numerical results show that this treatment of source term can accurately discretize the pressure force term.

The well-balanced property in wet domain is satisfied with Eq.(1). The still water with partial wet domain can be easily achieved by setting the source term S to be zero in both partial wet elements and dry elements. In addition, the slope limiter is not applied in elements with zero velocities. Although the source term in partial wet elements is forced to be zero, numerical tests in dam-break flows show that the flood waves are still accurately modeled.

5. Slope limiting procedure

A slope limiting procedure modified from Tu and Aliabadi[18]is used for incompressible flows in this study. Tu and Aliabadi[18]applied the slope limiter on the primitive variables in compressible flows. In this study, the slope limiter is applied on the conserved variables for incompressible flows in order to conserve mass and momentum. So this procedure would be one step less. A concise and consistent way to calculate the element gradient is used here. The limiting procedure includes the following steps.

The average solution of the conserved variable is calculated at the element centroid. Arithmetic mean of solutions at nodes of an element is taken as the average solution and given by Eq.(20). Using the interpolation functions and vertex solutions, Eq.(21) is used to find the unlimited gradient in each element.

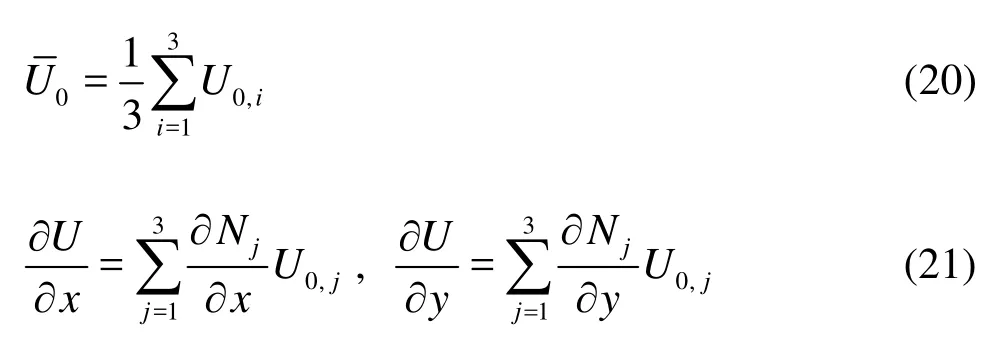
The limited gradient in an element is computed by taking the weighted average of the unlimited gradient in the surrounding elements as given below

where the weigh factors are given by

where δ is a small number introduced to prevent indeterminacy and the gradient terms, which are the square of the L2norm of the unlimited element gradients, are given by

Finally, the limited conservative variables at vertices of each element are computed. The requirement for the reconstructed solution,, is to satisfy each component of limited gradient and preserve the average at the element centroid as given by

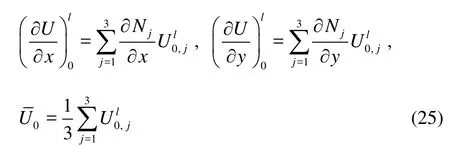
6. Time integration

The Total Variation Diminishing (TVD) Runge-Kutta time integration scheme is used in this paper. The TVD Runge-Kutta time integration and the slope limiter are adopted here to eliminate numerically generated oscillations near shocks and steep gradients and to achieve the TVD property. To conserve the TVD property, the Runge-Kutta time integration scheme should be one order higher than the shape functions. The second-order two-stage TVD Runge-Kutta scheme is employed for the linear shape function used. The resulting scheme would be of second-order accuracy in space and time. Equation (4) can be written in the following form

To advance the solution from time step n to n+1, the second-order TVD Runge-Kutta scheme can be written as

Numerical tests for flow with dry bed show that the time step is also dependent on the dry bed depth criterion adopted. As the dry bed depth criterion is reduced, the wave speed will increase, so the time step should be reduced to satisfy the Courant-Friedrichs-Lewy (CFL) condition. So a reduction in the dry bed depth requires a decrease in time step to achieve stable results. A smaller dry bed depth will provide more accurate results at the cost of smaller time step, hence higher computational expense.

7. Numerical results

7.1 Test 1: Stationarity test over bumps

The well-balanced property of the scheme is tested by simulating initial still water over a channel with three bumps and constant water surface level. The channel is 75 m long and 30 m wide with closed wall, and channel bottom is defined by

The water surface elevation is initially 0.5 m in the whole channel, covering partially the bumps. The domain is triangulated with 5 006 elements. A time step of 0.01 s is used. Computed water surface at 100 s is shown in Fig.3, indicating that the stationarity state is well preserved.

Fig.3 Water surface at 100 s for stationarity test with bumps

Fig.4 Initial conditions of dam-break flow over three bumps

7.2 Test 2: Dam-break flow over bumps

The channel in test 1 is used in this test with different initial conditions as shown in Fig.4. The dam is located at 16 m and retains water to the depth of 1.875 m upstream, while the bed is dry downstream of the dam. Manning’s roughness coefficient is 0.018 s/m1/3. The dam is assumed to be removed instantaneously, and the dam-break flow afterward is simulated. The dry bed depth criterion (ε) of 0.001 m and time step of 0.01 s are used. Numerical tests show that decrease in dry bed depth criterion requires decrease in time step to achieve stable results.

Numerical results of water surface at different times, 2 s, 6 s, 12 s, 30 s and 300 s after the removal of the dam, are presented through Figs.5-9 to show the flood propagation and wetting and drying capability ofthe numerical scheme. At time of 2 s, the flood wave reaches the two smaller bumps and begins to run up. At time of 6 s, flood wave overtops the two smaller bumps and the water accumulates behind the highest bump. A reflective bore is moving upstream. At time of 12 s, the floodwater passes the highest bump and begins to flood the lee side. The drying of the highest bump and the reflective bore moving further upstream is clear. At time of 30 s, wave interaction between the bump and the downstream wall is shown. The steady state water surface at 300 s shows the peaks of the smaller bumps are no longer submerged. The flooding and drying effect on this complicated bed topography is properly simulated with this numerical scheme.

Fig.5 Water surface at 2 s for dam-break flow with bumps

Fig.6 Water surface at 6 s for dam-break flow with bumps

Fig.7 Water surface at 12 s for dam-break flow with bumps

Fig.8 Water surface at 30 s for dam-break flow with bumps

Fig.9 Water surface at 300 s for dam-break flow with bumps

Fig.10 Geometry and experimental set up in the channel with triangular bump

7.3 Test 3: Dam-break flow over a triangular bump

In this test, the numerical scheme is used to model dam-break flow over a triangular bump as proposed by the Concerted Action on Dam-break Modeling (CADAM) project. Numerical results are compared with experimental data obtained from Laboratoire de Recherches Hydrauliques, Châtelet (Belgium). The rectangular channel is 38 m long, 0.75 m wide with a gate located at 15.5 m from upstream end. The symmetric triangular bump (6 m long, 0.4 m high) is situated at 13 m downstream of the gate. The initial condition and bed bottom are shown in Fig.10. Water depth upstream the gate is 0.75 m with dry bed downstream. Manning’s roughness coefficients are 0.0125 and 0.011, respectively, for bed and the walls as suggested by Hiver. Free outflow boundary condition is applied at the outflow end. The computational domain is triangulated with 4 352 elements. The dry bed depth of 0.001 m and time step of 0.006 sare used. Simulated and measured hydrograph at 90 s after the dam removal at gauge points G2, G4, G8, G10, G11, G13 and G20 are shown in Figs.11-17. Gauge points denote distance from the gate, for example, G2 is located 2 m downstream of the gate. The simulated results are in good agreement with the measured data. The flood wave arrival time and water depth are well predicted at all gauge points. The wetting and drying effect at the critical point G13, which is located at the vertex of the bump, is modeled correctly. Difference between simulated and measured results at the final point G20 mostly comes from the uncertainty of the actual outflow boundary condition. Maximum water depth predicted at G8, G10 and G11 are higher than experimental measurements. This may be due to the turbulence effect, air entrainment, or roughness difference at the bump transition.

Fig.11 Simulated and measured hydrograph at gauge G2

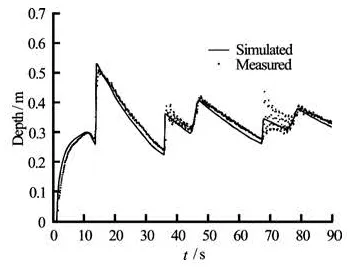
Fig.12 Simulated and measured hydrograph at gauge G4

Fig.13 Simulated and measured hydrograph at gauge G8

Fig.14 Simulated and measured hydrograph at gauge G10

Fig.15 Simulated and measured hydrograph at gauge G11

Fig.16 Simulated and measured hydrograph at gauge G13

Fig.17 Simulated and measured hydrograph at gauge G20

7.4 Test 4: Dam-break in a channel with 90obend

Physical models were built in the Civil Engineering Department Laboratory, Université Catholique de Louvain (UCL, Belgium) to model dam break and strong transient flows in sharp bends. Experimental data were collected and used to validate the numerical models by the CADAM group.

Fig.18 Plan view of channel with 90obend

The shape of the horizontal channel with 90obend is shown in Fig.18. The dam is represented by a gate at the outlet of the reservoir. The initial water level in the upstream reservoir is 0.2 m above the horizontal channel bed, and the channel downstream is dry. Manning’s roughness coefficients of 0.0095 s/m1/3for bottom friction and 0.0195 s/m1/3for wall friction are adopted as suggested. The computational domain is triangulated with 8 546 elements. The dry bed depth of 0.0001 m and time step of 0.002 s are used.

Fig.19 Simulated and measured hydrograph at G1

Fig.20 Simulated and measured hydrograph at G2

Fig.21 Simulated and measured hydrograph at G3

Fig.22 Simulated and measured hydrograph at G4

Fig.23 Simulated and measured hydrograph at G5

Fig.24 Simulated and measured hydrograph at G6

After the removal of the gate, water flows rapidly into the channel and reaches the bend. The water re-flects against the wall and a shock forms and moves upstream. The simulated hydrographs at six gauging points are compared with measured data in Figs.19-24. Numerical results are in good agreement with the measured data. The arrival time of the flood wave and reflected bore are well predicted except at G2, where the simulated bore arrival time is too early. This may be due to the assumption of an instantaneous removal of the gate, while in fact the removal takes time. Also, strong turbulent flows occur at the entrance and after the bend with possible air entrainment, so the numerical results at G2 and G5 are not in good agreement with measured data. Overall, the simulated results give satisfactory performance.

Fig.25 Initial water depth contour for Paute River test (m)

7.5 Test 5: Paute river dam-break event

In this test, the numerical scheme is used to model a dam-break flood in the Paute River, Ecuador. In 1993, a landslide created a natural dam, which blocked the flow and created a reservoir upstream of the Paute River. Due to high water level in the reservoir, the dam was subsequently overtopped and caused a dam-break type flood. River topography and triangulation data are available from BreZo. The dam-break case is used to test the ability of presented numerical scheme to handle flow in natural rivers with complex geometry and sharp bends, though field data are not available. A case with measured data will be given in next test. The computational mesh with 74 224 elements and initial water depth are shown in Fig.25. The dam is considered as a straight line between (x, y) coordinates of (739 602 m, 9 684 690 m) and (739 616 m, 9 684 530 m), and separates upstream and downstream region. The initial upstream water level is 2 362 m above sea level and downstream is dry. The bed elevations range from 2 155.2 m to 2 917.8 m above sea level. Manning’s roughness coefficient is set to be 0.033 in the domain. The dam is assumed to be removed completely and instantaneously. The dambreak flood afterward is simulated. The dry bed depth criterion of 0.04 m and time step size of 0.01 s are used. The computed water depth contour (flood inundation map) at 10 min, 20 min, and 40 min after the dam-break are presented in Figs.26-28. The numerical results are similar to the results reported by Song et al.[3]. The dam-break floods follow the river channel (area with dense mesh). The flood wave travels about 6 000 m in the first 10 min, then encounters a sharp bend and travels about 6 000 m during 20 min-40 min. Numerical results show that the scheme is able to model flow in natural rivers with wet/dry bed conditions and sharp bends.

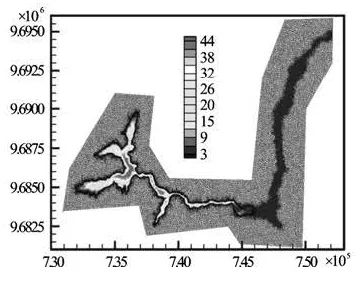
Fig.26 Computed water depth contour for Paute River dambreak test att=10min

Fig.27 Computed water depth contour for Paute River dambreak test att=20min

Fig.28 Computed water depth contour for Paute River dambreak test att=40min

7.6 Test 6: Malpasset dam-break event

The Malpasset dam was located in a narrow gorge of the Reyran River Valley in France. The damwas 66.5 m high with variable thickness and the upper crest had an elevation of 223 m, and formed a reservoir with capacity of 5.5×107m3. In 1959, the dam failed due to intense rainfall and rapid increase of water level in the reservoir. The maximum water levels along the Reyran River Valley after the dam failure were obtained from a police survey (these points are denoted P1-P17). In 1964, a physical model with a scale of 1:400 was built by Laboratoire National d’Hydraulique to study the dam-break flow. The maximum water level and flood wave arrival time were recorded at 9 points in the physical model and these points are denoted as S6-S14.

Fig.29 Mesh and locations of surveyed points and gauges

Due to the availability of the measured data and complex bottom topography, the Malpasset dam-break event was adopted as a benchmark test for CADAM projects. This event is simulated to validate the numerical model. The computational domain with 26 000 elements and measured points are shown in Fig.29. The domain covers an area approximate of 17 500 m× 9 000 m. The bed elevations range from –20 m below sea level to 100 m above sea level. The Reyran River has two sharp narrow bends immediately downstream of the dam and eventually reaches the coastal floodplain.

The dam is considered as a straight line between (,)xy coordinates of (4 701.18 m, 4 143.41 m) and (4 656.5 m, 4 392.1 m). The initial water level inside the reservoir is set to 100 m above sea level, and the computational domain downstream of the dam is considered as dry bed. The initial discharge in the Reyran River before dam failure is neglected because of the relatively huge amount of flow caused by the dam failure. The model is simulated until the water reaches the sea, so no boundary condition is applied at the downstream end. Manning’s roughness coefficient is estimated to be in the range of 0.025 s/m1/3-0.033 s/m1/3, equivalent to a Strickler coefficient in the range of 30 s/m1/3-40 m1/3/s as was suggested by Electricité De France (EDF). The dry bed depth of 0.02 m and time step size of 0.01 s are used. The computed and measured flood front arrival time at gauges (S6-S14) are shown in Fig.30.

Fig.30 Simulated and measured wave front arrival time

Fig.31 Simulated and measured maximum levels at gauges

Fig.32 Comparison of computed and measured maximum water level at surveyed points

The computed and measured maximum water level at gauges and surveyed points (P1-P17) are presented in Figs.31 and 32, respectively. The effect of Manning’s roughness coefficient is investigated, a uniform value of 0.025 and 0.033 in the whole computational domain are compared with the measured data. Lower roughness (0.025, solid line) corresponds to a faster moving front (Fig.30) and lower water levels (Figs.31-32). A roughness coefficient of 0.029 gives the best estimation. The difference between different roughness coefficients in maximum water level is small. The computed results for both flood arrival time and maximum water levels are generally in good agreement with the field data.

Fig.33 Computed water depth contour for Malpasset dam-break test at t=800s (m)

Fig.34 Computed water depth contour for Malpasset dam-break test at t =1800s (m)

Fig.35 Computed water depth contour for Malpasset dam-break test at t =2400s (m)

The water depth contour (flood inundation map) at 800 s, 1 800 s, and 2 400 s with roughness coefficient of 0.029 are presented in Figs.33-35. The flood wave propagation and inundation area are well modeled with high mountains at downstream floodplain. The results show that the present scheme is capable of dealing with dam-break flows over wet/dry bed with complex topography.

8. Conclusion

A well-balanced numerical model has been developed for two-dimensional, depth-averaged, shallow water flows based on discontinuous Galerkin method. The model is applied to simulate dam-break flood over natural rivers with complex topography and wet/ dry beds. In the shallow water equations, the pressure force term and the bed slope term are combined to eliminate numerical imbalance. The well-balanced property is achieved by forcing the source term to be zero in partially wet elements and dry elements. A simple treatment for flow over dry bed and for checking wet/ dry front is presented. Numerical results show that the time step used is related to the dry bed depth criterion. The intercell numerical flux is computed by the HLLC approximate Riemann solver. A two-dimensional limiting procedure is employed to prevent spurious oscillation. The performance of the model is tested through several test cases, including dam-break flow in a channel with three bumps, laboratory dam-break tests over a triangular bump and an L-shape bend, dam-break flood in the Paute River, and the Malpasset dam-break case. Numerical results demonstrated that the model is robust and accurate to simulate dambreak flood in natural rivers with complex geometry and wet/dry beds. It will be interesting and important to include the effect of turbulence in shock wave modeling in future work.

[2] PAN Cun-hong, DAI Shi-qiang and CHEN Shen-mei. Numerical simulation for 2D shallow water equations by using Godunov-type scheme with unstructured mesh[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(4): 475-480.

[3] SONG L., ZHOU J. and LI Q. et al. An unstructured finite volume model for dam-break floods with wet/dry fronts over complex topography[J]. International Journal for Numerical Methods in Fluids, 2010, 67(8): 960-980.

[4] FAGHERAZZI S., RASETARINERA P. and HUSSAINI M. Y. et al. Numerical solution of the dam-break problem with a discontinuous Galerkin method[J]. Journal of Hydraulic Engineering, ASCE, 2004, 130(6): 1-8.

[5] SCHWANENBERG D., HARMS M. Discontinuous Galerkin finite-element method for transcritical twodimensional shallow water flows[J]. Journal of Hydraulic Engineering, ASCE, 2004, 130(5): 412-421.

[6] ESKILSSON C., SHERWIN S. J. A triangular spectral/ hp discontinuous Galerkin method for modeling 2D shallow water equations[J]. International Journal for Numerical Methods in Fluids, 2010, 45(6): 605-623.

[7] AIZINGER V., DAWSON C. A discontinuous Galerkin method for two-dimensional flow and transport in shallow water[J]. Advances in Water Resources, 2002, 25(1): 67-84.

[8] ERN A., PIPERNO S. and DJADEL K. A well-balanced Runge-Kutta discontinuous Galerkin method for the shallow-water equations with flooding and drying[J]. International Journal for Numerical Methods in Fluids, 2008, 58(1): 1-25.

[9] XING Y., ZHANG X. and SHU C. Positivity-preserving high order well-balanced discontinuous Galerkin

[1] YOON T. H., KANG S. Finite volume model for twodimensional shallow water flows on unstructured grids[J]. Journal of Hydraulic Engineering, ASCE, 2004, 130(7): 678-688.methods for the shallow water equations[J]. Advances in Water Resources, 2010, 33(12): 1476-1493.

[10] YING X., JORGESON J. and WANG S. S. Y. Modeling dam-break flows using finite volume method on unstructured grid[J]. Engineering Application of Computational Fluid Mechanics, 2009, 3(2): 184-194.

[11] KESSERWANI G., LIANG Q. A discontinuous Galerkin algorithm for the two-dimensional shallow water equations[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(49-52): 3356-3368.

[12] SONG L., ZHOU J. and GUO J. et al. A robust wellbalanced finite volume model for shallow water flows with wetting and drying over irregular terrain[J]. Advances in Water Resources, 2011, 34(7): 915-932.

[13] LIANG Qiuhua. A coupled morphodynamic model for applications involving wetting and drying[J]. Journal of Hydrodynamics, 2011, 23(3): 273-281.

[14] GUO Yan, LIU Ru-xun and, DUAN Ya-li et al. A characteristic-based finite volume method scheme for shallow water equations[J]. Journal of Hydrodynamics, 2009, 21(4): 531-540.

[15] LI H., LIU R. The discontinuous Galerkin finite element method for the 2D shallow water equations[J]. Mathematics and Computers in Simulation, 2001, 56(3): 223-233.

[16] LAI Y. G. Two-dimensional depth-averaged flow modeling with an unstructured hybrid mesh[J]. Journal of Hydraulic Engineering, ASCE, 2010, 136(1): 12-23.

[17] SANDERS B. F. High-resolution and non-oscillatory solution of the St. Venant equations in non-rectangular and non-prismatic channels[J]. Journal of Hydraulic Research, 2001, 39(3): 321-330.

[18] TU S., ALIABADI S. A slope limiting procedure in discontinuous Galerkin finite element method for gasdynamics applications[J]. International Journal of Numerical Analysis and Modeling, 2005, 2(2): 163-178.

10.1016/S1001-6058(11)60268-0

* Biography: LAI Wencong (1985-), Male, Ph. D.