工程设计的偏微分方程描述系统非线性的数学与工程基础简要

2012-08-22程襄武

科学之友 2012年18期

程襄武

（南京化工职业技术学院机械系，江苏南京 210048）

1 工程设计的系统分析与偏微分方程

工程设计的核心是设计计算。现代工程设计将对象抽象为工程系统，在数学上更抽象为动力系统，分析其动态进行设计计算。所谓动力系统是在系统内在规律反复作用下按时间变化发展的系统。[2，3]传统计算方法采用集总的静态方法，在典型工况附近达到较高效率，但实际系统运行是在整个过程即全工况下进行，因此达不到整体过程最优。采用全过程工况基础上的过程设计方法[6]笔者认为更为合理，可以得到更符合实际的系统特性作为计算基础。

系统过程的数学模拟是上述计算为基础。动态模拟主要有机理建模与辨识建模等方法。由于实际过程的复杂性，机理建模时不可行，辨识建模日益重要，可处理很多非线性问题。现代科学计算的智能算法多属辨识建模的非线性算法，尽管有许多基于不确定性的，依据统计规律的方法，传统机理建模依然是重要手段，与系统关系更密切，可反映系统内部关系与过程。其模型与动力系统的定义一致，是物理、化学等自然规律、机制作用的数学表现形式，具体形式为描述系统的偏微分方程。集总参数或分布参数系统的分析形式都可采用，更细致全面的分布参数系统一般是偏微分方程形式。设计计算关键即成为偏微分方程的求解问题，这些偏微分方程常常以非线性形式出现。

2 微分方程概念、类型及一般形式

2.1 微分方程定义及分类大概

微分方程是表示未知函数、未知函数的导数与自变量之间的关系的方程；若未知函数是一元函数即常微分方程（OED），若未知函数是多元函数即偏微分方程（PDE）。[4，5]涉及一个或几个未知函数及其导数的偏微分方程组成一个偏微分方程方程组；偏微分方程（组）的阶数是其导数最高阶数[7]。常微分与偏微分的类型划分是依据未知函数与自变量的数量对应。微分方程的阶亦可作为微分方程分类依据。以方程系数来分，可分常系数方程与变系数方程。按非线性性质来分，微分方程可分为线性、非线性及拟线性方程。按非线性性质的方程分类不仅仅是数学形式，更和过程与规律的实质有深刻的联系。

2.2 常微分方程与偏微分方程形式

工程问题的微分方程由物理、化学，乃至机械、电控等复杂规律、机理确定，形式多样，繁简不一。在理论上，其微分方程属应用数学领域，以下简略概括其数学形式。

2.2.1 常微分方程形式例举

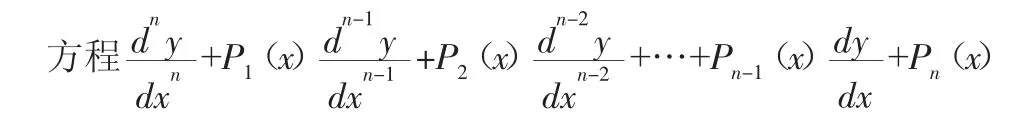
y=R（x）（方程①）是 n 阶常微分方程，若 R（x）=0，则称齐次方程[8]。

显然是一个自变量x，及一个因变量y（x）的情形。

2.3 线性与非线性微分方程形式例举

2.4 偏微分方程一般形式写法

3 微分方程与动力系统的形式关系与实质关系

偏微分方程与动力系统简称为方程与系统。方程是系统的描述，系统以方程形式表现。方程较系统更抽象，更表现实质。系统形式以方程形式确定，方程形式即是系统形式。同样方程表现出的实质是系统的实质，但不是全部。这可由方程建立的阶段特点与模型的近似性来理解。一般我们总是先确定系统，以系统基础才可确定方程，最后通过方程了解系统更深层次实质，但近似性决定这种实质不是全部。

系统直接以方程表述其许多形式或特性。例如，动力系统若是单输入单输出系统，其描述方程是常微分方程；若是多输入多输出系统，其描述方程是偏微分方程。前述方程①描述单输入单输出系统，方程②～⑦描述多输入多输出系统。上述方程（组）⑦若看作工程系统的偏微分方程描述，显然是n个x输入，m个u输出的动态系统，并可看成工程系统偏微分方程的普遍形式。以微分方程的形式可对系统定性分析，以确定工程问题的正确方案。又如，若方程是线性的则系统称为线性系统；系统方程是非线性的则系统称非线性系统[1]，方程的形式确定系统的特性。

4 方程与系统的线性与非线性

非线性与线性是方程与系统都具有的特性。方程的线性与非线性的形式特征决定系统的线性与非线性的形式，并确定其性质特征。系统的线性与非线性性质可表现为物理实在。

由于学生成长的环境不同，受教育情况不同，有些学生思想政治意识欠佳，没有树立正确的世界观、人生观和价值观，以致于遇到问题时，容易偏激，不能理性分析问题、解决问题，这在一定程度上增加了高校辅导员管理工作的难度。要想使学生拥有健全的思想政治意识，高校辅导员必须注重加强对学生的思想教育工作，使他们树立正确的世界观、人生观和价值观，养成良好的处事习惯。

4.1 偏微分方程的线性与非线性

4.1.1 线性与非线性的定义

若偏微分方程（组）关于所有未知函数及其导数都是线性的，则称线性偏微分方程（组），否则成为非线性偏微分方程（组）。非线性偏微分方程（组）若对未知函数的最高阶导数是线性的，则称拟线性偏微分方程（组）。[11]我们可将偏微分方程看成关于未知函数以及未知函数对各自变量的偏导函数的方程，并注意方程相对于此两类函数的系数项的特点对线性与非线性的形式成因，以及线性与非线性是方程的形式特征。

4.1.2 线性与非线性的判定

线性与非线性由偏微分方程的组成项的特点决定其定义，并可由组成项的形式特征判定。即若微分方程的每一项最多只含有因变量或因变量的各阶导数的一次方幂，不包括因变量或其各阶导数的高次方幂，也不包含这些函数的乘积，则称这个方程是非线性的。[1]注意此处虽是古典控制论的单输入单输出的常微分方程情形，[1，12]但可推到多输入多输出的一般情形，与前述定义根本一致。线性微分方程所有应变量及其导数的系数可是常数，也可是一个或几个自变量的函数。[8]应注意线性与非线性非此即彼，一个偏微分方程不是线性的，就称为非线性的。[10]

4.1.3 线性与非线性偏微分方程的解

非线性偏微分方程的解析解极为困难，可与线性及常微分方程的求解相比较得知。与常微分方程比较，求解复杂性体现在常微分方程的解一般依赖于若干常数，偏微分方程的解自由度往往更大，可能很多，一般很难用通解形式表示，即对线性方程也如此。往往更多研究偏微分方程在初始与边界等定解条件下的解。虽然许多常见偏微分方程不考虑定解条件，解的自由度很大，但许多偏微分方程却连一个解也不存在，这种现象奇特。偏微分方程与常微分方程的不同形成两个不同数学分支。[11]

与线性方程比较，求解复杂性体现在叠加原理对非线性方程不再成立，求解更困难。拟线性方程非线性程度较弱，比一般的非线性方程容易些。[11]线性方程可利用解的叠加性原理求解。无论常微分或偏微分方程的线性齐次微分方程都具叠加性质，即若z1、z2都是线性齐次偏微分方程的特殊解，那么c1z1+c2z2，其中c1，c2是常量，也是方程的一个解。并且若zn都是特殊解，收敛级数∑cnzn也是方程的一个解，只要此级数可以任意微分。[8]一定条件下可根据已知解序列构造级数形式的解，或根据已知含参数的解来构造积分形式的解。[11]

4.1.4 工程问题的偏微分方程近似解

4.1.4.1 偏微分方程的解的适定性

工程问题要得到偏微分方程的适定定解。偏微分方程的定解问题就是满足适当初始或边界条件等附加条件的解的问题。若定解问题满足至少一个解的存在性，只有一个解的唯一性，解连续依赖于给定已知数据的稳定性，则称为是适定的。不能简单认为物理问题有解则定解问题也有解；物理问题可以有唯一解但定解问题的解可多于一个；稳定性是必须的要求，对描述特定物理现象的定解问题，给定的数据的微小变化最多只能产生解的微小变化。[10]定解问题存在唯一解，且定解条件的原始资料作微小变化时，解也仅作微小变化，这时我们称该定解问题是稳定的。合理的定解问题应当满足解的存在、唯一和稳定三个要求，存在性、唯一性和稳定性统称为定解问题的适定性。[11]显然，适定性的要求较为严格，此特点决定了偏微分方程的求解难度。

4.1.4.2 偏微分方程的工程近似解

由于非线性的影响，适定解析解极其困难。常系数线性方程组求解比较简单，可导出解析解。[15]变系数的线性系统或非线性微分方程只能用级数解法，或仅能用定性方法研讨解的性质，仅对具备某些特点的方程才可用变换技巧求解。[14]绝大多数变系数、非线性、不规则几何等复杂问题，数学的解析方法几乎无能为力。[13]

因此，工程技术中的定解问题，往往无法求得其准确解，可借助近似解法，常用的有差分法、变分法、有限元法。[16]解决非线性微分方程的求解和研究它所描述的复杂现象和过程的时间演化和动态行为，只能依靠计算机和实验方法。按照理论的设计来进行各种数值运算与模拟，方便地改变控制参数以改变动态结果，并可在时间与空间的大、中、小诸尺度上进行模拟研究。[13]工程实际系统的非线性影响的复杂性，甚至使得数值近似计算亦极困难，例如，相对于线性最优控制易求得解析解，许多非线性最优控制问题不能用计算机求解，即使有解，计算工作也繁重。[19]工程设计必须定量计算。工程系统涉及的偏微分方程，现代工程设计的定量计算对于非线性问题主要以其数值解为基础，或采用线性近似进行计算。

4.2 系统的线性与非线性

工程系统的定量，方程是手段与基础，系统是过程与目的。工程设计要对工程系统定量才能完成以交付制造并运行，设计计算是定性分析基础上的定量分析。系统线性非线性特征分析属定性分析，是其工作前阶段。系统的动态特性与描述系统的微分方程的类型密切相关，微分方程的类型可确定对提出的系统合理问题的性质，即对系统进行定性分析，方程类型可确定工程问题的正确解法。[1]

4.2.1 线性与非线性系统的划分

描述系统的偏微分方程是线性的系统称线性系统，若系统的描述方程是非线性的称非线性系统。[1]显然，方程的形式决定系统的形式，系统的形式根据方程的形式划分。此外，线性系统分常系数线性系统与变系数线性系统两类。若描述方程的每一项的系数都是常数，则称常系数线性系统；不是常数而是自变量的函数，则称变系数线性系统。[1]

4.2.2 线性系统特点概要

线性系统的动力学行为均可由一组一阶线性方程组表示，这组微分方程的解，结合初始条件与边界条件，可以精确地反映该系统的动力学过程。[20]若系统输入为u1=[u11，u21]T，u2=[u12，u22]T，输出为y1=[y11，y11]T，y2=[y12，y12]T，则若系统输入为u=u1+u2时，系统的输出为y=y1+y2，则称系统有加性。若系统输入u放大K倍时，输出y也放大K倍，则称系统有齐性。系统对输入和初始条件都满足加性和齐性，则称其满足叠加原理。满足叠加原理是线性系统的基本特征，表征线性系统的线性方程组也满足叠加原理。[15]线性系统的研究在数学上包括线性微分方程、傅立叶分析、线性算子理论和随机过程的线性理论在内的强有力的解析方法和工具。[13]显然，工程系统采用线性近似以线性系统处理易于定量。线性系统满足叠加原理，整体等于部分之和。[13]体现在实际系统的物理实在特点上，例如，一台电炉加热可获一份热量，两台则可获两份；由牛顿第二定律，一定质量物体受一定力作用得到一定加速度，力增加一定倍数则加速度增加相同倍数。[20]但是，在实际过程里，线性系统只是理想的或近似的，它是真实系统在特定状态附近线性化的结果。[20]

4.2.3 非线性系统特点概要

非线性系统主要特点是复杂性。工程设计的系统复杂性体现在非线性的不稳定、不确定、难以求解。工程系统的数学抽象目的在于定量计算，非线性系统的处理成为难点。例如，常系数线性系统的稳定性分析较为简单，进展到变系数线性系统变得较复杂，非线性系统即使极简单的非线性方程的动态已出现较高复杂性，稳定与不稳定性可同时出现，一般提出的稳定性问题已无意义。[1]但实际过程多是非线性的，非线性现象在自然界广泛存在，线性只是平衡态附近的近似。[20]工程过程的描述偏微分方程常是非线性的。传统上线性近似计算即可，现代工程设计计算更多采用计算机方法进行更符合工程实际的优化设计，面临更多非线性系统的处理。

5 工程设计的工程系统的非线性问题及处理

工程设计的计算理论显然应基于确定论，其工程系统的动态分析应该是确定的、可预测的。工程设计的专业系统千差万别，但数学抽象的理论方法大致相同，面临的非线性问题是共同的，不稳定、难解和复杂性是共同特点，精准高效的现代设计要求直接面对非线性的实际过程。工程系统若可近似作常系数线性系统则易求解，实际的变系数的线性系统或非线性微分方程，只能有级数解法或数值积分解法求解，工程设计计算以此大都即可完成。但有时仅能定性讨论涉及方程解的性质，一些形式非常简单的偏微分方程，初始条件的微小误差会引起解的很大改变，即使可确定解的存在唯一，甚至用某些方法已得到这个解，仍然很难说这个解能真实反映过程实际。[11]即有时即使是工程数值解，也存在解的可靠性问题。甚至“某些实际系统的偏微分方程模型可以产生混沌，[14]导致系统特性无法预测。工程设计可以利用非线性导致的混沌现象进行混沌控制[18]，根据需要增强或抑制混沌，例如，利用混沌增强换热。[17]控制混沌的方法，都是通过对实际过程的偏微分方程的理论分析及数值计算找到的。[17，18]

工程设计无论以何种方式完成设计计算，认知与判定工程系统与其偏微分方程的形式与非线性特点，并进行设计定性分析以及设计定量是必要的。

[1]钱学森.工程控制论[M].北京:科学出版社，1958:1-4.

[2]Jurgen Jost.Dynamical Systems-Examples of Complex Behaviour[M].Springer-Verlag Berlin Heidelberg，2005:1.

[3]高普云.非线性动力学：分叉、混沌与孤立子[M].北京:国防科技大学出版社，2005.

[4]同济大学数学教研室.高等数学(下册)[M].北京:高等教育出版社，1996:322.

[5]Alan Jeffrey.Advanced Engineering Mathematics[M].HARCOURT/ACADEMIC PRESS.

[6]陈在康，丁力行.空调过程设计与建筑节能[M].北京:中国电力出版社，2004:44-45.

[7]F·约翰.偏微分方程[M].北京:科学出版社，1986:1.

[8]H.Betz，P.B.Borcham，G.M.Bwing.微分方程及其应用[M].上海：上海科学技术出版社，1958.

[9]刘适式，刘适达.物理学中的非线性方程[M].北京:北京大学出版社，2000.

[10]Tyn.Myint-U.数学物理中的偏微分方程[M].上海：上海科学技术出版社，1983.

[11]陈恕行.偏微分方程概论[M].北京:人民教育出版社，1981.