基于三角级数法的U型槽底板内力计算
2012-08-22李宁
李 宁
(中铁二院工程集团有限责任公司 四川 成都 610031)
0 引言
随着我国经济建设推进,铁路及公路等交通基础设施建设也得到了迅猛发展。U型槽作为一种适用于地下水丰富、地下水位较高、放坡条件受到限制的挖方路基地段的新型结构,同时具有节约土地资源、环境影响小的特点,因此在近几年的高速铁路建设[1]、城市交通建设中被广泛应用。
作为一种新型结构,业内针对该结构的计算方法尚不够成熟,而其他大型通用计算软件在计算U型槽结构时,要求设计人员具备足够的经验,设置合理的计算边界条件,因而使计算过程变得十分复杂。因此研究U型槽结构的理论计算方法具有重大的实际意义。
在计算中,边墙计算按悬臂挡墙计算,其土压力按主动土压力考虑。底板受到边墙所传递的内力,以及其他边界荷载的共同作用,其受力条件复杂。底板计算一般采用经验类比法估算底板内力,或者按弹性地基梁法加以计算。文本结合铁路工程实例,充分考虑计算方法对铁路实际工程适用性,采用三角级数法对U型槽底板内力进行计算。
1 三角级数法[2]
1.1 基本公式
考虑图2所示等截面梁。梁的长度为2l,宽度为b,设ξ=x/l,抗弯刚度为EI,地基模量为E0。梁上受任意分布荷载q(ξ),有:

图2 模型简图

设地基反力为p(ξ),则梁的平衡条件方程是:

1.2 配点方程
根据弹性理论中弗拉芒公式,在半无限体表面作用一集中力P,距力作用点r处的一点相对于另一点D(距力作用点d)的沉陷是:

因此,对于压力p(ρ)作用范围内的任意一点ξ,由ρ处微段荷载p(ρ)ldp引起的沉陷在荷载作用范围内积分,就可以得到:

引入沉陷函数U(ξ),整理得到

1.3 地基反力表达式
将地基反力展开为余弦级数:

将式(6)代入平衡条件方程(式(2)),可得

地基反力确定后,梁的内力可以下式计算:
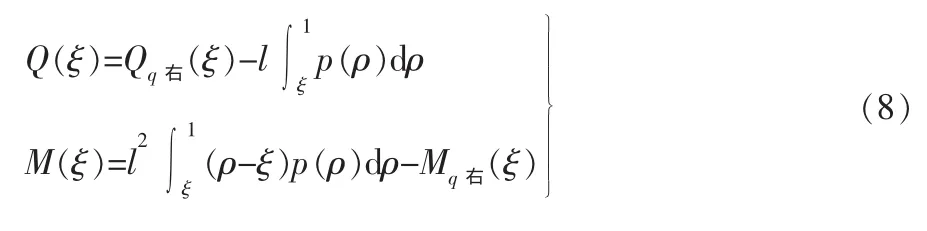
式中:Qq右(ξ)、Qq右(ξ)为脱离体上的外荷载简化到 ξ截面处的合力及力矩。
2 工程实例
某线新建时速200km/h客运无砟轨道铁路U型槽,工程参数如下
(1)结构尺寸:底板宽 16.4m,高 1.0m,边墙高 H=6m,厚度0.8m;
(2)设计水位:运营阶段地下水位为地表以下1.0m;
(3)墙背回填卵石土参数:容重 γ=21kN/m3,浮容重 γ`=11kN/m3,内摩擦角 φ=35°,粘聚力 c=0kPa;
(4)地基土弹性模量:E=200MPa;
(5)材料:U型槽底板、边墙均采用C35混凝土;
(6)计算单元:沿线路方向取1m单位宽度作为计算单元。
按库伦土压力计算边墙主动土压力,整理底板荷载如图3所示,底板自重荷载 qG=25kN/m3,边墙自重qb=150kN/m3,趾板配重qp=126kN/m3,换算土柱荷载qL=65kN/m3,边墙传递弯矩M=330kN·m。采用三角级数对底板内力进行计算,并与郭氏查表法及文克尔模型法计算结果进行对比分析。

图3 底板计算荷载示意图(尺寸单位:m)
(1)地基反力沿底板横向分布如图4所示,三角级数法计算所得地基反力最大值138.12kN/m,出现在底板两侧端部,中部地基反力量值逐渐缩小,最小值71.37kN/m,出现在底板中部;郭氏查表法计算所得地基反力分布规律与三角级数法基本相同,最大值151.22kN/m出现在底板两侧端部;文克尔模型法计算所得地基反力量值沿底板横向变化较小,最大值99.48kN/m;

图4 地基反力图
(2)底板剪力横向分布如图5所示,三角级数法计算所得底板剪力最大值111.072kN,出现在边墙与底板衔接处,中部及趾板两侧剪力逐渐减小;郭氏查表法计算所得底板剪力分布规律与三角级数法基本相同,最大值103.93kN;文克尔模型法计算所得底板剪分布规律与前两种方法基本相同,但量值略大,底板剪力最大值133.11kN;
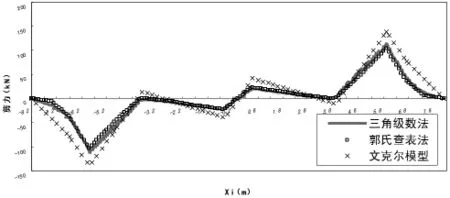
图5 底板剪力图
(3)底板弯矩横向分布如图6所示,三角级数法计算所得底板正弯矩最大值312.34kN·m,出现在边墙与底板衔接处内侧,边墙与底板衔接处外侧出现部分负弯矩,量值达到-13.65kN·m;郭氏查表法计算所得底板剪力分布规律与三角级数法基本相同,正弯矩最大值313.27kN·m,负弯矩最大值-16.73kN·m;文克尔模型法计算所得底板正弯矩最大值260.61kN·m,出现在在边墙与底板衔接处右侧,边墙与底板衔接处左侧出现部分负弯矩,量值达到-57.99kN·m,底板两侧边墙衔接处内侧正弯矩逐渐减小,在中部位置出现部分负弯矩,量值为-13.42kN·m。
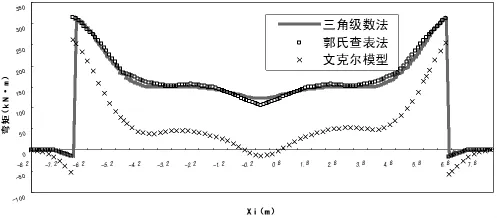
图6 底板弯矩图
3 结语
3.1 三角级数法更好的放映了地基的连续性,更复合实际情况的地基反力。
3.2 用三角级数法计算U型槽底板内力的力学模型明确,参数较少,计算步骤简洁,适合于工程计算和程序开发使用。
[1]杨维加.弹性地基梁的三角级数解法[M].北京:中国水利水电出版社,2005:19-75.
[2]李海光.新型支挡结构设计与工程实例[M].2版北京:人民交通出版社,2011:431-452.
[3]崔满.三角级数法模拟弹性地基梁内力[J].山西建筑,2007,7(19):96-97.
[4]赵冬娇.封闭式路堑U型槽结构的研究[D].吉林大学,2010.
