BP神经网络在信号发生器中的应用

徐明哲

（中国电子科技集团公司第四十一研究所 山东 青岛 266555）

0 引言

模拟信号源中关键部件压控振荡器的输出频率与调谐电压之间是非线性关系，通常都是使用线性关系来简单的表示两者之间的关系，只要知道某两个频点的调谐电压，根据两点一线原理，就可以确定该线性关系，根据此线性关系，其它频率点的调谐电压就可以通过该线性关系找出，事实上，振荡器输出频率与控制电压并非严格的遵循线性关系，而是非线性的，如图1所示：

图1 输出频率与调谐电压关系图

从图中可以直观的看出，在振荡器输出频率的低端和高端非线性很明显，因此若根据线性函数得到的调谐电压v0加到振荡器上，并不一定会输出目标频率f0，而是fn，并且，f0与fn之间的差值可能非常大，使控制振荡器的锁相环路从fn锁定输出到f0的时间非常长，从而影响了仪器的性能，鉴于此，本文提出了一种基于BP神经网络的方法来拟合压控振荡器输出频率与控制电压关系的函数fbp（v），使得f0与fn更接近以致相等，将此关系取代线性关系应用到振荡器的调谐电压设置上将会缩短控制环路的锁相时间，提高仪器性能。

1 模拟合成信号源简介

信号发生器的信号产生方式主要有两种：模拟合成和直接数字合成。模拟合成信号源主要是依靠最核心的压控振荡器振荡器来产生信号，并通过外围控制电路来满足信号的指标要求，如为满足信号的功率指标，可以加功率电平控制电路，为满足信号的频率调制指标，可以以反馈环路的方式加频率控制电路，如用小数环外加其它环路来控制频率精度，为降低噪声加本振环路等，最终的目的就是得到精准的调谐电压来控制振荡器，使之锁定在要求输出的频率的工作状态[1]，模拟信号源工作原理如图2所示。

图2 模拟合成信号源原理示意图

如图所示，当预置电压很准确的时候，输出频率将会很快锁定。模拟信号源认为，YIG振荡器的输出频率与加在YIG振荡器上的电压成线性关系，该线性关系如公式（1）所示。

其中f（v）是调谐电压为 时的输出频率；

a为斜率；

b为截距；

根据两点一线原理， 只要有两个样点A （v1，f（v1））,B（v2，f（v2））就可以确定该公式的 a 和 b，如下所示：

根据经验，两个样点一般选取振荡器频率输出范围的三分之一和三分之二处，当要输出目标频率fm时，根据公式1，可以得出求控制电压vm的公式

所以，模拟合成源一般只校准两个频点的预置电压值，根据公式2就可以确定整个频率范围的预置电压。

事实上，振荡器输出频率和控制电压之间并非严格的遵循线性关系，因此，当使用公式（2）来确定某特定输出频率fm的控制电压vm时，给振荡器施加预置电压vm，振荡器实际输出频率为fr，此时fm≠fr，并且误差频率能非常大，这给锁相环路将振荡器振荡频率从fr锁定到fm增加了耗时，当误差频率超过锁相环路的捕捉带宽时，会导致锁相环失锁，因此寻找一种合适的算法来准确描述输出频率和调谐电压之间的关系是有必要的，鉴于BP神经网络有很强的非线性映射能力，同时原理简单易于实现，本文提出一种使用BP神经网络模型来描述频率和调谐电压之间关系的方法。

2 BP神经网络模型的建立

2.1 BP神经网络

BP神经网络属于前馈型网络，具有很强的非线性映射能力，通常由输入层、输出层和若干个隐层构成[2]，结构如图3所示。

图3 BP神经网络结构图

神经网络的基本组成单元为神经元，同一层神经元中没有任何耦合，每一节点的输出只影响下一层节点的输出。网络的学习过程由正向和反向传播两部分组成。第k层第i个神经元的结构如图4所示。

图4 神经元结构图

f（·）为作用函数，一般取硬限幅函数或Sigmoid函数，本文中拟采用Sigmoid函数，其定义如下：

其中，Xj=ΣWijXi

2.2 BP神经网络学习算法

对于给定的总层数为P的BP神经网络，其学习样本集为（（Xl，Dl），l＝1，2，…，S，网络学习的目的为求各层的权系数Wij（k），k＝1，2，…，P，使全局误差 E 达到最小值。 其中 n 为输出神经元个数。

在开始训练时，网络的全部权值必须初始化，一般设置为较小的随机数，这可保证不因权值取最大值而使网络出现饱和或出现反常情况。

BP算法的训练步骤如下：

1）从样本集中取一样本对，把输入矢量用作网络的输入；

2）计算网络输出矢量；

3）计算网络输出矢量与样本对的目标矢量的差；

4）再从输出层反向计算到第一中间层，向减少差错方向调整网络权值；

5）对样本集中每一个样本对重复上述1至4步，直到整个样本集的差错最小。

学习结束是指实际输出矢量与目标矢量间差错已减少到可接受的值，权值已不再调整。

权值的调整根据Delta规则进行。

Wij（n＋1）＝Wij（n）＋ηδjX′j

其中，Wij（n）为神经元i至神经元j的第n次变更的权值，X′j为神经元i的输出，η为学习率常数，δj为神经元j的差值。如何向减少差错方向调整权值是关键，BP算法一般是采用梯度下降原理，即在权值空间中沿梯度方向搜索。有关BP算法的更详细知识可参考文献[3]。

3 实验结果与讨论分析

在本实验中，输入矢量和输出矢量均为1维，中间层数和每一层神经元个数选的太少，不利于网络的学习，选的太多，虽然会提高模拟精度，但是会影响工作效率，因此，综合考虑，采取折衷，兼顾效率和精度。每层神经元的个数选取10个，中间层选取4层，权值调整算法采用梯度下降算法。本文中使用的信号发生器压控振荡器振荡器输出频率范围是5GHz～10GHz，调谐电压范围是 0～20v，训练输入样本集采用在整个频率范围内随机抽取100个样点，开发环境为VC2005，首先使用样本集中的样点训练神经网络，通过迭代的方法计算出各个神经元之间的权值，然后将神经网络应用到信号发生器中，设置要输出的频率，神经网络将会计算出压控振荡器对应该频率的电压值，将该值送到设置振荡器调谐电压的寄存器，振荡器将会起作用输出设置频率，各个频点的设置结果如图5所示。

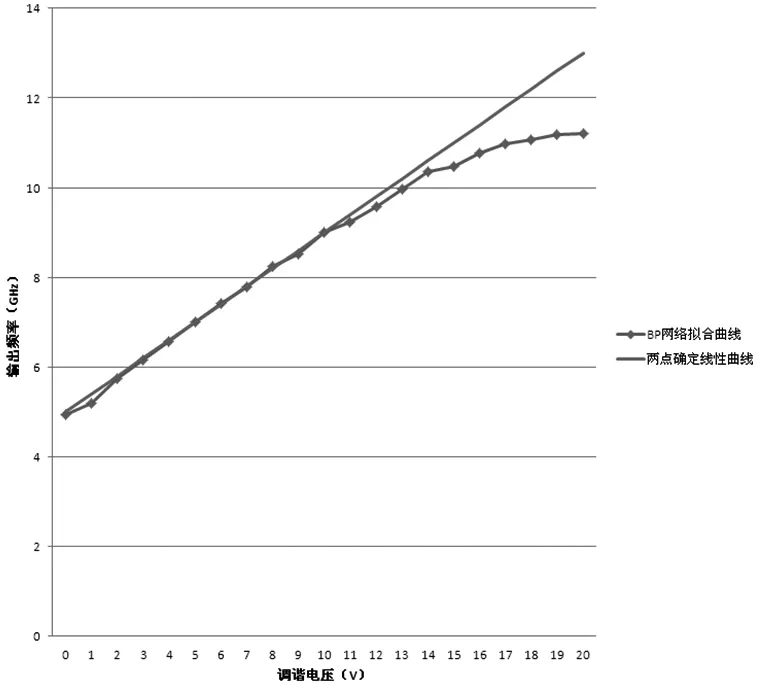
图5 BP网络拟合曲线与线性曲线对比图

与图1对比可以看出采用BP神经网络虽然不能完全逼近图1中的曲线，但是相对于直线已经有很大改观。

4 小结

通过构造简单的BP神经网络来拟合振荡器输出频率与调谐电压之间的关系，摆脱了振荡器输出高端和低端的非线性，在点频模式下能够准确的输出预置频率，缩短了锁相环路的工作时间，提高了工作效率。但是在扫频时由于磁滞现象的存在，扫速的不同会导致不同的非线性曲线，该问题有待于从理论和应用方面进一步认识和研究。

［1］信息产业部电子41研究所.现代通信测量仪器[M].北京：军事科学出版社,1999：39-52.

［2］王伟.人工神经网络原理：入门与应用[M].北京：北京航空航天大学出版社,1995：100-105.

［3］杨行峻,郑君里.人工神经网络[M].北京：高等教育出版社,1991：70-76.