阿司匹林合成体系三组分的拉曼光谱测定及应用*

孙阔，粟晖，姚志湘，黄培贤，苏传婷

(广西工学院生物与化学工程系，广西柳州 545006)

阿司匹林作为一种光谱的解热镇痛的非甾体抗炎药是由水杨酸乙酰化反应制得，传统的分析方法为滴定法和高效液相色谱法等。2005版《中国药典》[1]以中性乙醇为溶剂、酚酞为指示剂，用NaOH滴定其含量，步骤繁琐，误差较大；高效液相法[2–3]测量结果精确度高，但分析时间较长。

拉曼光谱分析具有无损性、监测灵敏度高、检测时间短等优点，使用光纤探头无需取样就能够快速采集阿司匹林合成体系的拉曼信息,可对多组分进行同时测定[4]。由于待测组分在拉曼光谱数据中有多个特征峰位[5]，各个待测组分与它们的特征峰位的光谱数据之间存在交迭现象，很难分离出某个特征峰以便对其组分浓度进行定量分析，因此拉曼光谱分析需要用到多元校正技术[6–7]以克服多重相关性造成的信息重叠，解释体系内的综合变量，区分反应组分信息与背景噪声。已知组分的回归预测即对白色体系的回归预测[8]，主成分回归和偏最小二乘法都可以提取组分变量的特征信息[9]，而后者进行光谱矩阵分解时考虑了待测属性矩阵的信息，使得显著包含待测属性特征的光谱区有更大的权重。Thomas等人[10]对经典最小二乘 (PLS)、主成分回归和偏最小二乘在定量校正中应用进行了比较，认为偏最小二乘是对组分预测最优的方法。

由于拉曼光谱易受监测环境的影响，在采集拉曼光谱过程中光程变化以及光程中介质变化都会引起光的吸收变化造成基线漂移[11]。因此为了提高分析准确度，经常在回归之前要对光谱进行预处理，降低背景干扰，除去部分噪声提高信噪比。通常的预处理方案[12–14]有均值中心化标准化、归一化、标准正态变换及去趋势、平滑及求导等。

1 实验部分

1.1 主要仪器与试剂

水杨酸、乙酰水杨酸、乙酸酐、乙酸：分析纯；

激光发射器：Laser-785型，美国Danger公司；

拉曼光谱仪：科研级，QE65000型，美国Ocean optics公司；

光纤探头：BAC100–785–OEM 型，美国 Ocean optics公司；

电子分析天平：ALC–210.4型，德国Acculab公司；

1.2 溶液制备和拉曼信息的采集

1.2.1 标准溶液的制备

阿司匹林合成路线见图1。

图1所示阿司匹林的合成体系中主要为5个组分，分别为阿司匹林、水杨酸、乙酸、乙酸酐、催化剂(浓硫酸或氨基磺酸)。其中变量为4个：阿司匹林、水杨酸、乙酸、乙酸酐，假设反应结束水杨酸反应完全，则反应前后的水杨酸–乙酸酐–阿司匹林的当量比分别为n∶2n∶0和 0∶n∶n，配制41个样本溶液。水杨酸、乙酸酐、阿司匹林3组分物质的量的范围分别为 5～0 mmol；10～5 mmol；0～5 mmol，隔0.125 mmol递减和递增,用乙酸定容至10 mL。

1.2.2 拉曼信息的采集

以波长785 nm激光作光源，通过BAC100–785–OEM光纤探头收集拉曼信息，对ocean optics spectrasuite工作站菜单选择x轴单位设置为拉曼位移，积分时间选择是1／s，获取拉曼光谱波长范围为0～2000 cm–1。将41个标准溶液分别倒入光程为1 cm石英比色皿中采集实验样本的光谱数据并保存。

2 数据处理与讨论

2.1 训练样本集制备

在41个样本中从第3个样本到第39个样本每隔4个样本选取10个样本作为检验集，剩余作为校正集。从图2中可看出，41个样本的拉曼光谱交迭并且存在基线漂移，拉曼光谱漂移较为明显的一条为预测集第5个样本。

2.2 PLS 回归

选取全波长范围的原始数据进行PLS回归。主成分即引起光谱变化的样本主要变量为阿司匹林、水杨酸、乙酸、乙酸酐。变量数目为4，交叉验证方法“逐一法”对检验集回归，原始数据PLS检验集结果及评价如图3所示。

由图 3(a)，(b)，(c)中检验集的水杨酸、乙酸酐、阿司匹林原始数据PLS回归结果的真实值与预测值相关图可以看出，多数样本点的残差杠杆都在回归线附近均匀分布，第5个样本点出现高杠杆。图3(d)中多数样本分布在Q和T2的可信区间内，第5个样本为异常值[QResidual=1.25×107>(95.0%limit=4.34×105)，HotellingT2=678>(95.0% limit=12.1)，差异显著]，其差异可认为是由系统误差造成的。由图2训练样本拉曼光谱可看出，此样本拉曼光谱明显漂移造成回归残差较大。

3.3 原始数据PLS回归模型及经预处理的PLS回归模型评价

3.3.1 拉曼光谱预处理方案选择

为了减小因光程变动而造成的基线漂移的影响，增强样本光谱以及浓度的差异性，经试验选定回归结果较好的5种光谱预处理方案，表1中A到F为原始光谱和所选定的5种光谱预处理方案。

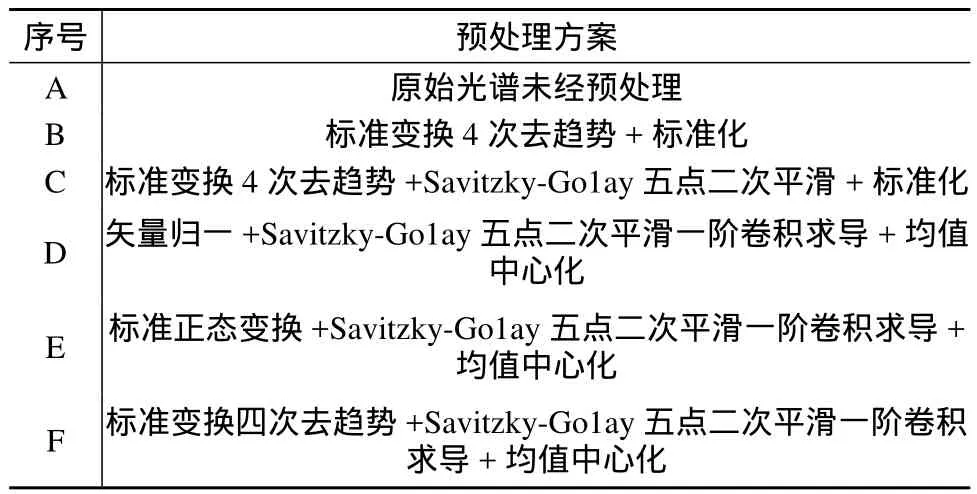
表1 拉曼光谱预处理方案

3.3.2 校正集PLS评价

原始光谱与所选五种光谱预处理方案校正集中回归结果比较，校正集称量值与拟合值相关系数R2、校正均方根误差RMSEC、交互验证均方根误差RMSECV如表2所示。

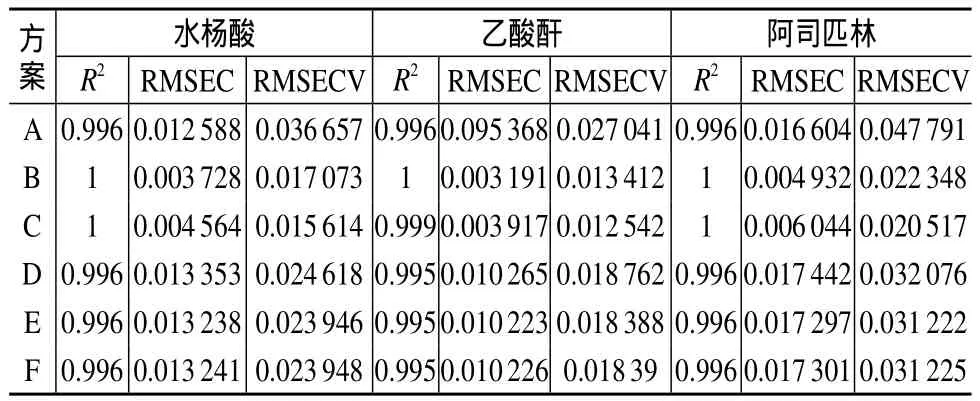
表2 校正集PLS回归结果评价

表2中方案B用标准正态变换再经过标准化后，校正集的相关系数，校正均方根误差和交互验证均方根误差与方案A原始数据有明显改善，方案C在方案B的基础上中间增加了Savitzky-Go1ay五点二次平滑处理，校正均方根误差有所增加，但交互验证均方根误差减小。方案D，E，F经Savitzky-Go1ay点二次平滑一阶卷积求导校正集中线性系数和校正均方根误差与方案A原始数据比较并没有变化，交互验证均方根误差略有降低。

3.3.3 检验集PLS评价与方案确定

原始光谱与所选5种光谱预处理方案预测集中回归结果比较，检验集称量值与拟合值相关系数R2、预测均方根误差RMSEP如表3所示。

表3 检验集PLS回归结果评价

表3中方案B～F检验集中相关系数和预测均方根误差与方案A原始数据比较都有很好的改善；方案B标准正态变换再经过标准化后，检验集的线性系数，预测均方根误差有明显改善；方案C在方案B的基础上增加了Savitzky-Go1ay五点二次平滑处理，检验集的线性系数，预测均方根误差较方案C有所改善；方案D，E，F经Savitzky-Go1ay五点二次平滑一阶卷积求导预测集中线性系数和预测均方根误差较为满意，方案D中虽然阿司匹林的相关系数较方案E和方案F低，但乙酸酐的线性系数有所提高，并将预测均方根误差降至最低分别为0.00815，0.010265，0.011101。

由上述结果对此模型选定预处理方案为D矢量归一+Savitzky-Go1ay五点二次平滑一阶卷积求导+均值中心化，主成分选4，采用“逐一法”对模型进行回归结果如图4所示。

经矢量归一+Savitzky-Go1ay五点二次平滑一阶卷积求导+均值中心化对拉曼光谱预处理再进行PLS回归，由图4(a)，(b)，(c)中检验集的水杨酸、乙酸酐、阿司匹林真实值与预测值相关图可以看出，几乎所有样本点的残差杠杆都在回归线附近均匀分布，没有出现明显的高杠杆。(d)中多数样本分布在Q和T2的可信区间内，第5个样本的QResidual(0.000124)大于 95.0% limit(8.32×10–6)存在异常，HotellingT2=10.3<(95.0% limit=12.1)，此差异是偶然误差引起的正常差异，故此预处理方案可以采用。

综上所述，虽然QResidual=0.000124超过了Q的可信区间 (95.0% limit=8.32×10–6)，HotellingT2=10.3在T2的可信区间(95.0% limit=12.1)被认为是偶然误差不可避免，再综合检验集R2和RMSEP，回归结果较为满意。

4 结论

经标准正态变换Savitzky-Go1ay五点二次平滑再标准化后虽然对校正集自身拟合的程度很好，对检验集却不如经过Savitzky-Go1ay五点二次平滑一阶导数的拟合效果好。经过Savitzky-Go1ay五点二次平滑一阶导数的拟合结果交互验证均方根误差有所改善，并且对外部检验集有理想的拟合效果。较大程度减小了由光谱监测环境的影响和光程变化以及光程中介质变化引起基线漂移。

对于此分析模型，采用矢量归一+Savitzky-Go1ay五点二次平滑一阶卷积求导+均值中心化对拉曼光谱预处理，PLS主成分选4，交互验证选用“逐一法”可对阿司匹林反应体系3组分进行同时测定，可应用于阿司匹林合成体系在线浓度的测量，为后续质量预测、动态优化控制工作提供了有力的数据支持。

[1]国家药典委员会.中华人民共和国药典[M].2部.北京: 化学工业出版社，2005: 283.

[2]李克庆.测定阿司匹林肠溶衣片中阿司匹林含量及游离水杨酸中国药师，2006，9(10):925–927.

[3]Hiral J Panchal，Bhanubhai N Suhagia，Natvarlal J Patel，et al. Simultaneous Estimation of Atorvastatin Calcium，Ramipril and Aspirin in Capsule Dosage Form by RP–LC[J].Chromatographia，2009，69(1): 91–95.

[4]李卫华，吕国华，黄兰，等.阿司匹林合成过程的在线拉曼光谱研究[J].物理化学学报，2003，19(2): 105–108.

[5]Murty G V L N，Seshadri T R. Raman effect and hydrogen bonds Part IX. Solutions of salicylic acid and aspirin[J]. Proceedings Mathematical Sciences，1944，19(1): 17–20.

[6]Cooper J B. Chemometric analysis of Raman spectroscopic data for process control applications[J]. Chemometrics and Intelligent Laboratory Systems，1999，46(2): 231–247.

[7]Estienne F，Massart D L，Zanier-Szydlowski N，et al. Multivariate calibration with Raman spectroscopic data: a case study[J].Analytica Chimica Acta，2000，424(2): 185–201.

[8]梁逸曾.白灰黑复杂多组份分析体系及其化学计量学算法[M].长沙: 湖南科学技术出版社，1996: 29–36.

[9]Estienne F，Massart D L. Mutlivariate calibration with Raman data using fast princip component regression and partial least squares methods[J]. Analytica Chimica Acta，2001，450(1–2): 123–129.

[10]Edward V T，David M H. Comparison of multivariate calibration methods for quantitative spectral analysis[J]. Analytical Chemistry，1990，62(10): 109l-1099.

[11]Andrade J M，Garrigues S，de la Guardia M，et al. Nondestructive and clean prediction of aviation fuel characteristics through Fourier transform-Raman spectroscopy and multivariate calibration[J]. Analytica Chimica Acta，2003，482(1): 115–128.

[12]史永刚，冯新泸，李子存.化学计量学[M].北京: 中国石化出版社，2002: 141–143.

[13]Wu W，Guo Q，Jouan-Rimbaud D，et al. Using contrasts as data pretreatment method in pattern recognition of multivariate data[J].Chemometrics and Intelligent Laboratory Systems，1999，45(1–2):39–53.

[14]Peter A G. General least-squares smoothing and differentiation by the convolution (Savitzky-Golay)method[J]. Anal Chem，1990，62(6): 570–573.