湍流入流条件在强迫转捩研究中的应用
2012-08-21逯学志黄章峰罗纪生
逯学志,黄章峰,2,罗纪生
(1.天津大学力学系,天津300072;2.空气动力学国家重点实验室,四川 绵阳621000)
0 引 言
直接数值模拟(Direct Numerical Simulation,DNS)可提供流场的高分辨率的全部信息,是研究湍流机制的主要工具之一,尤其是对超声速和高超声速边界层流动。然而采用空间模式的直接数值模拟(Spatial Direct Numerical Simulation,SDNS),其入流条件应能反映上游的特性,对于湍流计算而言入流条件如何给是一大难题。本文介绍了一种新的提法,即将由时间模式直接数值模拟(Temporal Direct Numerical Simulation,TDNS)得到的充分发展湍流流场(只需要一个时刻的流场)以适当方式转换成SDNS的入口流场。计算结果证实该方法可行且有效。
对于高超声速飞行器,下表面往往有两到三个压缩折角,飞行器下部的气流经过这些压缩折角后进入发动机。如果折角处流动状态为层流状态,往往会在折角处发生流动分离,从而导致气流偏离下表面,只有较少部分的气体流入了发动机,严重影响了发动机的性能。然而在边界层的前部,流动一般是层流,而且自然状态下层流段可以很长。这时为使转捩提前,需要采用加人工粗糙度的方法,使之在第一个压缩折角前就发生强迫转捩。
美国主要采用地面试验和飞行试验的验证方法来研究各种转捩装置的效果[1-3],并通过传热系数是否快速上升来判断人工粗糙度促使转捩是否成功。但实际上,实验和数值模拟结果表明,由于壁面粗糙引起的流向涡也会导致St上升[4-5],如图1所示,其趋势和由于转捩导致的很相似。其中St的定义为:因此传热系数上升既可能是由于转捩导致的,也可能是由于较强的流向涡引起的,不是强迫转捩后达到湍流状态的可靠判据。有必要对添加湍流发生器后下游流场是否真的达到了湍流状态进行研究。
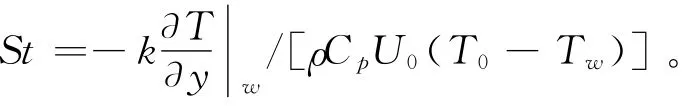

图1 由于壁面粗糙引起的流向涡导致传热系数St曲线上升Fig.1 Increasing of St led by stream-wise vortex caused by the wall roughness
本文利用充分发展湍流的相似性特性和可维持特性来研究强迫转捩发生的可能性。采用空间模式直接数值模拟(SDNS)的方法,在入口处添加包含湍流信息的扰动,如果在下游流场能够恢复湍流状态,说明强迫转捩有可能发生,此时入口扰动与湍流信息存在一定的关系;如果在下游流场趋近层流状态,说明即使是在入口添加了包含湍流信息的扰动也无法达到湍流状态,强迫转捩很有可能不会发生,此时需要考虑更下游的位置。
1 数值方法
1.1 时间模式直接数值模拟
DNS的控制方程为无量纲的守恒型的N-S方程,不做任何假设。在结构化的网格上采用有限差分法进行空间离散,并采用高精度的紧致差分格式计算;时间上采用满足TVD(Total Variation Diminished)特性的高阶Runge-Kutta方法离散;为了使用迎风差分格式,对非线性项还根据Jacobian矩阵特征值的正负进行通量分裂。除了给出合理的初始条件外,还需要给定边界条件。对于边界层流而言,在流向和展向均为周期性边界条件,而在法向,一个是固壁一个是出流条件。
采用时间模式直接数值模拟(TDNS)的好处是计算量小,可以一直从层流计算到充分发展湍流;其缺点是流向存在局部平行流假设。研究结果表明,对于零压力梯度的高速平板边界层,其雷诺数很大,空间模式直接数值模拟(SDNS)和TDNS的计算结果相比,在定性和定量上的差别都很小[6]。
1.2 空间模式直接数值模拟
与TDNS不同,空间模式直接数值模拟(SDNS)在流向还需要入流条件,而入流条件应能反映上游的流动特性。对于湍流计算而言,入流条件如何给是一大难题。
1.3 采用TDNS结果作为SDNS的入流条件
采用TDNS在某一时刻的结果,这时有确定的边界层厚度,有相应的Reynolds数。利用充分发展湍流的相似性特性,对TDNS在某一时刻的结果在法向进行相似变换,就可以得到指定Reynolds数下的流场,这一流场的Reynolds数也就是SDNS入口处的Reynolds数。
转换的步骤如下[7-8]:(1)采用 TDNS计算得到零压力梯度的平板边界层的充分发展湍流流场,取某一时刻的结果XT(x,y,z),其湍流边界层厚度为δT;(2)采用数值方法求出具体问题的层流解Xc(x,y,z),其计算域入口的层流边界层厚度为δC;(3)假定流体在计算域入口处之前刚刚完成转捩,则在计算域入口已是湍流,其边界层厚度变为kδδC,其中kδ取2到3.5;(4)将TDNS的结果在法向做相似变换XT(x,z),其中=ykδδC/δT,并分解为平均量与脉动量之和;(5)在湍流边界层内采用TDNS的平均流场,在湍流边界层外采用SDNS的层流解 Xc(x0,y,z),中间采用光滑函数进行连接,从而得到SDNS入口处的平均流场;(6)以适当方式将TDNS的脉动量X′T空间分布转换成SDNS所需的入口流场的时间序列,从而得到SDNS入口处的脉动流场。
转换的示意图如图2所示。将转换关系写成x=ct,其中x的原点在TDNS中流场的出口处,方向朝向上游。这样做的基本概念是流场中x处的扰动以速度c向下游传播,在t时刻将到达出口处,而这正好可以作为SDNS的入口扰动。当x的值大于TDNS的流向计算域长度后,可利用流向周期性边界条件的性质,减去流向计算域长度即可。这里取c=0.92[7]。
该方法已经被证实是解决空间模式直接数值模拟(SDNS)入口条件的一种有效方法,并且对不同Mach数、Reynolds数、壁面条件、典型边界层类型均可行[7-8]。
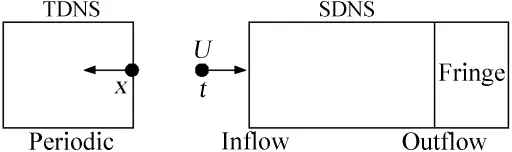
图2 由TDNS得到的某时刻充分发展湍流流场转换成SDNS的入口流场的示意图Fig.2 Schematic diagram of the transformation from TDNS to SDNS
2 物理模型和计算工况
2.1 二维层流解的计算
本文选取某高超声速飞行器的对称面作为研究对象,物理模型的头部为圆弧,下表面有三个坡道。计算域如图3所示。以来流速度U0=1789m/s和头部半径r=2.5mm为基本参量进行无量纲化,无量纲参数Ma=6,单位Re=5.0×106,攻角为0°。采用SDNS的方法计算得到二维层流解,其网格参数为:流向2300个点;法向201个点,头部激波内部的点数不少于170个,靠近壁面的1个边界层名义厚度内的点数不少于75个,距离壁面最近的网格尺度不超过0.002个无量纲长度。
2.2 三维流场的计算
截取二维SDNS中下表面某坡道内的层流流场,并在展向做扩展,作为三维SDNS的层流解,其中x方向沿着壁面向右,y方向垂直壁面向下,z方向垂直xy平面向外。三维SDNS中的入口位置是指入口壁面处在二维SDNS计算域的x坐标值(图3(b)所示),流向长度指x方向的长度,展向长度指z方向的长度,为21个无量纲长度,有128个网格点。本文选取文献[7]中的平板湍流边界层TDNS的结果,结合SDNS入口处层流边界层厚度,按照1.3节给出三维SDNS的入流条件。
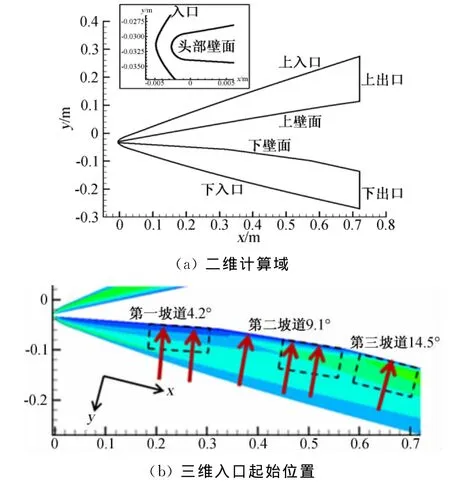
图3 计算域示意图Fig.3 Schematic diagram of computational domain
2.3 计算工况
在下表面某位置添加湍流发生器后,此湍流发生器为下游流体提供了有限幅值的扰动,有可能导致强迫转捩。如果在下游某个位置发生了转捩,那么在转捩后的湍流流场应该能够维持湍流状态。
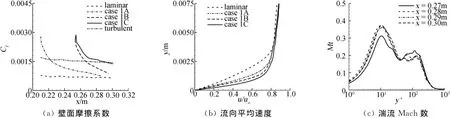
图4 第一个坡道的计算结果Fig.4 Results in the first ramp
入口处的不同位置代表湍流发生器的不同位置,入口处加扰动的强度代表发生器不同的形状;通过考察湍流的可维持特性来研究湍流发生器对流场的影响,如果在入口引入湍流信息后,流场很快能调整到湍流状态,说明在计算域内通过加湍流发生器能够达到湍流状态,否则在计算域范围内难以达到湍流状态。本文考察了入口处不同位置和不同湍流度的情况,共9种情况,详情见表1,其中最大脉动速度均方根是指三个方向脉动速度的平方和的均方根沿法向剖面的最大值。

表1 计算工况Table 1 Computational cases
3 结果分析
3.1 第一个坡道的结果
图4(a)和图4(b)给出了第一个坡道内3个算例的壁面摩擦系数沿流向的分布、流向平均速度剖面在靠近出口处沿法向的分布。可以看出,情况A和B的壁面摩擦系数逐渐减小,并趋近于层流状态的值,而且入口位置越靠前,越趋近层流解。从图4(b)可以看出,三种情况的平均速度剖面不同程度地偏离了层流解,并且入口位置越靠前、入口湍流脉动幅值越小,平均速度剖面越不饱满。这表明在第一坡道内引入较小幅值的扰动,流场会趋近于层流状态。
情况C中的壁面摩擦系数在x=0.28m之前是快速减小,而在之后减小的幅度较小,并且其幅值接近湍流状态的幅值。此外在情况A、B和C三种的流向平均速度剖面来看,情况C的流向平均速度剖面最饱满,有可能是湍流状态。
图4(c)给出了第一个坡道内情况C中不同位置的湍流Mach数沿法向的分布,可以看出在x=0.28m之后的湍流Mach数几乎重合。根据湍流的相似特性,说明此时流场达到了湍流状态。这表明在第一坡道内引入较大幅值的扰动,流场有可能趋近湍流状态,强迫转捩有可能发生。
3.2 第二个坡道的结果
图5(a)和图5(b)给出了第二个坡道内3个算例的壁面摩擦系数沿流向的分布、流向平均速度剖面在靠近出口处沿法向的分布。可以看出,添加扰动的入口位置越靠后,壁面摩擦系数偏离层流解越多,平均速度剖面越饱满。当扰动的脉动速度均方根值最大值不小于0.15时,下游的流场均趋近湍流状态。
图5(c)给出了第二个坡道内情况C中不同位置的湍流Mach数沿法向的分布,可以看出在x=0.54m之后的湍流Mach数也同样具有相似性。这一点与图5中情况C中x>0.54m时壁面摩擦系数较平缓减小的结论是一致的,说明此时流场达到了湍流状态。

图5 第二个坡道的计算结果Fig.5 Results in the second ramp
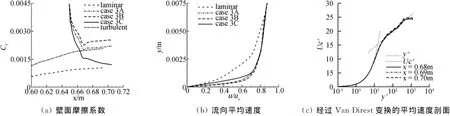
图6 第三个坡道的计算结果Fig.6 Results in the third ramp
3.3 第三个坡道的结果
图6 (a)和图6(b)给出了第三个坡道内3个算例的壁面摩擦系数沿流向的分布、流向平均速度剖在靠近出口处沿法向方向的分布。可以看出在入口处添加湍流较大幅值扰动后,经过一个快速的调整段,壁面摩擦系数在x=0.67m开始趋近湍流状态的值,但如果扰动的幅值较小,壁面摩擦系数任然会趋近于层流状态的值。从流向平均速度剖面同样也可以看出,情况A和B的剖面很饱满,而情况C的剖面在靠近壁面处趋近于层流解。
图6(c)给出了第三个坡道内情况B中经过Van Direst变换的平均速度剖面,可以看出在x=0.68m到x=0.70m的平均速度剖面几乎重合,符合平均速度的相似性特性。并且平均速度剖面与线性律和对数律都吻合的很好,说明情况B确实达到了湍流状态。
4 结 论
采用空间模式直接数值模拟的方法,仿真了带有三个压缩折角的高超声速飞行器下表面的湍流发生器,分析了其引起强迫转捩的可能性,发现:
(1)在第一个坡道内不会发生自然转捩。
(2)在第一个坡道上,扰动脉动速度均方根值小于0.15时,流场趋近于层流状态,不会发生强迫转捩;如果大于0.225时,流场有趋近湍流状态的趋势,有可能发生强迫转捩。
(3)在第二个和第三个坡道上,扰动脉动速度均方根值为0.15时,流场趋近湍流状态,有可能发生强迫转捩,但如果小于0.03时,流场有趋近层流状态的趋势,不会发生强迫转捩。
[1] TIRTEY S C,CHAZOT O.Characterization of hypersonic roughness induced transition for the EXPERT flight experiment[R].AIAA 2009-7215.
[2] BERRY S,DARYABEIGI K.Preliminary analysis of boundary layer transition on X-43Aflight 2[A].52nd JANNAF Propulsion Meeting[C],2004.
[3] BERRY S,DARYABEIGI K,WURSTER K.Boundary layer transition on X-43A[R].AIAA 2008-3736.
[4] LIU J T.Nonlinear instability of developing stream-wise vortices with applications to boundary layer heat transfer intensification through an extended Reynolds analogy[J].Phil.Trans.R.Soc.A.,2008,366:2699-2716.
[5] MOMAYEZ L,DUPONT P,PEERHOSSAINI H.Some unexpected effects of wavelength and perturbation strength on heat transfer enhancement by Go¨rtler instability[J].International Journal of Heat and Mass Transfer,2004,47:3783-3795.
[6] 黄章峰,曹伟,周恒.超声速平板边界层转捩中层流突变为湍流的机理--时间模式[J].中国科学(G 辑),2005,35(5):537-547.
[7] 黄章峰,周恒.湍流边界层的空间模式DNS的入口条件[J].中国科学(G辑),2008,38(3):310-318.
[8] 董明,周恒.超声速钝锥湍流边界层DNS入口边界条件的研究[J].应用数学和力学,2008,29(8):893-904.
