基于改进微分进化算法的电力系统无功优化

徐志成，钱金法（常州机电职业技术学院，江苏 常州 213164）

1 引言

无功优化是电力系统经济运行最重要的手段之一，常用的方法包括灵敏度法、非线性规划法、内点法等。这些方法通常需要使用梯度矢量信息，这使得在求解具体问题时不得不做一些近似处理，因为在电力系统无功优化中存在较多离散变量；同时，无功优化问题又是一个多约束优化问题，将这些约束条件同时考虑时，就不能保证其性能指标是一个凸函数，而有可能是一个多峰值的函数，以上几种方法都是基于单点的搜索方法，很容易由于初始点的选取不当而陷入局部极值区。

近年来，遗传算法、免疫算法等现代启发式寻优方法在无功优化方面做了大量的研究[1-4]，弥补了传统数学方法的不足。基于遗传算法的无功优化方法有许多优良特性，能找到近似的全局最优解。但是该算法缺点是计算时间长[3-5]，很难满足实际运行的需要，其主要原因是遗传算法局部搜索能力差，容易出现早熟而收敛到局部最优解[5-7]。采用自适应等改进的遗传算法可以改善算法性能[5-6]，但并没有完全解决这些问题，目前的遗传算法仍然存在计算速度慢的问题。加快算法的收敛速度，改善算法解的质量是目前研究的重点。

学者Stron和Price针对实参数优化问题提出了微分进化(differential evolution)算法[7-10]，其主要特点是收敛速度快、可调参数少、鲁棒性好、算法简单，近些年逐渐被人们所接受，成为研究的热点之一。本文在对基本DE算法进行改进的基础上，利用其强大的寻优能力来进行电力系统无功优化研究，并针对实际对象进行了仿真实验。

2 DE算法

2.1 初始化

同GA、PSO等进化算法一样，在寻优时需要对种群数量的大小及初始种群进行生成。通常，初始种群的生成方法是从给定边界约束内的值中随机选择，应该覆盖整个参数空间。而种群数量Np一般取10倍于所求解问题规模的维数。设第i个个体Xi=(xi，1,xi，2,…,xi，n)，Xi∈Rn，n为问题解空间的维数，初始种群s= {X1,X2,…,XNp}，为个体的集合。一般个体向量Xi各个分量的产生方式为

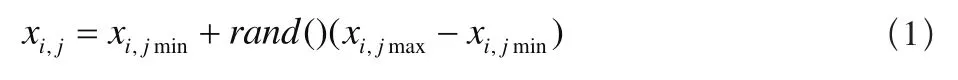
式中xi,j、xi,jmax、xi,jmin分别为个体向量Xi的第j个分量及第j个分量的上下限。

2.2 变异

对于第k+1代每个目标向量，基本DE方法变异向量产生方式为：

2.3 交叉

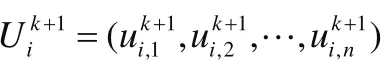
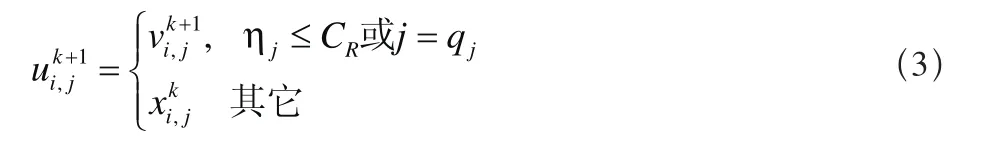
式中：qi是从[1，n]中随机选取的一个整数，用以保证本次操作必须有一位经过交叉；ηj∈[0,1]是针对第j维分量随机选取的控制参数；交叉因子CR∈[0,1]为算法参数，需要事先确定，其控制着种群的多样性，帮助算法从局部最优解中脱离出来。

2.4 选择

在标准DE方法中，使用“贪婪”选择模式：当且仅当新个体的评价函数值更好时，才被保留到下一代群体中，否则，父个体仍然保留在群体中，再一次作为下一代的父向量。

2.5 DE的控制参数

控制参数的选择对DE算法的搜索性能有较大的影响，根据经验，种群数量Np可选择在5～10倍的问题维数之间，但Np必须大于4以确保DE具有足够的不同变异向量。比例因数F和交叉因数CR在进化过程中的取值区间一般分别是[0.4，0.9]和[0.3，0.8]，它们的优化值往往依赖于目标函数的特性。

2.6 DE算法的改进

在DE算法中，控制参数的合理设置是一个十分困难的问题，许多学者对此问题作了专门的研究，使得DE参数的控制策略有了很大的提高，但一般采用进化代数作为参数动态调整依据[8]。一般来说，F和CR不能过小，以避免算法过早收敛，较大的F和CR增加了算法从局部最优逃脱的可能性。然而，若F>1，则算法的收敛速度会明显降低，这是因为当扰动大于群体内两个成员间的距离时，收敛会非常困难。由式(2)可见，在搜索的初始阶段，由于个体随机分布在解空间中，因此向量的差值比较大，这时要求算法的控制参数F相对小一些；随着种群的不断进化，各个个体逐渐靠近最优个体，算法中的变异操作产生的差向量会逐渐变小，在一定程度上减弱了算法搜索空间的多样性，因此要求此时的控制参数F相对大一些，使得变异操作后的向量能够开拓新的搜索空间，从而提高算法的全局寻优能力。同样，对交叉因子来说，过小的CR使得算法的种群在交叉操作后产生较少的新个体，这样就减弱了算法开拓新空间的能力；而过大的CR使得种群不能较好地保持稳定，降低了算法的稳定性。

由式(2)可见，要对算法参数较好的进行控制，就要动态掌握种群的个体分布情况，根据个体的分布，确定合适的控制参数。在进行寻优的过程中，群体适应度方差是一个能够较好体现当前个体与最优点的分布情况的量化指标，计算方便，适合用来对控制参量进行动态调整，适应度方差计算如下：

式中，Np为种群数量；fi为第i个个体的适应度；fav为种群的平均适应度；fbest为群体最佳适应度。由式(4)可见，适应度方差的取值范围在[0，Np]，群体适应度方差 σ2越小，群体聚集程度越高；反之，则群体个体分布越分散。考虑种群分布情况后，DE算法的第k代控制参数自适应调整策略为：

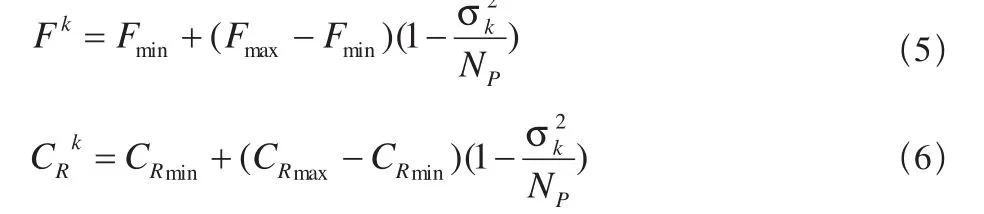
式中，Fmax、Fmin为差分因子F的上下限；CRmax、CRmin为交叉因子CR的上下限。

3 基于改进DE算法的电力系统无功优化

3.1 问题描述

电力系统实现无功功率的优化调度与控制，可以改善系统的电压质量，减少电能传输损耗。无功优化的目的是通过调整无功潮流的分布降低有功网损，并保持最好的电压水平，因此，目标通常是有功损耗最小，即

PL为系统的有功损耗，其表达式为：

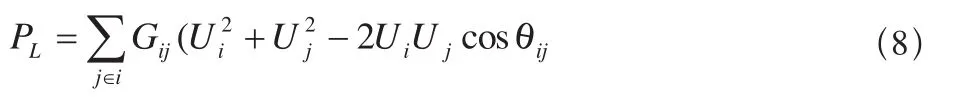
式中，Ui、Uj为节点i、j电压；θij为节点i电压和节点j电压的相位角之差；Gij、Bij为节点导纳矩阵中元数的实部和虚部。

等式约束条件为：

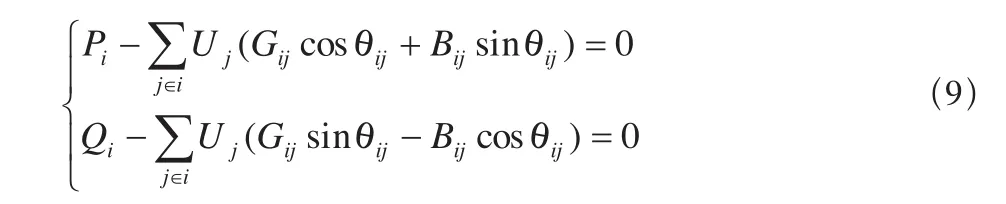
式中，Pi、Qi为节点i注入的有功和无功功率；

不等式约束条件为：

式中，Uimax和Uimin为PQ节点i的电压幅值上下限；Qimax和Qimin为 发电机节点i无功出力上下限；QCi、QCimax、QCimin为无功补偿装置节点i投切量及其上下限；KTi、KTimax、KTimin为有载可调变压器i变比及其上下限；UGi、UGimax、UGimin为PV节点发电机机端电压幅值及其上下限。

为了方便与文献[11]比较，本文取（11）式作为无功优化目标函数:

λuPu为PQ节点电压越限的惩罚项，λu为惩罚因子，Pu的表达式为：

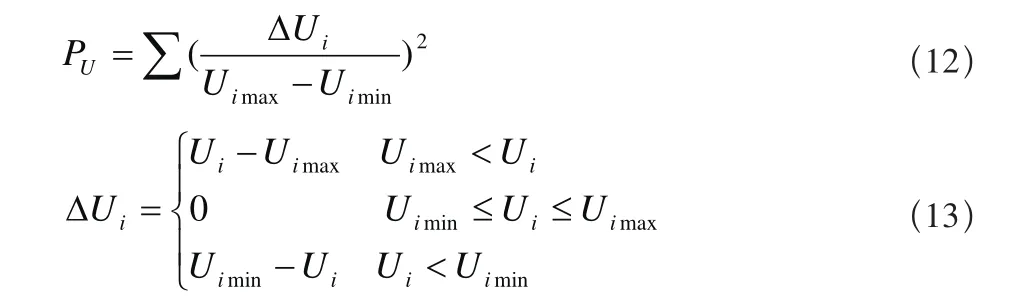
λQPQ为PQ节点无功越限的惩罚项，λQ为惩罚因子，PQ的表达式为：

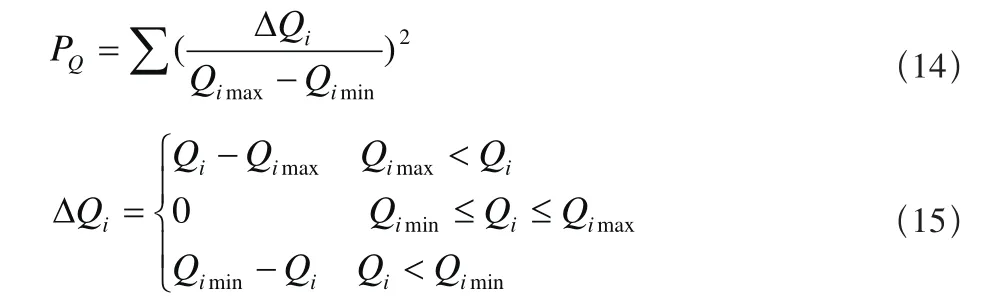
采用本文算法进行无功优化时，位置x(k)的各维变量由无功优化问题中的控制变量UG、KT、QC组成，即

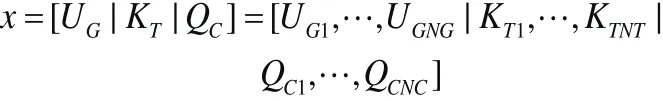
发电机电压UG的取值范围为[0.9 1.1]，且是连续的；变压器档位KT的取值范围为[0.9 1.1]，间距为0.02；电容器无功QC的取值范围为[-0.1 0.1]，间距为0.02。

3.2 实例仿真

以IEEE30节点系统为例，用MATLAB7.0编程，对上述模型和方法进行验证。系统具有30个节点、6台发电机、4台可调变压器。节点电压变化范围均为0.94～1.06p.u.。有载调压变压器的档位范围均为1±8×0.0125。系统在节点10、24处分别配置了可投切电容器组，节点10处并联电容器组电纳可调上限为0.50p.u.，分段步长0.10p.u.，节点24处并联电容器组电纳可调上限为0.10p.u.，分段步长0.02 p.u.。

为了进一步说明本文方法的有效性，本文同时采用PSO算法，并与文献[11]中二次变异遗传算法（SMGA）的结果相比较。

方便于比较三种算法的性能，与文献[11]相同，三种算法的收敛条件为：连续8代目标函数值没有减小并且计算代数大于设置的最小代数。在满足不等式约束的条件下，计算100次进行统计。计算代数统计见表1；100次计算中最好、最差和平均网损统计见表2；优化的网损分布区域统计见表3。

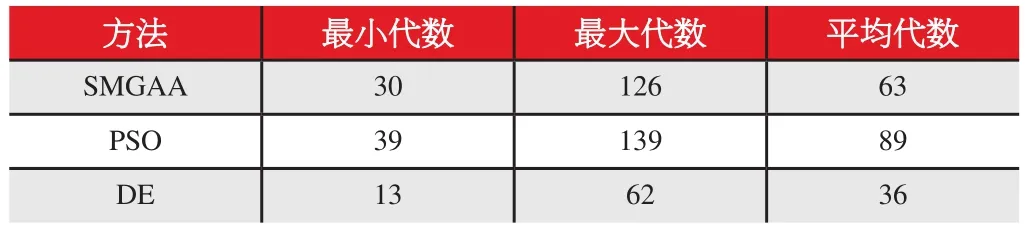
表1 计算代数统计

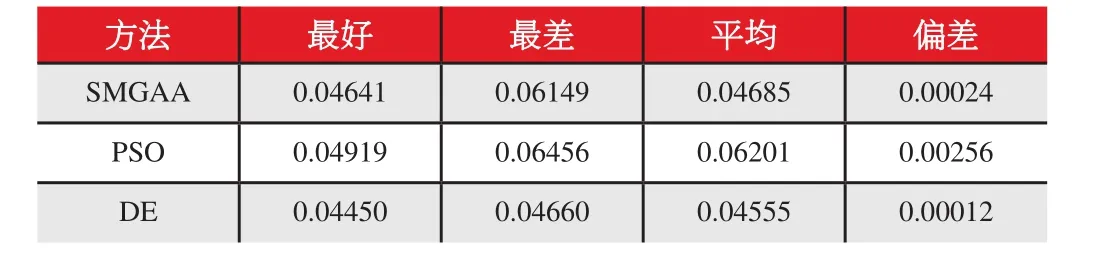
方法 最好 最差 平均 偏差SMGAA 0.04641 0.06149 0.04685 0.00024 PSO 0.04919 0.06456 0.06201 0.00256 DE 0.04450 0.04660 0.04555 0.00012

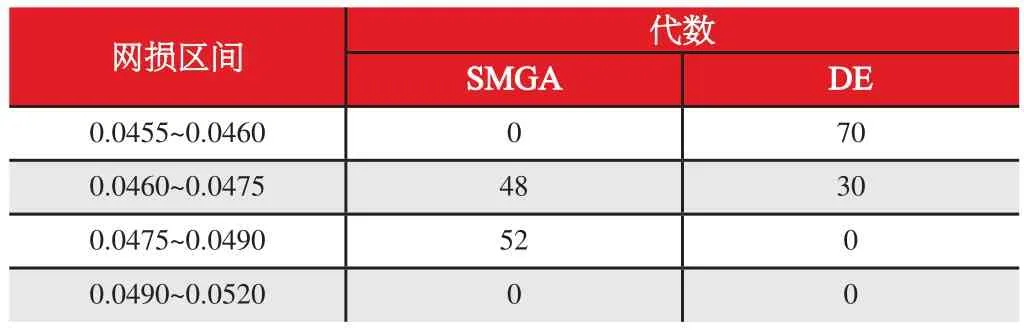
表3 网损分布区域统计

从表1可以看出，文献[11]中提出的二次变异遗传算法(SMGA)用于电力系统无功优化，其计算最小代数为30，最大代数126，平均代数63；运用PSO算法，其计算最小代数为39，最大代数139，平均代数89；而运用本文提出的方法，其计算最小代数为13，最大代数62，平均代数36。可以看出，本文方法的收敛速度远远高于上述两者方法。

从表2可以看出，SMGA算法的优化结果分布在0.04641～0.0490p.u.区域，最好和最差网损相差2.25%；本文方法的结果分布在0.0455～0.0460p.u.区域，最好网损和最差网损相差2.55%。可以看出，本文方法得到的平均网损和标准偏差均比SMGA算法、PSO算法小，本文方法的寻优性能更好，且优化结果更集中，可见运用本文方法能搜索到更好的优化解，其解的质量更高，本文方法的标准偏差低于SMGA算法和PSO算法，说明本文方法更具有稳定性。

从表3数据可以看出，SMGA算法的优化结果分布在0.0460～0.0490p.u.之间；本文方法的优化结果分布在0.0455～0.0475p.u.之间，这说明本文方法优化结果比SMGA算法更加集中在小的区域并且集中在网损小的一端， 同样说明本文方法较SMGA算法的寻优性能及稳定性更好。

4 结语

无功优化在电力系统经济运行中占有重要的地位，对其进行研究具有重要的现实意义。DE算法是一种基于群体优化的全局搜索方法，可有效解决无功优化这类非线性混和整数优化问题。通过对IEEE30节点系统的仿真分析表明，DE比GA以及PSO算法的搜索性能更好，能在较短的搜索时间内找到更接近于全局最优解。

[1]DAS D B, PATVARD HAN C. Reactive power dispatch with a hybrid stochastic search technique[J].Electric Power Energy System,2002,24(9):731-735.[2]许文超,郭伟. 电力系统无功优化的模型及算法综述[J].电力系统及其自动化学报, 2003,15(1):100-104.

[3]郭创新,朱承治,赵波,等.基于改进免疫算法的电力系统无功优化[J].电力系统自动化,2005,29(15):23-29.

[4]万黎,袁荣湘.最优潮流算法综述[J].继电器,2005,33(11):80-87.

[5]钟红梅,任震,张勇军,等.免疫算法及其在电力系统无功优化中应用[J].电网技术,2004,28(3):16-19.

[6]LAI L L, MAJ T. Application of evolutionary programming to reative power planning comparison with nonlinear programming approach[J]. IEEE Trans on Power System, 1997,12(1):198-204.

[7]Stron R, Price K. Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[R]. Technical Report TR-95-012, ICSI, 1995.

[8]Stron R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization,1997,11:341- 359.

[9]Stron R, Price K. Minimizing the real functions of the ICEC 96 contest by differential evolution [C]. IEEE Conference on Evolutionary Computation,Nagoya, 1996: 842-844.

[10]Junhong Liu, Jouni Lampinen. A fuzzy adaptive differential evolution algorithm[C]. Proceedings of IEEE Tencon’02. Beijing, China,2002:606- 611.[11]康积涛,钱清泉. 电力系统无功优化的二次变异遗传算法[J]. 电力自动化设备, 2007,27(9):7-11.

★ [基金项目]：国家自然科学基金资助项目（60421002）