基于压缩传感的全息图压缩研究

李 科，李 军

(华南师范大学物理与电信工程学院，广东广州510006)

图像以其形象、生动的视觉信号表达及其信息量大的特点，一直以来都是人类获取和表达信息的重要手段之一．全息图利用“干涉记录，衍射再现”的原理，记录了物光的相位信息，其再现图像具有显著的视觉差，可以看到逼真的三维图像，对于三维成像技术的发展起着重要的作用．然而全息图数据量庞大，占用了大量存储空间和通信带宽，因此，数字全息图的压缩一直是全息技术发展中的研究热点．对于全息图压缩目前的研究思路主要集中在图像压缩前降噪和直接进行全息数据压缩上［1-2］．压缩传感(Compressive Sensing)理论［3-8］指出只要信号是稀疏的或在某个变换域是稀疏的，就可以用一个与变换基不相关的测量矩阵将变换所得到的高维信号投影到一个低维空间上，投影所得到的测量值含有足够的信息来重建信号．这个理论很快产生了可压缩成像、医学成像、地球物理数据分析、高光谱成像和可压缩雷达成像等新的研究应用．这种技术也运用到全息图的压缩表示及重建中［9-10］．本文分析了压缩传感技术对于全息图这一类包含有物体振幅和相位信息的信号进行压缩的可行性，并研究了稀疏域及重构算法对于全息图压缩的影响．

1 压缩传感原理

传统信号的获取和处理过程主要包括采样、压缩、传输和解压缩等4个部分，其采样过程必须满足奈奎斯特采样定理，即采样频率不得低于模拟信号最高频率的两倍．该方法低效，将造成巨大的浪费．采集得到的大量数据在压缩后绝大部分都将丢弃，并且随着带宽的增大，采样速率也越来越高，对硬件造成巨大的压力．近年来国际上出现的压缩传感理论为该问题提供了新的解决方案［3-5，8］．CANDÉS［3］从数学上证明了可以从部分傅里叶变换系数精确重构原始信号，为压缩传感奠定了理论基础．相对于传统方法，压缩传感理论将采样和压缩2个部分合并进行，首先采集信号的非自适应线性投影(测量值)，通过这个过程完成了采样同时获得信号的压缩表示(测量值)，然后根据这些测量值由相应重构算法重构原始信号，这部分相当于传统方法中的解压缩过程．压缩传感理论的实现必须具备以下2个条件:稀疏性和非相干性，前者是针对信号本身，后者则是对于测量矩阵．压缩传感理论主要包括信号的稀疏表示、测量矩阵和重构算法等3个方面［6］．

1．1 稀疏性

如果一个信号中只有少数元素是非零的，则该信号是稀疏的．通常时域内的自然信号都是非稀疏的，但在某些变换域可能是稀疏的．根据调和分析理论，一个长度为N的一维信号f，可以表示成一组标准正交基的线性组合

其中 Ψ=［ψ1ψ2…ψN］，ψi为列向量，N ×1 的列向量θ为其加权系数且θi=ψTix．如果θ中只有很少的大系数，则信号f是可压缩的．如果θ中只有K个非零元素，则称系数向量θ为K稀疏向量．在实际运用中，CANDÉS和TAO［8］指出只要变换系数 θ 的值从大到小呈幂次衰减的话，即

这个信号看作是K稀疏信号，可利用压缩传感理论得到恢复，并且其重构误差满足:

其中Cr为比例常数，p表示衰减的速度，0＜p＜1，p越小衰减速度越快，r=1/p-1/2．因此，对于信号，寻找合适的稀疏表达是压缩传感理论的首要任务，信号稀疏的效果直接影响信号重构的时间和效果．对于图像信号，常用的稀疏域有傅里叶域和小波域．

1．2 测量矩阵

把信号f变换到某个变换域得到变换系数的K稀疏表示后，只需找出其K个最大的变换系数就可以通过逆变换重构信号f．压缩传感理论对于信号的采集并不是直接获得K个最大的变换系数θ，而是通过把变换系数θ投影到M×K(K＜M≪N)测量矩阵Φ上，得到M个测量值y，即

1．3 重构算法

信号重构算法是压缩传感理论的核心，是指由M次测量向量y重构长度为N的稀疏信号f的过程．信号的重构过程可以通过求解最小L0范数问题加以解决，即:

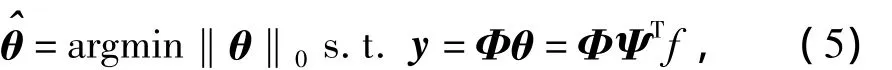
其中‖θ‖0即向量θ非零元素的个数．但是最小L0范数问题是一个NP-hard问题，无法求解．鉴于此，研究人员提出了一系列解决的算法，主要可归入以下3类:以OMP算法、分段OMP算法(StOMP)及正则化OMP算法(ROMP)为代表的贪婪追踪法;以梯度投影法、内点法、BP算法等为代表的凸松弛算法和要求信号采样支持分组测试快速重建的组合算法．在这些算法中具有代表性的算法是基追踪(BP)算法［13］和正交匹配追踪(OMP)算法［14］．

2 基于压缩传感技术的全息图压缩研究

2．1 全息图稀疏域研究

根据前述压缩传感理论，图像必须是稀疏的，而且其稀疏程度直接影响信号的重构时间和效果．所以寻找合适的稀疏基尽可能地稀疏表示信号是压缩传感的首要任务．本文使用2种常见的稀疏域来稀疏表示图像——傅里叶域和小波域．一幅大小为M×N的图像的离散傅里叶变换表示如下:

其中F(u，v)的值为傅里叶变换系数．通过傅里叶变换把图像分解为不同频率复正弦函数的叠加，其中少量基函数的系数即变换系数远远大于其他的系数，以此达到图像稀疏的目的．在图像采集的时候直接获取变换系数然后通过反变换复原图像．

与傅里叶变换不同，小波变换基于一些小型波，具有变化的频率和有限的持续时间．给定一个基函数ψ(t)，令 ，若 a，b 不断变化，则可得到一组函数ψa，b(t)．对于平方可积信号x(t)，其小波变换定义为:

文中选用sym8小波函数作为离散小波分析的基函数．针对2种变换域的稀疏化效果，本文做了如下研究:分别用自然图像和全息图像进行傅里叶变换和小波变换，然后各自使用其10%和5%最大系数进行重构，并计算峰值信噪比(表1)．从表中可以看出，在同等条件下，自然图像使用小波系数重构的峰值信噪比高于傅里叶系数，而全息图像则相反．这表明由于全息图自身的特点，其变换域的选择与自然图像有所区别．在实验研究中，本文将用小波基和正弦基这2种不同的基函数分别对图像进行稀疏化处理，然后使用同一种重构算法在相同测量值的情况下比较重构图像的效果，以此选取全息图压缩的稀疏域．

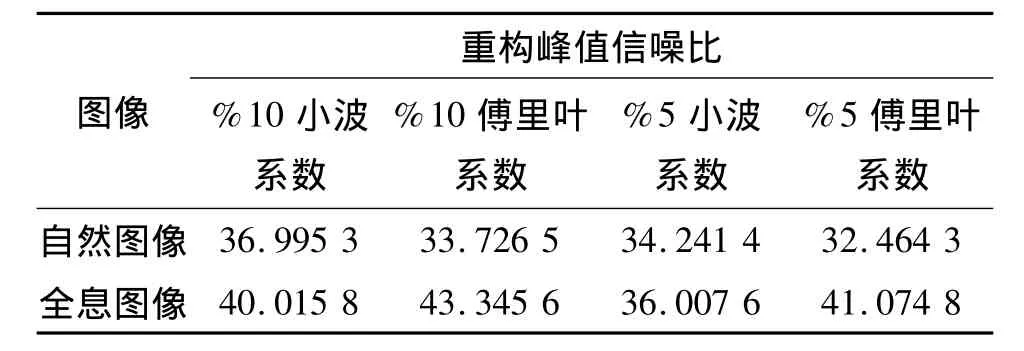
表1 全息图与自然图像不同变换域重构峰值信噪比Table 1 The PSNR of hologram and natural image reconstruction in different transform domains

2．2 重构算法比较

在获取测量值后，不同的重构算法在重构时间和重构效果上都有较大的差别．文中选取基追踪算法(BP)和正交匹配追踪算法(OMP)这2种经典重构算法，研究其对全息图重构的效果．对求解方程(4)这个欠定方程组，这2种算法采取了不同的思路．

基追踪算法由Donoho提出，其核心思想是以方程(4)为约束条件求最小L1范数的过程，即

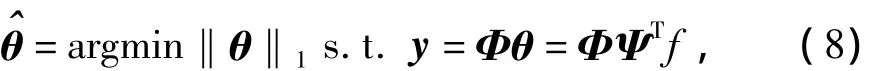
其中‖θ‖1即θ的L1范数表示θ中非零元素绝对值之和．对于二维图像信号，考虑到大部分图像梯度是稀疏的，CANDÉS等［3］提出了更适合图像重构的最小全变分法(minimization of total variation，以下简称TV)，其本质和最小L1范数法相同，只是把求解L1范数的过程变成求解最小梯度值的过程，即

其中，是图像离散梯度值之和．最小全变分法也属于基追踪算法，是专门针对图像信号的重构算法．问题(9)的求解可转换为二阶锥规划问题．

OMP算法则是一种迭代贪婪算法，通过全局最优化在正交方向上寻找非零系数，其基本思想在每一次的迭代过程中，从过完备原子库里(即测量矩阵Φ)选择与信号最匹配的原子来构建稀疏逼近，并求出信号表示残差，然后继续选择与信号残差最为匹配的原子，经过一定次数的迭代，信号可以由一些原子线性表示．

现有的研究结果表明，对于自然图像OMP算法比TV算法更快，但是精确重构的理论保证比TV算法弱，鲁棒性较差．而这2种算法对于全息图重构的影响，实验将通过在相同的稀疏域且相同数量的测量值条件下使用这2种算法对全息图进行重构，分析运算时间以及重构和全息再现效果．

3 全息图压缩实验与分析

在基于压缩传感的全息图压缩实验中，使用Mach-Zehder干涉仪获取一幅1 024*1 024大小的“N”字母全息图，其中波长为632．8 nm，记录距离95 cm，压缩重构采用 PC平台，硬件为酷睿I7 2．6 GHz、4 G 内存，软件为 Windows 7、Matlab8．0版本．分别利用小波域和傅里叶域对全息图进行稀疏表示后，使用OMP算法在相同测量值条件下重构的效果比较．图1的4幅全息图中(A)为全息图原图，(B)和(C)是在测量值个数为图像总像素的10%条件下重构的图像，其中(B)使用傅里叶域重构，(C)使用小波域稀疏后的全息图重构的效果．从(B)、(C)图可以看出使用傅里叶域稀疏的效果要明显好于小波域稀疏的效果．图2是4幅全息再现图，分别对应图1中的4幅全息图，文中使用Fresnel重建方法进行全息图再现．从图2(B)、(C)的再现效果也可以明显看出傅里叶域稀疏的效果明显好于小波域稀疏的效果．在进一步实验中也表明使用小波域时测量值个数少于总像素的7%时将无法重构图像，而在傅里叶域稀疏下仅利用1．5%的测量值还可以重构图像，如图1(D)及其再现效果(图2(D))．实验结果也表明，全息图与自然图像有较大的区别，通常自然图像使用小波域稀疏的效果要好于傅里叶域稀疏的效果，JPEG2000压缩算法的出现也证明了这一点，但是对于由干涉条纹形成的全息图像，使用平滑的正弦波作为基函数要比不规则的小波更好．

图1 使用不同稀疏域的全息图重构效果Figure 1 Hologram reconstruction using different sparse domains

图2 对应图1中4幅全息图的Fresnel再现效果Figure 2 The corresponding Fresnel holography reconstruction of four holograms in figure 1

图3是在相同测量值个数条件下OMP算法和TV算法的重构效果，使用的稀疏域都是傅里叶变换域．其中，图3(A)、(B)分别是使用OMP算法和TV算法的全息图重构效果，测量值个数为总像素的10%．从这2幅图可以看出，全息图重构及再现的效果没有太大区别．当测量值个数减少到总像素的3%时，OMP算法和TV算法重构的结果分别如图3(C)和(D)所示，从图4对应的再现效果可以看出，在如此少的测量值下还能再现出图像．而从图4(C)、(D)2幅放大后的再现图也可以看出，当测量值个数较少时，使用OMP算法重构的图4(C)字母“N”有信息丢失的情况，而图4(D)还是相对完整(矩形白圈标注部分)，TV算法的效果要稍微优于OMP算法．但是，从计算时间来看，OMP算法要比TV算法快一个数量级．考虑计算成本的情况下贪婪追踪算法更有优势，一定条件下，OMP算法要比BP算法更快，对高度稀疏的信号尤为有效，而且OMP算法在程序上更容易实现．

图3 使用不同重构算法的全息图重构效果Figure 3 Hologram reconstruction using different algorithms

图4 对应图3中4幅全息图的再现效果Figure 4 The corresponding holography reconstruction of four holograms in figure 3

结果表明，这2种算法在全息图的重构上得出的结论与自然图像一致，但是在稀疏域上则有所区别，从全息图自身干涉条纹的特点出发，使用傅里叶域能得到更好的稀疏化效果．

4 结论与展望

本文首次提出将压缩传感技术运用到全息图的压缩中，研究并分析了不同稀疏域和重构算法对于全息图压缩的影响．实验证明压缩传感技术对于全息图的压缩是可行的，并且在傅里叶域稀疏下利用OMP算法对全息图进行压缩重构可以达到很高压缩率和很快的重构速度．在后续工作中如针对稀疏表示的问题还可考虑冗余字典上的稀疏分解理论，进一步减少测量值提高重构效果．此外，对重构算法进行优化，减少其计算复杂度也是后续工作中值得研究的问题．

［1］GARCIA-SUCERQUIA J，RAMÍREZ JH，CASTANEDA R．Incoherent recovering of the spatial resolution in digital holography［J］．Optics Communications，2006，260:62-67．

［2］DARAKISE，NAUGHTON T J，SORAGHAN JJ．Compression defects in different reconstructions from phaseshifting digital holographic data［J］．Applied Optics，2007，46:4579-4586．

［3］CANDÉS E，ROMBERG J，TAO T．Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information［J］．IEEE Transactions on Information Theory，2006，52(2):489-509．

［4］DONOHO D L．Compressed sensing［J］．IEEE Transactions on Information Theory，2006，52(4):1289-1306．

［5］CANDÉSE．Compressive sampling［C］∥IEEE Proceedings of International Congress of Mathematicians．Zürich，Switzerland，2006:1433-1452．

［6］BARANIUK R．Compressive sensing［J］．IEEE Signal Processing Magazine，2007，24(4):118-121．

［7］CANDÉS E，ROMBERG J．Sparsity and incoherence in compressive sampling［J］．Inverse Problems，2007，23(3):969-985．

［8］CANDÉS E，TAO T．Near optimal signal recovery from random projections:Universal encoding strategies?［J］．IEEE Transactions on Information Theory，2006，52(12):5406-5425．

［9］MARIM Marcio M，ATLAN Michael，ANGELINI Elsa，et al．Compressed sensing with off-axis frequencyshifting holography［J］．Optics Letters，2010，35(6):871-873．

［10］BRADY D J．Compressive holography［J］．Opt Express，2009，17(15):13040-13049．

［11］CANDÉS E，TAO T．Decoding by linear programming［J］．IEEE Transactions on Information Theory，2005，51(12):4203-4215．

［12］CANDÉSE，ROMBERG J，TAO T．Stable signal recovery from incomplete and inaccurate measurement［J］．Communications on Pure and Applied Mathematics，2006，59(8):1207-1223．

［13］CHEN S B，DONOHO D L，SAUNDER M A．Atomic decomposition by basis pursuit［J］．SIAM Journal on Scientific Computing，1998，20(1):33-61．

［14］TROPP J，GILBERT A．Signal recovery from random measurements via orthogonal matching pursuit［J］．Transactions on Information Theory，2007，53(12):4655-4666．