丝杠螺母副轴向窜动误差分析及测量系统设计

姚雪峰， 于海利， 冯树龙， 齐向东

（中国科学院长春光学精密机械与物理研究所，吉林 长春 130033）

0 引 言

随着现代仪器仪表工业以及装备制造业的飞速发展，对高精度传动部件的设计、制造和检测要求越来越高。现阶段大规模使用的、用来传递运动的运动副主要有丝杠螺母副、齿轮副以及蜗轮蜗杆副等几种形式[1－7]。其中，丝杠因其能将旋转运动转换为直线运动和具有行程大及良好的机械传动特性而广泛地应用在各种工业装备、精密仪器、精密数控机床领域里，在得到了广泛推广的同时也促进了相关行业的发展和壮大，发挥了重要的作用和价值。

丝杠传动最重要的技术指标就是螺母的定位精度。由于丝杠本体和与之配套的螺母在加工过程中都会不可避免地产生螺距误差，因此，在运转时螺母的移动位移与丝杠的转角之间并不能严格的成线性比例关系，这会严重影响系统的精度和性能，尤其是在开环控制系统里。因此，如何提高螺母的定位精度成为广大工程技术人员面临的一个重要课题。

根据以往经验，一般认为丝杠的传动精度主要由丝杠以及螺母加工时产生的螺距误差以及丝杠和螺母的螺距尺寸不匹配引起的。过去人们往往试图通过提高丝杠以及螺母的机械加工精度来改善丝杠的传动精度。但在工程实践中发现，当丝杠螺母的机械加工精度到达一定水平后，继续提高加工精度并不能同比例的提高丝杠传动精度，特别是在亚微米这一精度范围内。因此，通过分析，文中提出了影响丝杠传动精度的另外一种误差，即丝杠轴向窜动误差，并进行了相关的研究。

1 丝杠轴向窜动误差产生原因

目前比较常见的丝杠安装方式示意图如图1所示。

由如图1可以看出，它主要由丝杠、螺母、钢球、两个V形轴承、封闭弹簧、套筒以及左右两个限位块组成。这种安装方式的最大优点是右端的限位块在左端滑套处封闭弹簧的作用下可以限制丝杠在轴向方向的位移。与使用滚动轴承的安装方式相比，由于具有结构简单、可靠性高的特点，而且还能消除一定的轴向间隙，因此，此方法广泛地应用在精密丝杠检测仪器以及精密定位装置等场合。

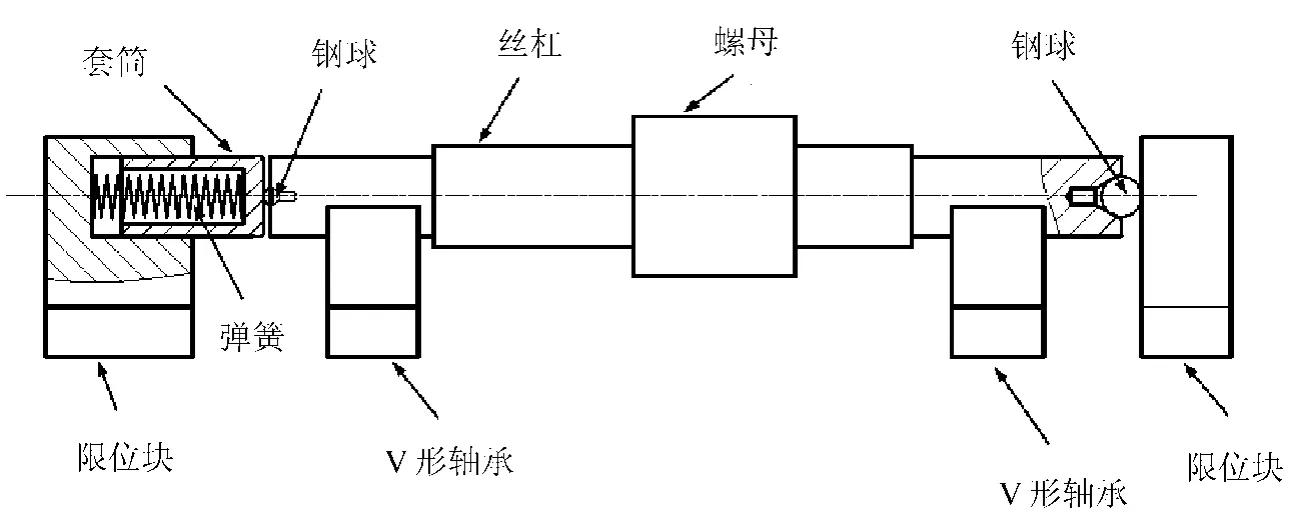
图1 目前的丝杠安装方式

虽然上述安装方式对丝杠轴向间隙有一定的消除作用，但丝杠的轴向窜动误差却无法消除。丝杠产生轴向窜动误差，原理如图2所示。

图2 轴窜误差原理图

从如图2可以看出，由于制造和装调过程中存在误差，丝杠固定端钢球球心与丝杠回转轴线有一个偏移量Δ；固定端限位块的限位面与丝杠回转轴线的法平面不重合，会有一个夹角θ。根据几何关系，在忽略钢球尺寸效应的影响下，当丝杠回转一周时，固定端钢球会在限位面上形成一个长轴长度为2Δ／cosθ，短轴长度为2Δ的椭圆形轨迹。当钢球分别处于椭圆的两个长轴顶点位置时，钢球中心在丝杠轴向方向上产生一个最大的窜动，其幅值大小为2Δ·tanθ。该窜动会给正常参与传动的螺母带来一个额外的位移，从而影响了螺母的定位精度。由于Δ，θ的确切大小无法通过测量的方式直接获得，因此，也无法通过计算的方法得到轴向窜动的准确数值。

2 丝杠轴向窜动误差测量原理

2.1 丝杠轴向窜动误差测量方法设计

为了准确得到丝杠轴向窜动的规律，并且验证理论分析结果的正确性和可靠性，文中搭建了一套丝杠轴向窜动测量系统，丝杠轴向窜动测量系统光路图如图3所示。

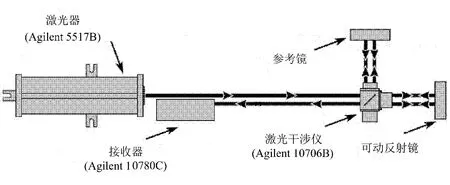
图3 测量系统光路图

从图3可以看出，测量系统的光学元件选择的都是美国惠普安捷伦公司产品，其中激光器型号是Agilent 5517B，参考频率为1.9～2.4MHz；接收器型号是Agilent 10780C；激光干涉仪的型号为Agilent 10706B，其分辨率为0.3nm。图中可动反射镜通过方位可调的转接装置和被测丝杠端部安装在一起，并且已经采用自准直法将可动反射镜的镜面与丝杠回转轴线调成了垂直状态。

在可动反射镜与丝杠回转轴线垂直的前提下转动丝杠，可动反射镜会与丝杠沿轴向同步窜动而参考镜固定不动。激光干涉仪前端的Agilent 5517B氦氖激光器上加有一个强度约为0.03特斯拉的轴向磁场。由于塞曼分裂效应和频率牵引效应，激光器产生fA和fB两个不同频率的左旋和右旋圆偏振光。经1／4波片后成为两个互相垂直的线偏振光，入射到Agilent 10706B激光干涉仪上。Agilent 10706B激光干涉仪内部光路示意图如图4所示。

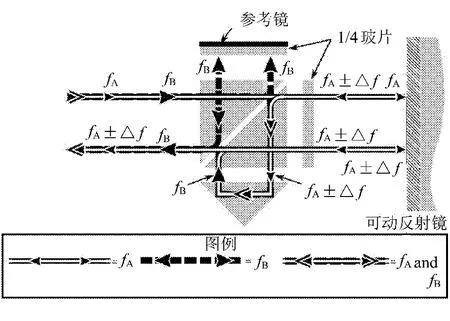
图4 Agilent 10706B激光干涉仪内部光路图

从图4可以看出，光束经内置偏振分光镜透射和反射后分为两路：一路成为仅含有fA频率的光束（透射光束）；另一路成为仅含有fB频率的光束（反射光束）。

当可动反射镜沿丝杠轴向移动时，含有fA频率的光束经可动反射镜两次反射、两次穿过1／4玻片后成为含有频率fA±2Δf的光束（Δf是可动反射镜移动时因多普勒效应产生的附加频率，正负号表示移动方向）。这路光束和由参考镜反射回来仅含有fB频率的光束经偏振分光镜后会合成为频率（fA±2Δf）－fB的测量光束。测量光束和上述参考光束经各自的光电转换元件、放大器、整形器后进入减法器相减，输出成为仅含有±2Δf的电脉冲信号。

经可逆计数器计数后，由数据采集装置进行当量换算后，即可得出可动反射镜相对于参考镜的位移量，即丝杠转动过程中的轴向窜动量。

2.2 装调误差分析

测量过程会存在以下几种误差：

1）测量装置误差，例如制造误差、安装调试误差等；

2）测量方法误差，即由于测量方法不完善、测量依据的理论不严谨产生的误差；

3）其它随机误差，包括测量过程中温度的变化、空气扰动、地面的微震、机构间隙以及运转过程中摩擦力的变化[8－16]等。

由于采用的测量方法比较成熟、测量仪器精度较高等原因，文中只侧重分析装调带来的误差。不垂直度误差示意图如图5所示。

图5 不垂直度误差示意图

当激光干涉仪的入射光束和出射光束相对于丝杠回转轴线呈非中心对称分布时，在不考虑丝杠窜动的前提下，丝杠旋转一周的过程中，激光干涉仪的光程会发生变化。由图4可知，当可动反射镜分别位于位置1和位置2时，光程变化最大。已知条件为激光干涉仪两条光束间距离为12.7mm，设光束中轴线与丝杠回转轴线偏离距离为d；可动反射镜与丝杠回转轴线法平面的夹角为α。则通过几何关系，可以推导出光程变化量M的表达式：

将d，α代入到CD，AB中，得到M 的最终表达式：

根据实验的装调条件和人员的技术水平，可以确定离轴量d小于0.2mm，α小于3″，代入到M的表达式中，得到了光程变化量M的最大值，即：

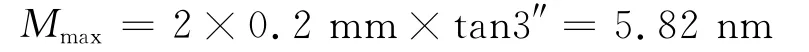
由此可见，纳米级的装调误差不会对测量结果有特别显著的影响。

3 测量实验与结果

环境对测量结果至关重要，因此，选择在±0.5℃恒温以及气浮隔振条件下，对丝杠轴向窜动进行了实验测试，如图6所示。

图6 测量系统实物图

测量系统由被测丝杠、编码器、端部钢球、两个V形轴承、推力轴承、弹簧、套筒、左右两个限位块、端面转接板、镜座、调整螺钉、拉簧、可动反射镜、参考镜、激光器、双频激光干涉仪、接收器以及数据采集装置组成。

整个测量过程由以下两个步骤完成：

1）可动反射镜端面调整示意图如图7所示。

图7 可动反射镜端面调整示意图

从图7可以看出，可动反射镜与镜座粘结在一起，镜座通过3根拉伸弹簧封闭到端面转接板上。驱动被测丝杠，采用自准直法调整支撑镜座的三根螺钉，使可动反射镜的镜面与丝杠回转轴线垂直，当平行光管数显装置在“X”，“Y”两个方向上读数变化均小于±3″时，满足精度要求，然后停止调整工作；

2）摆放各光学元器件，调整光路，使可动反射镜和参考镜反射回来的光束通过激光干涉仪后汇集到接收器上，接收器与N1231B数据采集板卡通讯后将数据传输到工控机中，得到丝杠相对参考镜的位移，即丝杠的轴向窜动量。将该位移量作为纵坐标，与之对应的编码器记录下的丝杠转角信号作为横坐标便可绘出丝杠轴向窜动误差特性曲线。最后，得到的正反向测量结果分别如图8和图9所示。

图8 正向测试结果曲线

图9 反向测试结果曲线

从图中可以看出，丝杠正转、反转测量结果趋于一致，但幅值略有不同。随着丝杠的转动，丝杠的轴向窜动也随之作周期性变化，并且变化的周期和丝杠的转动周期相吻合。轴窜的变化幅度最大为90nm；小周期内曲线并不能完全对称，经分析是钢球限位面面形不平整引起的变化；轴窜曲线波峰波谷处有波动的小毛刺，表明丝杠处于该位置时，轴向窜动比较剧烈，且变向频繁。

4 结 语

文中根据现代科学技术的要求，为了掌握丝杠的轴向窜动规律，从而实现较高的螺母定位精度，提出了一种丝杠轴向窜动的非接触测量方法。在介绍了测量系统的结构和工作原理后进行了误差分析，最后给出了测试结果。实验结果表明，丝杠的轴向窜动呈周期性变化，符合之前的理论推导；其变化幅度在90nm左右，足以影响到亚微米级的定位精度。由于测量系统采用的是激光干涉仪非接触式测量，具有精度高、可靠性好的特点，而且还不需要占用较大的空间，因此，文中设计的测量系统可以广泛地应用在对精度要求比较高，并且空间狭小、难以直接测量的场合。

[1]张策，陈树昌，孟彩芳.机械原理与机械设计[M].北京：机械工业出版社，2004.

[2]刘更，马尚君，佟瑞庭，等.行星滚柱丝杠副的新发展及关键技术[J].机械传动，2012，36（5）：103－108.

[3]毛英泰.误差理论与精度分析[M].北京：国防工业出版社，1982.

[4]牟世刚，冯显英.高速滚珠丝杠副动态特性分析[J].湖南大学学报：自然科学版，2011，38（12）：25－29.

[5]费业泰.误差理论与数据处理[M].北京：机械工业出版社，2010.

[6]林桂霞.螺杆轴向窜动误差分析[J].机械传动，2011，35（4）：61－62.

[7]丁梅，冯虎田.滚珠丝杠激光动态测量系统设计与实现[J].制造技术与机床，2011，12：37－41.

[8]刘栋，梅雪松，冯斌，等.基于Symlets小波滤波的滚珠丝杠伺服进给系统频响特性辨识[J].机械工程学报，2011，47（13）：153－159.

[9]黄琦，娄志峰，马勇，等.多齿分度盘动态分度误差分析[J].振动与冲击，2012，31（9）：172－175.

[10]葛海燕，洪荣晶，袁鸿.安装角偏差引起的成形磨齿齿形误差分析[J].机械设计与制造，2012（5）：202－204.

[11]郭夏锐，王春雨，廖志波，等.高精度透射式空间光学系统装调误差分析与动态控制[J].红外与激光工程，2012，41（4）：947－951.

[12]邓乾旺，文文.基于拉丁超立方抽样的薄板装配误差分析[J].中国机械工程，2012，23（8）：947－951.

[13]姚佳.常用高精度测量仪测量圆度误差分析[J].光学仪器，2012，34（2）：5－10.

[14]骆永洁，杨甬英，田超，等.非球面部分补偿检测系统的误差分析与处理[J].浙江大学学报：工学版，2012，46（4）：636－642，733.

[15]马宏，王金波.仪器精度理论[M].北京：北京航空航天大学出版社，2009.

[16]黄瑞宁，楼云江.微细线切割电极丝形位误差分析[J].哈尔滨工业大学学报，2012，44（3）：69－74.