双肢剪力墙内力的计算方法及荷载与抗力的统计特征探究

艾进贵

（宁夏工业设计院有限责任公司 宁夏 银川 750001）

0 引言

剪力墙结构是指纵横向主要承重构件全部为结构墙的结构。当墙体处于建筑物中合适的位置时，他们能形成一种有效抵抗水平作用的结构体系，同时，又能起到对空间的分割作用。 近年来，由于住宅需求的增加和用于建造住宅的土地供应紧张，高层住宅的建造成为众多开发商的首选，推动了剪力墙结构的广泛应用。

1 内力的计算方法

1.1 地震作用

双肢剪力墙是多自由度超静定平面结构。对于多自由度弹性体系的水平地震作用一般采用底部剪力法和振型分解法求得。对于高度不超过40m、 以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构可采用底部剪力法。 但双肢剪力墙的变形以弯曲变形为主，根据《高层建筑混凝土结构技术规程》JGJ3-2002 中3.3.4 的规定：高层建筑结构宜采用振型分解反应谱法。 所以在本文中计算地震作用时采用振型分解法。

《建筑抗震设计规范》GB50011-2010 中规定， 采用振型分解反应谱法时，不进行扭转耦联计算的结构，按下列规定计算其地震作用和作用效应：

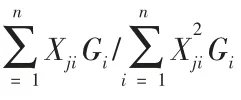
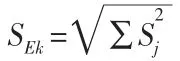
1.2 双肢剪力墙的内力计算

文献[1]中总结了双肢剪力墙内力计算的方法。

1.3 内力的最不利组合

剪力墙为偏心受力构件， 取每层的底部和顶部作为控制截面；连梁主要承受水平荷载产生的内力，一般取梁端截面为控制截面。 根据《高层建筑混凝土结构技术规程》JGJ3-2002 中5.6 节中的规定， 高层双肢剪力墙应以下列方法组合：

（1）无地震作用效应组合时，荷载效应组合的设计值为S=γGSGk+ψQγQSQk+ψWγWSWk。

（2）有地震作用效应组合时，荷载效应和地震作用效应组合的设计值为S=γGSGE+γEhkSEhk+γRvSRvk+ψWγWSWk。

论文中涉及到的内力组合有以下三种，由此三种组合中可得到最不利内力组合：

（1）无地震作用活荷载中楼面活荷载起主导作用时S=1.2SGk+1.0×1.4×SQk。

（2）无地震作用永久荷载起主导作用时S=1.35SGk+0.7×1.4×SQk。

（3）有地震作用时S=1.2SGE+1.3SEhk=1.2×（SGk+0.5SQk）+1.3SEhk。

2 荷载的统计特征

对于结构荷载，国内外采用两种概率模型。 对于恒载这样与时间无关的永久荷载，采用随机变量模型；对于楼面活荷载、风荷载、雪荷载这样与时间参数有关的可变荷载，则采用随机过程模型。 我国目前将各种可变荷载的模型统一取平稳二项随机模型。

根据办公楼、住宅楼面活荷载的特点，可将活荷载分为持久性楼面活荷载和临时性楼面活荷载。持久性活荷载是指在设计基准期内任何时刻都存在，出现概率p=1 的活荷载；临时性活荷载是指在设计基准期内频繁出现且持续时间较短的活荷载。 通过统计分析，持久性活荷载任意时点服从极值Ⅰ型分布。临时性活荷载，可认定在10 年内也服从极值Ⅰ型分布。在设计基准使用期内，按《建筑结构可靠度设计统一标准》的荷载组合原则，楼面活荷载考虑以下两种组合方式：

第一种，是持久性活荷载在设计基准期内的最大值与临时性活荷载的任意时点分布值的组合，即LT1=LiT+LrS。

第二种，是持久性活荷载的任意时点分布值与临时性活荷载在设计基准期内的最大值的组合，即LT2=LiS+LrT。

以上两式中Li表示楼面持久性活荷载，Lr表示楼面临时活荷载，加足标T 表示设计基准期内的最大值，活荷载的任意时点分布加足标S。

根据目前研究的成果， 地震烈度的概率函数服从极值Ⅲ型分布。建议50 年基准期内，结构基地剪力的概率分布服从极值Ⅱ型分布。

3 抗力的统计特征

结构构件的抗力是指结构构件抵抗外加作用和变形的能力。影响结构构件抗力不定性的因素主要有三方面：

3.1 结构构件材料性能的不确定性

材料性能是指材料的强度、刚度、弹性模量、屈服比等物理力学性能。 由于材料质量、加工工艺、外界环境、尺寸等因素引起的结构构件中材料性能的变异性，称之为结构构件的材料性能不确定性。 在实际的结构工程中，对于构件的材料性能，要考虑到材料实际性能与标准试件材料的差异。

3.2 结构构件几何参数的不定性

结构构件的几何参数是指构件的截面几何特征，其不确定性产生的原因可以归结为两类：（1）初始偏差（放线、制造、生产等）引起的不确定性，与时间变化无关；（2）由荷载作用、物理化学等作用引起的不确定性，与时间变化有关。 所以对几何参数不确定性的考虑是必不可少的。

3.3 结构构件计算模式的不定性

结构抗力的计算公式是通过理论分析和总结以往经验的基础上不断总结得来的，其精确度有待考量，所以需要考虑在抗力计算中由基本假定的近似性公式的不精确性引起的误差。

为了简化确定抗力的统计参数，抗力的各种影响因素都可当做与时间无关的随机变量来考虑。直接统计各种结构构件的抗力仍存在困难，目前的做法是先确定各影响抗力的因素的统计特征参数，然后根据抗力与各因素之间的函数关系，运用统计参数运算方法，即误差传递公式求出结构构件抗力的统计参数。 由于结构构件抗力R 一般都是多个随机变量的函数，其概率分布往往是偏态，一般假定抗力R 服从对数正态分布，其统计参数μ 和σ 按误差传递公式求出。

4 结束语

总之，纵观近年来国内外对联肢剪力墙的大量实验研究，联肢剪力墙在洞口间连梁和墙肢底部处容易破坏。 墙肢底部破坏表现为，纵向受拉钢筋屈服，墙肢受压区混凝土压碎。 连梁的破坏形态有斜拉破坏、斜压破坏、剪切-滑移破坏以及弯剪破坏。 若能在保证墙肢不破坏的前提下，增加连梁的塑性转动能力，能使剪力墙获得较大的塑性变形能力。因此，设计具有适当强度、刚度和良好变形性能连梁的联肢剪力墙对改善结构体系的抗震性能，提高抗震能力至关重要。

［1］包世华,方鄂华.高层建筑结构设计[M].北京:清华大学出版社,1990.

［2］王刚,王琼梅.双肢剪力墙中连梁延性的研究[J].四川建筑科学研究,2007,33(6):41-44.

［3］贡金鑫,赵国藩.相关荷载效应组合及结构可靠度计算[J].工程力学,2001,18(4):1-6.

［4］史庆轩,梁兴文.高层建筑结构[M].北京:北京科学出版社,2004.

［5］余安东,叶润修.建筑结构的安全性与可靠性[M].上海:上海科学技术出版社,1986.