一种基于SFS方法的含高光表面三维重构系统*
2012-08-15王国珲马凤军
王国珲,苏 炜,马凤军
(1.西安工业大学 光电工程学院,陕西 西安 710032;2.西安利君制药有限责任公司,陕西 西安 710077)
引 言
通常,物体的三维信息获取技术有两大类:接触式测量和非接触式测量[1]。尽管接触式测量技术比较成熟,且能够获得很高精度,但存在诸如测量环境要求高、测量效率低等不足,限制了它的应用场合。从明暗恢复形状(shape from shading,SFS)方法作为一种被动非接触式测量技术,弥补了上述的不足,它仅利用单幅图像的明暗变化来重构物体表面的三维信息,技术原理相对简单、适用性强,因而已经成为计算机视觉领域的研究热点。
传统的基于SFS方法的三维重构系统常使用Lambert模型描述物体表面的反射特性,在重构含高光的表面时,会导致较大误差,这是因为含高光表面既含有漫反射成分又含有镜面反射成分[2]。
针对含高光表面三维形状重构的需求,设计一种新的基于SFS方法的三维重构系统。文中分析重构系统的组成,详细介绍了系统软件的设计过程,同时为了减少重构误差,使用Ward反射模型表述含高光表面的反射特性,并通过实验对重构系统进行了验证。
1 基于SFS方法的含高光表面三维重构系统
1.1 三维重构系统组成

图1 基于SFS方法的含高光表面三维重构系统Fig.1 SFS-based 3Drecovery system for surfaces with highlight
基于SFS方法的含高光表面三维重构系统由CCD相机、光学镜头、点光源、计算机以及被重构物体构成。三维重构系统的示意图如图1所示。
图1中,含高光表面物体表面被点光源照亮后,向外辐射能量;光学镜头收集物体表面反射的光线,聚焦于CCD相机的成像平面上,此时图像的辐照度代表了物体表面的辐射亮度;CCD相机获取的图像经千兆网口送入上位计算机,上位机根据图像信息得到图像辐照度,由系统软件计算含高光表面的三维形状,进而重构出物体表面。根据系统的结构,可以测量得到点光源的方向向量L,CCD相机的方向向量V。
1.2 含高光物体表面的图像辐照度
为了获取含高光物体表面的辐照度,建立以测量基面为中心的三维笛卡尔坐标系o-xyz:设定测量基面的中心对称点为坐标系的原点o;调整CCD相机的位置,使得坐标系的z轴与CCD相机光轴重合,坐标系的x轴与CCD相机像元水平排列方向一致,坐标系的y轴与CCD相机像元垂直排列方向一致。
在CCD相机遵循正交投影条件下,物体表面某一点(x,y,z(x,y))在成像表面的投影为(u,v),即:

式(1)中,zf为CCD相机成像平面在z轴的位置,Ω为CCD相机获得的图像区域。
由微分几何曲面理论知,物体表面某点(x,y,z(x,y))的方向向量n可以表示为[3]

由于需要对含高光表面进行三维形状重构,系统使用 Ward反射模型[4-5]描述含高光表面的反射特性。Ward模型使用Gauss分布函数描述了含高光表面反射中的镜面成分,利用 Ward模型可以计算物体表面的辐射亮度:
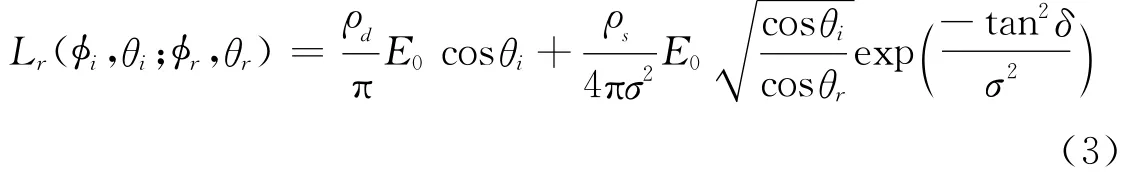
式(3)中,ρd为含高光表面漫反射率;ρs为含高光表面镜面反射率;E0为点光源的发光强度;σ为Gauss分布函数的标准差,代表了物体表面的粗糙程度。其余参数的几何关系参见如图2所示的物体表面某一点的局部坐标系nx′y′,图中φi,θi和φr,θr分别为光源方向向量L和CCD相机方向向量V的方位角和天顶角;δ为物体表面法向量n与h之间的夹角,其中h为光源与CCD相机的夹角平分线的方向向量。

图2 物体表面反射几何关系Fig.2 Reflection geometry relationships on the object surface
系统在进行结构设计时,将点光源方向设置为平行于CCD相机的光轴,于是可以得到点光源的方向向量为

且有θi=θr,φr=φi。此时物体表面的辐射亮度式(3)变为

由于θi为n与L之间的夹角,故有

将式(6)代入式(5),得到含高光物体表面的图像辐照度

式(7)中,η为一个常数,与点光源的发光强度E0、CCD相机的成像参数以及光学镜头的参数(如镜头的直径、焦距)等有关,系统可以通过标定来获得η的值。
2 系统软件设计
系统软件设计主要包含两个方面:(1)使计算机能够驱动、控制CCD相机获取被重构物体的图像;(2)根据获取的图像信息,建立了物体表面的图像辐照度式(7),调用求解算法计算该方程,进而输出重构结果。第一部分可以通过调用CCD相机自带的驱动程序及相关实例来设计;第二部分是系统软件设计的重点,文中仅说明此部分。
系统软件的流程图如图3所示,其中图3(a)为系统软件的主程序流程图。CCD相机获取的含高光物体表面图像经千兆网口送入计算机,主程序得到图像后,计算出图像中每个像素点的辐照度,然后调用SFS方法子程序求解图像辐照度方程,因为图像辐照度方程的解即为物体表面三维形状函数z(x,y),于是可以获取含高光表面的三维形状,最后输出重构结果。
图3(b)为SFS方法子程序流程图。首先,将含高光表面图像辐照度方程转化为包含物体高度信息的H-J偏微分方程;接着为了求解该方程,一种直接的方法就是将其转化为时变问题,使用二维中心Hamilton函数[6]和不动点迭代sweeping方法[7-8]计算上述时变问题的解,进而获取含高光物体表面图像辐照度方程的解。
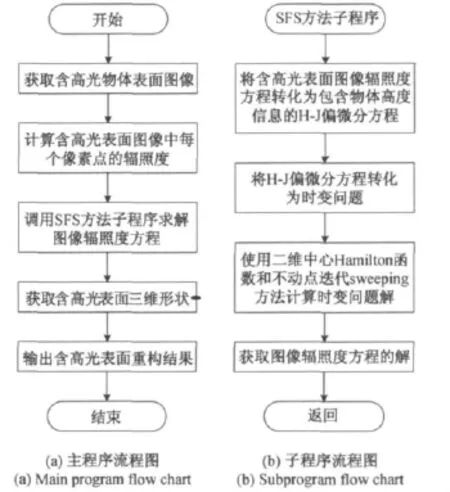
图3 含高光表面三维重构系统软件流程图Fig.3 Software flow charts for 3Drecovery system for surfaces with highlight
3 实 验
为了考察系统的性能,使用一幅已知三维形状的含高光物体表面图像进行验证,实验结果如图4所示。
图4(a)是含高光物体表面三维形状的真实高度值,图4(b)为获取的含高光物体表面图像。图4(c)是使用系统重构的三维形状,SFS方法子程序在迭代50次后收敛,系统耗时0.6s,由此可以看出该系统具有速度快、测量效率高的特点。图4(d)为图4(c)与图4(a)之间的高度误差图,为了定量评价系统的恢复结果,用高度平均绝对误差(mean absolute error,MAE)和高度均方根误差(root mean square error,RMSE)作为指标,计算MAE和RMSE分别为2.97和3.20;由图4(c)和图4(d)及上述数据可以看出,该系统的重构精度较高,能够满足性能要求。

图4 含高光表面三维重构系统实验结果Fig.4 Experimental results of 3Drecovery system for surfaces with highlight
4 结 论
设计了一种基于SFS方法的含高光表面三维重构系统,能够实现含高光表面三维形状重构的需求。首先,在正交投影条件下CCD相机获取点光源照射下的物体表面图像;其次,使用Ward反射模型描述含高光表面的反射特性,建立物体表面图像辐照度方程;然后,将该方程转化为包含物体高度信息的H-J偏微分方程;接着,将其转化为时变问题,使用二维中心Hamilton函数和不动点迭代sweeping方法求解上述时变问题,进而获取图像辐照度方程的解;最后,恢复出物体的表面形状。实验结果表明,该系统可以快速、有效地重构出含高光表面的三维形状。然而,标定系统获得η值是一个非常复杂的过程,如何实现简易标定系统将是下一步研究工作的重点。
[1]王国珲,王 建,孙 帅.SFS三维重构技术的发展现状与趋势研究[J].光学仪器,2011,33(4):90-94.
[2]王国珲,韩九强,张新曼,等.一种从混合表面的明暗变化恢复形状的新算法[J].宇航学报,2011,32(5):1124-1129.
[3]王国珲,韩九强,张新曼.一种适合漫反射表面从明暗恢复形状的快速算法[J].西安交通大学学报,2009,43(10):7-10,21.
[4]WARD G J.Measuring and modeling anisotropic reflection[J].ACM SIGGRAPH Computer Graphics,1992,26(2):265-272.
[5]AHMED A H,FARAG A A.Shape from shading for hybrid surfaces[C]∥Proceedings of the IEEE International Conference on Image Processing.Piscataway:IEEE,2007:525-528.
[6]SHU C W.High order numerical methods for time-dependent Hamilton-Jacobi equations[M]∥GOH S S,RON A,SHEN Z.Mathematics and computation in imaging science and information processing.Singapore:World Scientific Publishing,2007:47-91.
[7]ZHANG Y T,ZHAO H K,CHEN S.Fixed-point iterative sweeping methods for static Hamilton-Jacobi equations[J].Methods and Applications of Analysis,2006,13(3):299-320.
[8]ZHAO H K.A fast sweeping method for Eikonal equations[J].Mathematics of Computation,2005,74(2):603-627.
