逆向工程中的点云采样算法研究

林秀芳

（福建农林大学 金山学院，福建 福州 350002）

作为产品设计制造的一种手段，在20世纪90年代初，逆向工程技术开始引起了各国工业界的高度重视。逆向工程，又称反求工程（Reverse Engineering），是将已有产品模型或实物模型转化为工程设计模型和概念模型，再在此基础上对已有产品进行再设计和制造。逆向工程的体系结构由数据获取、数据处理、曲面建模以及基于CAD模型的再设计和产品制造组成[1]。

测量数据点云一般密度很大，所构造的三角面片模型容量过于巨大，因此存储、处理或显示都将消耗大量的时间和计算机资源。另外，用于误差评价时，点云也不能过密，否则计算量会更大，将消耗大量的时间。因此，在逆向工程中测量数据的精简是数据处理的重要工作之一，而点云采样是数据精简的一个重要方法。

激光扫描仪获取的扫描线数据排列密集，没有明显的拓扑关系，为了满足CAD建模软件的要求，应生成矩形拓扑网格形式的数据。矩形拓扑网格点应随着曲面曲率变化而变化，曲率越大部分，采样点应当越密集，曲率小的部分，采样点应当稀疏。Pahk[2]初步探讨了在模具型面上随曲率变化的采样的问题。Li[3]提出了依据曲率测度的采样网格产生方法，该方法能自组织地形成拓扑网格，但没有研究逆向工程中，在给定曲面建模逼近精度的条件下，如何选取采样点的问题。文献[4]中探讨了随曲率变化的采样布点，但没有涉及如何在给定采样精度下选取最少的采样点。文献[5]中虽然给出了一种确定合理采样点数的方法，但其就几何意义并不明确。

1 点云采样算法描述

本文先用准均匀B样条曲线对激光扫描线点云数据进行逼近拟合，然后利用曲率获得重采样点，最后对两两相邻的曲线进行采样点的匹配细分，生成网格状数据点阵作为曲面建模的型值点，以满足CAD软件建模的要求。

1.1 截面曲线上密集测量数据点的B样条曲线逼近

本文采用的准均匀B样条曲线类型可以使人们对曲线在端点的行为有更好的控制，从而提高了曲线的灵活度和逼近的精度。此外，在求解B样条曲线的控制点时本文用最小二乘逼近法，在保证精确度的同时可以提高计算效率。

下面介绍如何采用准均匀B逼近算法对截面曲线数据进行拟合[6]。 设截面曲线数据点列为 Pi，i=0，1，…，m，拟合后的B样条曲线为

其中 Nj，k（u）为 k 次 B 样条基函数（k=3），而 dj是待求的B样条控制点。

1.2 基于曲率特征的采样规划算法

基于曲率特征的采样是指在曲线曲率大的部分采样点分布应当密集，在曲率小的地方分布应当稀疏。本文采用了根据质点系平衡原理的局部插值方法来计算采样点的分布[7]。如图1所示质点系，若质点m1和m2分别位于u轴上的u1和u2处，且m1>m2，则质点系的质心u在轴上的位置uc为:

图1 质点系Fig.1 System of particles

上式可进一步写成一般的力矩平衡方程形式：

其中uc是平衡质点系的质心位置，uj是平衡质点系中各指点的空间位置，其质量为 mj，j=1，2，L。 显然如果 mj越大，质心位置uc就越接近质点位置uj。相似地，可以将这个原理用于截面曲线采样点的自适应生成。也即若将各点的曲率函数k（u）视为各质点的质量，则质心的位置将趋于曲率大的部分。

1.3 矩形拓扑网格数据点阵的生成

完成所有曲线依照曲率变化规划采样点分布后，采用曲线间采样点匹配细分方法。曲线间采样点匹配是指在相邻的两条截面曲线ci和ci+1之间，取采样点数少的曲线ci上的一个点，然后在另一曲线ci+1的采样点中寻找其对应点，对应点定义为ci+1在上所有采样点与其距离最近的点。

当ci上所有点找到对应点之后，对曲线ci进行细分。

1） 令 si，y和 si+1，y分别表示相邻曲线 ci和 ci+1上相互匹配的采样点，其中y=1，2，…m，m是ci的采样点数。首先规定这两条截面曲线ci和ci+1的首末采样点一一对应，即si，1对应于si+1，1，si，m对应于 si+1，m。

2） 假设曲线 ci+1上 si+1，y和 si+1，y+1间有未被匹配的点 pi+1，y，x，其中 x=1，2， …n，n 是 si+1，y 和 si+1，y+1间的未被匹配的点的数目。 应该按照 pi+1，y，1、pi+1，y，2…pi+1，y，n的顺序依次往下确定各个点对应于ci上的细分点，具体步骤是：为了确保在ci找到的细分点与 pi+1，y，x相对应， 就要计算出 pi+1，y，x将 si+1，y 和 si+1，y+1间的曲线分成两段曲线和弧长的 比 例 ，然 后按同样的比例在曲线ci的 si，y和si，y+1间的曲线上增加一个采样点，以此作为 pi+1，y，x的对应点。

即使相邻曲线的曲率变化差异很大，也可以实现采样点的细分，如图2所示。按上述方法处理所有曲线，可获得矩形网格数据点阵。

2 应用实例

为了验证改进算法的可靠性，即使两两扫描曲线间曲率变化差异很大，也可以实现曲线间采样点的细分，本章把自适应重采样算法应用于小熊蝴蝶结测量数据的建模。小熊蝴蝶结测量数据如图3所示。

首先用B样条曲线逼近每条截面曲线上的测量数据，以其中一条截面曲线为例，该截面线的测量点如图4所示，其相对应的逼近曲线和截面线上的采样点如图5所示。

图2 细分方法的效果图Fig.2 Effect drawing of subdivision method

图3 蝴蝶结模型测量数据Fig.3 Measurement data of bowknot modle

图4 截面线测点Fig.4 Measurement point of section line

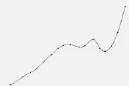
图5 截面线的B样条拟合曲线和采样Fig.5 B-Spline curve and sampling points of section line

经曲线间节点匹配、细分生成矩形拓扑网格数据如图6所示。

由采样数据在I-DEAS建立的曲面模型如图7所示。

3 结束语

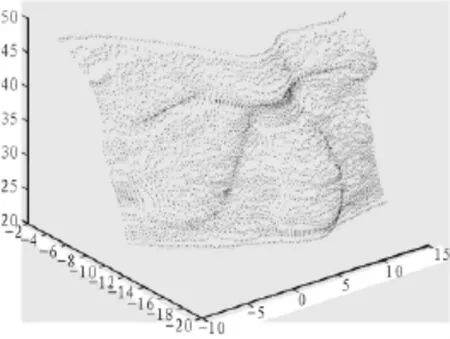
图6 匹配细分后的矩形拓扑网格数据Fig.6 Rectangular topology grid data after matching and segmentation

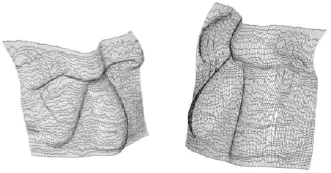
图7 网格化模型Fig.7 Griddized model

本文采样的对象是扫描线点云数据，扫描线是被测物体的截面曲线，彼此位于垂直于X或者Y轴的截面上，即平面曲线。在逼近拟合扫描线数据时用准均匀B样条曲线，提高了曲线的灵活度和逼近的精度。此外，此算法中采样点细分方法适应性强，不受两两曲线间曲率变化差异大小的影响。但由于文中所改进的自适应重采样算法只是针对扫描线点云数据，所以如何把自适应重采样算法扩展到处理散乱点云的邻域也是一个值得研究的问题。

[1]金涛，童水光.逆向工程技术[M].北京：机械工业出版社，2003.

[2]Pahk H K.Development of computer-aided inspection system with CMM for integrated mold manufacturing[J].Annals of the CIRP，1993（42）：557-560.

[3]Li S Z.Adaptive sampling and mesh generation[J].Computer Aided Design，1995，27（3）：235-240.

[4]来新民，黄田，林忠钦.基于模型NURBS的散乱数据点自由曲面重构[J].计算机辅助设计与图形学学报，1999，11（5）:433-436.LAI Xin-min，HUANG Tian，LIN Zhong-qin.NURBS based approach of surface reconstruction from scattered data[J].Journal of CAD and Graphics，1999，11（5）:433-436.

[5]来新民，黄田，林忠钦.数学模型已知的自由曲面数字化自适应采样[J].计算机辅助设计与图形学学报，1999，11（4）：359-362.LAI Xin-min，HUANG Tian，LIN Zhong-qin. Known mathematical model[J].Journal of CAD and Graphics，1999，11（4）：359-362.

[6]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京：北京航天航空大学出版社，1994.

[7]刘志刚.逆向工程中线结构光视觉传感器与CMM集成测量技术研究[D].西安:西安交通大学，2000.