基于核的MMKP问题算法研究

郑晓月

（商丘师范学院 计算机与信息技术学院，河南 商丘 476000）

背包核首次应用是在解决大（无关联）背包问题上。Balas和Zemel（1980）根据实验观察到线形松弛背包问题（LKP）的解与求KP问题最优解的不同仅体现在几个元素上，他们将包含这些元素的区间作为核。由于问题求解之前无法精确标识核，他们就通过估计中心元素附近区域的大小用一个近似区间来表示核[1]。使用背包核可以在分支定界（B&B）算法中获得一个较好的下限。

这个近似核虽然使得分支定界算法效率有所提高但是核的大小却是固定的（Martello&Toth，1990）。Pisinger引入了核的动态扩展思想并把它应用到B&B算法中（Pisinger，1994），后来又用于动态规划算法（minknap）（Pisinger，1997）。Pisinger又将这些思想应用于MCKP问题并获得了有效的解决MCKP问题的动态规划算法（Pisinger，1995）。在多维背包问题中，Puchinger，Raidl和Pferschy最近提出了一种新方法用来标识核，并且将其应用于一个模拟框架和一个松弛导向变量区域搜索以获得近似方法用来解决MKP问题[2]。

鉴于核思想成功解决了很多一般背包问题，文中导出一个处理多维多选择背包问题（MMKP）的近似核，并用它精确处理这类问题。用三步连续的过程来定义核。方法是在解空间取一个基点，然后定义一个变量的排序关系。接着这个排序关系将被用来定义基点附近构成背包核的合适子空间。

1MMKP核的确定

据Balas和Zemel的定义，核是背包最优解空间和相关线性背包最优解空间中具有不同值的元素所构成集合的最小区域。精确的定义核C可以这样表述（没有临界元素的情况不算在内）：

其中，x*背包问题的最优解，N是根据它们的性价比排序后元素的集合。

不幸的是，在解决背包问题之前这样的核是没办法找到的，必须找一种方法来获得一种近似核。根据实验，可以通过

下面3步得到MMKP问题的一个近似核，具体步骤是：1）取解空间中的任意解x（有可能是不可行的），称之为基础解或者基本解。把它作为核的中心，核将围绕这个中心来定义。如果这个点临近一个最优解，就可以得到一个小型准确核。由于一个最优解可能靠近可行性区域的边界，因此并不强制要求基本解是可行的。为了简单起见，还假设这个基本解是整形，它可以是松弛问题的四舍五入解或者启发式解。

2）在变量中定义一个全序关系。令x*为最优解，并将元素 i的变化概率表示为 Pch（i）=Pr{x*i≠xi}，其中 P是问题所有情况下的变化概率。特别关注了具有下面特性的有序关系式：

其中N是变量集合，≤0是集合上的有序关系。有序关系初始位置上的变量在最优解上比在基本解上更可能取不同的值。

根据实验获得这种有序关系的方法是，首先要从统计学的观点通过几个实例对比基本解和最优解[3]，并且估计每个变量的变化概率。然后，检查各个优先函数以便找到一个适合赋予具有较高变化概率变量较高优先权的函数，最后基于优先权值定义有序关系。

3）利用这个有序关系围绕基本解定义一个子空间。做这件事有一个简单的方法，那就是取关系中第一个变量k作为核中元素，并且在基本解中固定其他变量的值。假设所有元素已经根据有序关系排序，则核可以用下式表示：

而且，子空间可以通过设置xi=x~ii∉C来定义。通过这个方法，这个有序关系可以随着核的扩展，通过的增加轻松拓展子空间。在解空间上增加约束条件可以用来定义子空间，在前面的方法中，变量固定就相当于给等式添加了约束。因此，可以假设元素已经根据有序关系排序，通过添加与基本解相关的约束来定义子空间。下面的篇幅中将会用到这种思想。

在多维多选择背包问题中，可以定义两种有序关系而不是一种，一种是针对类的，一种是针对每类中元素的。因此，可以基于这两种有序关系来确定子空间。举个例子：根据这两种有序关系对各类和类中元素都进行排序，然后首先取k1类子集和在这些类中k2元素子集，其他g-k1类子集中变量根据基本解进行设置，设置类 i（i=1，…，k1）中其他 ni-k2元素的变量为0。这也可以从另一方面看，令和 x∈{0，1}t为一个代表MMKP整数解的t维向量。这个解用另一种方式可以表示成一个g维向量s，其中Si∈Ni·si表示类i中该元素被选定。根据（4）式，这两种表达形式是一致的。

将上式看作解的整数表达式，在这个表达式中，核可以被看做一个变量的子集和一个变量所能取得的值的子集。

2MMKP问题的精确算法

这一部分主要阐述精确解决MMKP问题的B&B算法。先是谈一下算法的总体概要，接着是描述算法每一步的细节，最后分析了算法的存储复杂度。

2.1 树结构和遍历算法

不像以前核的大小固定，取而代之的是现在排列的B&B树导致核会随着遍历而增大。假设已经根据前部分定义的MMKP核对类和元素进行了排序。树就会自然基于核中定义的排序方法就像图1描述的那样排列。这棵树共有层。树的i层对应第（g-i+1）类。层的i分支对应类的元素。第i层第j条分支的扩展节点用nij来表示。图1是B&B树的结构，和元素都已基于核中定义的有序关系排序，第一组元素构成了基本解。

图1 B&B树的结构Fig.1 Structure of B&B tree

算法.基于核的B&B算法

输入.一个MMKP问题的实例。

输出.一个关于问题的准确可行性解或者声明问题的不可行性

//步骤 1：预处理

1）处理对应的LMMKP问题。令lmmkp为计算得到的解。

2）如果lmmkp是整数的或者不可行的，则终止算法。

3）使用lmmkp的双值计算关联MCKP问题。

4）处理关联LMCKP问题。令lmckp为计算得到的解。同时，将上凸线存入一个双链接列表。

//步骤 2：约束处理

1）基于约束的松紧程度对约束集合进行排序。

2）去掉负系数。

3）使用lmmkp的双值计算混合替代约束并将它添加到约束集合中。

//步骤3:核计算（根据第3部分定义的方法）

1）四舍五入lmckp获得基本解。

2）在lmckp中使用临界差别对类进行排序。

3）在lmmkp中使用检验数在每一个类中对元素进行排序。

//步骤 4：遍历

1）使用核来构造树。

2）设置当前解状态为null，设置X为null。

3）深度优先遍历树：

①对于每一个节点 ni，j：的应用。 因为有 O（ng）条线，总的i.设置 Xg-i+1=j.

ii.使用lmckp和上凸线遍历计算上限。

iii.如果X违反某一个约束条件、或者无法推导出可行性解、或者计算出的上限不如当前上限，则去除当前节点。

②无论何时遍历到树根并且X是一个比当前解更好的解则：

i.用替换当前解。

ii.更新混合替代约束。

iii.使用lmckp固定变量。

4）返回当前结果或者如果解为空则声明问题不可行。

对树采用深度优先的方式进行遍历。遍历过程中，当取ni，j的值时设 Xg-i+1=j，其中 X是当前部分解的整数表示，Xk是它的第k部分。因为核中的类是根据变化概率的减少来排序的，树末端的那些类更可能取他们基本解的值而不是别的什么值。因此，通过这种形式的遍历，能更好地确定类的值，而且这种遍历消耗很少的内存。当算法遍历到树根时，如果能找到更好的解，当前解将被替换。注意，由于基本解是可行的，并且手动将基本解的元素放在开始位置，所以算法遍历到的第一个当前解就是基本解。

下一部分添加测深实验后，当算法遍历这棵树时实际上就是在模仿核的扩展操作。算法通过基本解开始运行，如果算法无法证明这个解的最优性，它就会定义只有一个类（类1）的核并固定其他类的变量，然后算法完全枚举这个核推导出的子空间。如果用测深实验无法证实最优性，算法会用下一个最有可能的类扩展核并且当核外类的变量固定时完全枚举核的子空间，等等。很容易看出来，为了获得最优解，算法经过完全搜索核空间后扩展核仍然是根据类的大小保持着最小扩展属性[4]。由于核中元素也是经过排序的，所以算法首先检测到得元素最有可能被纳入最优解，所以很可能快速得到最优解。就像前面提到的，核的这种使用策略类似B&B算法中变量和节点选择的启发式方法。

2.2 测深实验

为了有效地修剪子树，用3步操作对一个节点做测深实验。如果该节点在这3步操作的某一步失败了，它将被测出深度。第一个实验，使用混合替代约束的扩展。令一般的0-1背包问题为：

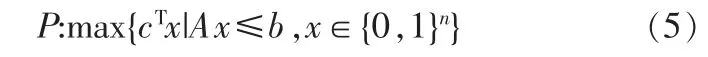
其中c是一个n维目标系数向量，A是一个非负约束系数m×n矩阵，b是一个约束的右端项m维向量。带有目标函数约束的替代约束将伴随结果出现在下面的约束公式中，称为公式（5）的混合替代约束：

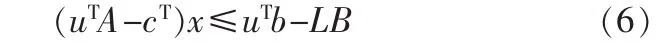
其中u是一个双乘数的m维向量，LB是问题实例的下限。这个约束可被用于变量固定和多维背包问题中嵌套逻辑消减的产生。

通过观察发现因为这个约束较紧，并且可用于固定变量，因此可以像其他约束一样对其进行扩展并有效用于测深实验。注意在混合替代约束中，简单上限被排除掉以便获得较强的约束。对于MMKP问题，GUB约束被排除掉就是这样的原因。如果任意节点都可能违反约束限制，说明约束是有效的，并且这些节点可以被测深[5]。用当前下限的值作为LB，因此这个约束的右端项将会随着遍历的进行动态变化。

第二个实验中，只是简单地检测一下一个节点能否推导出一个可行解。公式（7）帮助完成这个检测。如果下式成立则ni，j被 做 测 深 处 理 ：

公式（7）意思是，即使累加某个约束的消耗量和剩余类的最小消耗以至违犯了约束限制，仍然没有能从该节点中导出可行解。在每个节点中，保存每个约束（包括混合替代约束）消耗量的和，因此利用父节点的信息我们可以逐步计算出上面的检测结果。

最后，使用关联LMCKP问题计算一个节点的上限并与当前值相比较。如果它小于等于当前值，则当前节点将被做测深处理。由于这一步最浪费时间，所以将其放在后面。

2.3 变量固定和预处理

为了进一步缩小搜索空间范围，每当算法使用下面的公式（8）获得一个新值时就固定下变量。

其中UB（MMKP|xij=1）是MMKP的上限函数，附加约束为xij=1，LB中存放当前约束的值。UB可以在上面的fathoming实验中计算出来。但是为了加快计算速度，对关联LMCKP问题使用一个较弱的上限。

算法的预处理分成两步。第1步，从新整理约束。经过第2个fathoming实验中，检测了所有的约束，目的是找到有可能违反约束条件的节点。如果首先考虑较为严格的约束，则期待的约束检测的个数就会减少[6]，用公式（9）计算约束的严格程度：

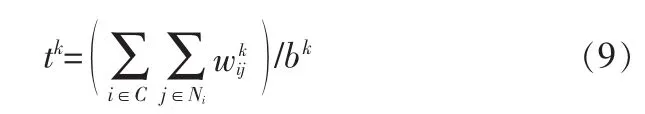
预处理第2步是，用约束式（10）替换每一个约束，该公式定义了同样的解空间。

这会促使负的系数被去掉，并且既然能保证那些最小的值为0，那么公式（7）的计算就变得容易很多。在B&B算法在预处理阶段计算下限是很普遍的，在这里没有使用启发式算法，因为就像2.1中所提到的那样，希望该算法在遍历过程中尽快获得近似最优解。

2.4 存储复杂度分析

由于是深度优先遍历，最多有g个激活节点，g是类的个数，也是树的深度。对于每一个约束保持它的消耗数量，因此，对于整个遍历就消耗了O（mg）的内存。另外，对于第3种fathoming实验，在LMCKP的根部保持凸线计算以便进一步的应用。因为有O（ng）条线，总的来说，算法的空间复杂度是O（（m+n）g）。

3 计算结果

为了实地检验算法的应用效果，用C++编程、在P43.4 GHz、1 GB内存的的计算机上运行。并基于Coin CLP library（Coin-OR项目，2008）数据集处理LMMKP问题和计算双值。将文中的算法和 EMKP 算法（Sbihi，2007）进行比较，EMKP 算法目前是处理MMKP公认的最好算法。还与默认设置下得CBC算法（Coin-OR project，2008）进行比较，该算法是通用分支切割框架。这3种算法的可用内存都是512 M，给定运行时间是1个小时。

为了检测算法的效果，不但使用通用的MMKP问题实例，也使用自己生成的实例。Han et al.（2010）研究了怎样生成较为困难的MMKP问题实例。结果，他们得到了很多获益和权重之间具有不同相互关系的实例，而且这些实例的约束的松紧程度也不同。这些实例可以在网站Http://enstb.org/～gsimon/resources/MMKP/上找到。所有这些实例，都有g=10，n=5，m=5。表1比较了这3种算法在这些实例上的运行时间。Han et al.的实例基于它们的生成方法分类。每种分类下有100～2 000个实例。在每类方法中，报告了该算法基于实例运行时间的平均和标准偏差。基于核的算法标准差较小，这说明算法在实例上运行稳定。事实上，基于核的算法在处理一个实例时花费的最大时间是0.24 s，而EMKP和CBC算法却花费了26.22 s和1 889.41 s。比较而言，EMKP算法处理复杂实例的能力比CBC强，这得益于它的最佳优先遍历策略。但对于简单实例，CBC算法要优于EMKP。对于当前案例，有46 000个不同难度级别的实例，从处理结果看基于核的算法效果突出。表1是根据Han et al.提供的不同种类的实例，以秒为单位算法的平均运行时间 （标准偏差）。每种至少包含100个实例。

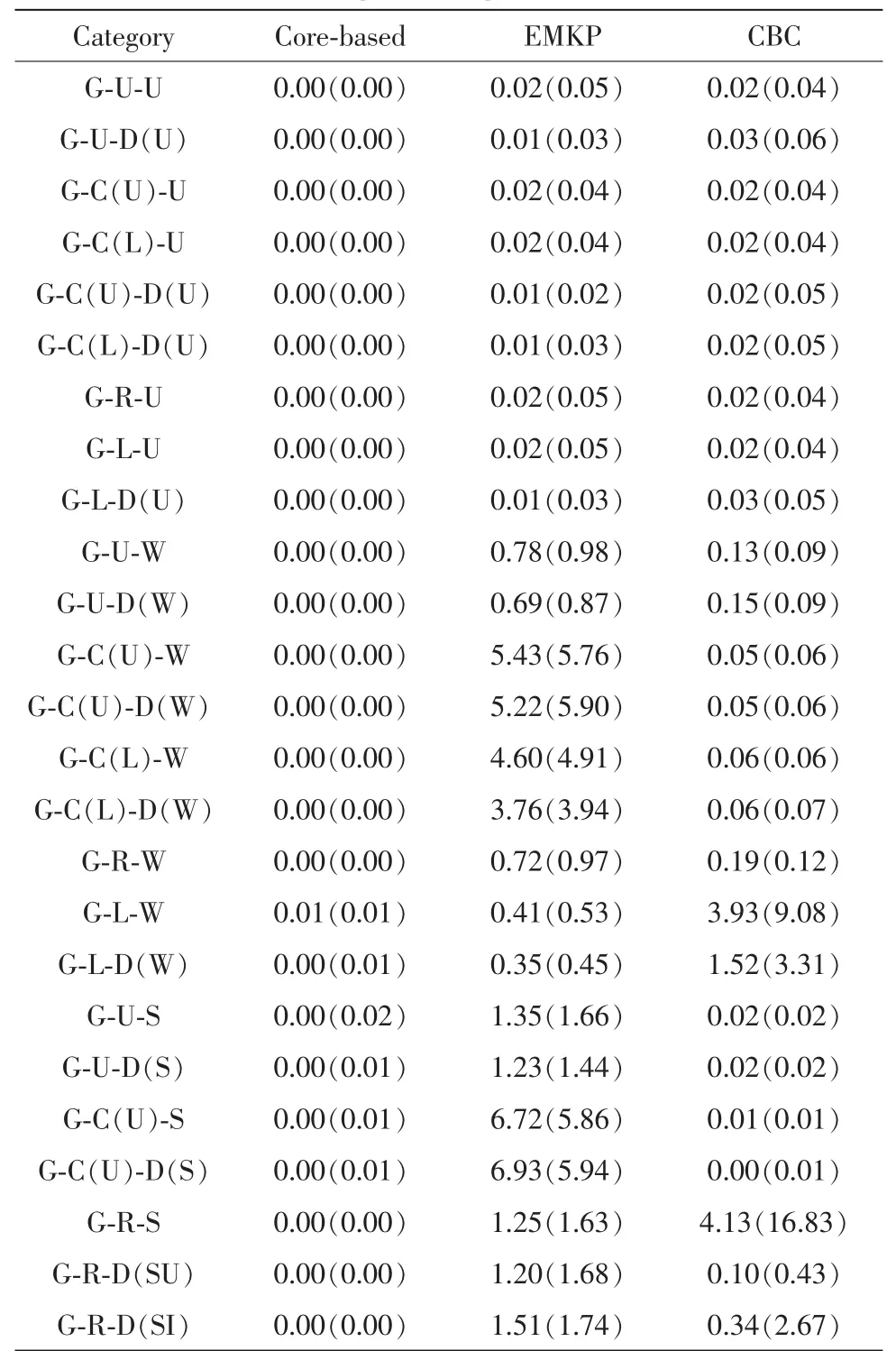
表1 实例的平均运行时间Tab.1 Average running time of instances

4 结 论

文中论述了一种精确解决多维多选择背包问题（MMKP）的B&B算法。首先为MMKP问题指明一个核，就是把关联LMCKP问题的解作为基本点，同时根据倾斜变换线和检验数分别对问题的类和元素进行排序，依次来定义这个核。是根据核中定义的排列顺序来生成B&B树，树的遍历采用深度优先算法。修剪子树需要有3个步骤：检测混合替代约束；检测可行性；检测由关联LMCKP辅助下计算得到的上限。我们还使用了变量固定和约束排序等辅助手段以提高算法的性能。计算结果显示，基于核的算法在处理MMKP问题时性能优于以往任何算法，特别是对于无关联和少约束实例。

[1]Wilbaut C，Hanafi S.A survey of effective heuristics and their application to a variety of knapsack problems[J].IMA Journal of Management Mathematics，2008（19）:227-244.

[2]Boyer V，Elkihel M，Baz D.Heuristics for the 0-1 multidimensional knapsack problem[J].European Journal of Operational Research，2009，199（3）:658-664.

[3]Tamir A.New pseudopolynomial complexity bounds for the bounded and other integer Knapsack related problems[J]，Operations Research Letters，2009，37（5）:303-306.

[4]Hsu C H，Tsou C S，Yu F J.Multicriteria tradeoffs in inventory control using memetic particle swarm optimization[J].International Journal of Innovative Computing，Information and Control，2009，5（11-A）:3755-3768.

[5]刘文涛，胡家宝.求解0-1背包问题的改进排挤遗传算法[J].计算机工程与设计，2011，32（6）:102-108.LIU Wen-tao，HU Jia-bao.Improved crowding genetic algorithm for 0-1 knapsack problem[J].Computer Engineering and Design，2011，32（6）:102-108.

[6]邓长寿，赵秉岩，梁昌勇.混合二进制差异演化算法解0-1背包问题[J].计算机工程与设计，2010，31（8）:220-226.DENG Chang-shou， ZHAO Bing-yan， LIANG Chang-yong.Hybrid binary differential evolution algorithm for 0-1 knapsack problem[J].Computer Engineering and Design， 2010，31（8）:220-226.