基于双核Nios II系统的数字预失真器设计*
2012-08-13曾德军石栋元李金政何子述
曾德军,石栋元,李金政,夏 威,何子述
(电子科技大学 电子工程学院,四川 成都611731)
在现代无线通信系统中,功率放大器(PA)是整个发射机中最为关键的部件之一。然而,PA固有的非线性特性会对通信质量造成严重影响。数字预失真技术作为一种高效的功放线性化方法,近年来得到了广泛重视和研究[1-4]。
传统的数字预失真器一般采用FPGA+DSP的方案,结构较为复杂,成本较高。本文在FPGA芯片中构建了SoPC系统,设计了一个自适应数字预失真器(DPD),它具有集成度高、成本低等优点。同时,采用并行RLS算法提取DPD模型参数,降低了传统RLS预失真算法的复杂度。采用双核Nios II并行操作,提升了硬件处理速度,保证了预失真处理的实时性和敏捷性。
1 DPD多查找结构
本文采用记忆多项式模型[5]作为DPD的行为模型,表示为:

其中,x(n)和z(n)分别代表DPD的输入和输出信号,akq为记忆多项式模型参数,K为多项式阶数,Q为记忆深度。
实现式(1)的方法是将其表达成基本预失真单元(BPC)的组合形式,如图1所示。其中,表项值函数的表达式如下:

本文使用间接学习结构[6]提取DPD的参数 akq,通过参考文献[6-7]的推导可知,参数提取方程总可以转换成如下形式:

其中,a=[a10,…,aK0,…,a1Q,…,aKQ]T为 DPD 参数向量;U=[u10,…,uK0,…,u1Q,…,uKQ]为与输入信号有关的输入矩阵;z为与期望信号有关的向量。考虑到参数计算数值稳定性问题和DPD对突变环境的适应能力,工程上一般采用自适应算法求解式(3)。

2 并行RLS算法及其Nios II实现
RLS算法作为一种应用极为广泛的自适应算法,具有性能优越、收敛速度快等优点。然而,传统的RLS算法涉及到大量的高维矩阵操作,算法复杂度高。本文根据参考文献[8]的思想,对传统RLS算法进行改进,生成并行RLS算法,并将其运用到DPD模型的参数提取过程中。
并行RLS算法的核心思想是将n时刻矩阵U的向量元素 u(n)以及 DPD参数向量 a(n)划分为 q组子向量,分别为 ui(n)、ai(n),其中 i=1,2,…,q,进而生成子滤波器组。采用自适应算法对各组子滤波器分别更新,更新完成后再将各子滤波器的权向量重新组合成一个完整的权向量,即aopt(n)。并行 RLS算法的步骤如表1所示。已知条件为:新输入向量u(n),权向量 a(n-1),期望信号 d(n),矩阵 P(n-1)。

表1 并行RLS算法步骤
表2对比了传统RLS算法与并行RLS算法在加法和乘法运算量上的差异。相对于传统RLS算法,并行RLS算法的最大优势在于降低了矩阵维数,故减小了运算复杂度。
从表2可知,并行RLS算法的q值越大,算法复杂度的优化程度越高。然而,多次仿真实验证明随着q值的增加,并行RLS算法的收敛速度会变慢,性能也会受到影响。经过综合权衡后,本文使用q=2时的并行RLS算法,并采用双核Nios II进行实现,其架构如图2所示。

表2 传统RLS与并行RLS算法的运算量

在并行RLS算法中,主要的滤波过程和算法更新过程都是完全独立的,可以在CPU1和CPU2中并发执行。并行RLS算法涉及到的交互数据放在共享存储区内,双核可以通过互斥机制访问。
图3为基于查找表的DPD在双核Nios II系统中的实现结构。该系统的工作状态可以经历如下阶段:
(1)DPD学习过程:DPD不加入传输链路,基带信号直接上变频后输送至PA,双核Nios II收集基带信号和PA反馈信号。
(2)并行RLS算法处理过程:双核Nios II按照图2的步骤求解出DPD模型参数向量a。

(3)查找表更新过程:将a的元素值代入方程式,通过双核Nios II计算出查找表的表项值,并将表项值写入查找表RAM中,完成更新。
(4)DPD工作过程:DPD加入传输链路,构成DPD+PA的完整预失真系统。基带信号通过查表完成预失真操作。
3 系统功能验证
本实验中采用的功放的中心频率为710 MHz,线性增益为43 dB,1 dB压缩点为-8.5 dBm;DPD模型的多项式阶数为3,记忆深度为2,输入到PA的测试信号是具有5 MHz带宽的WCDMA信号。
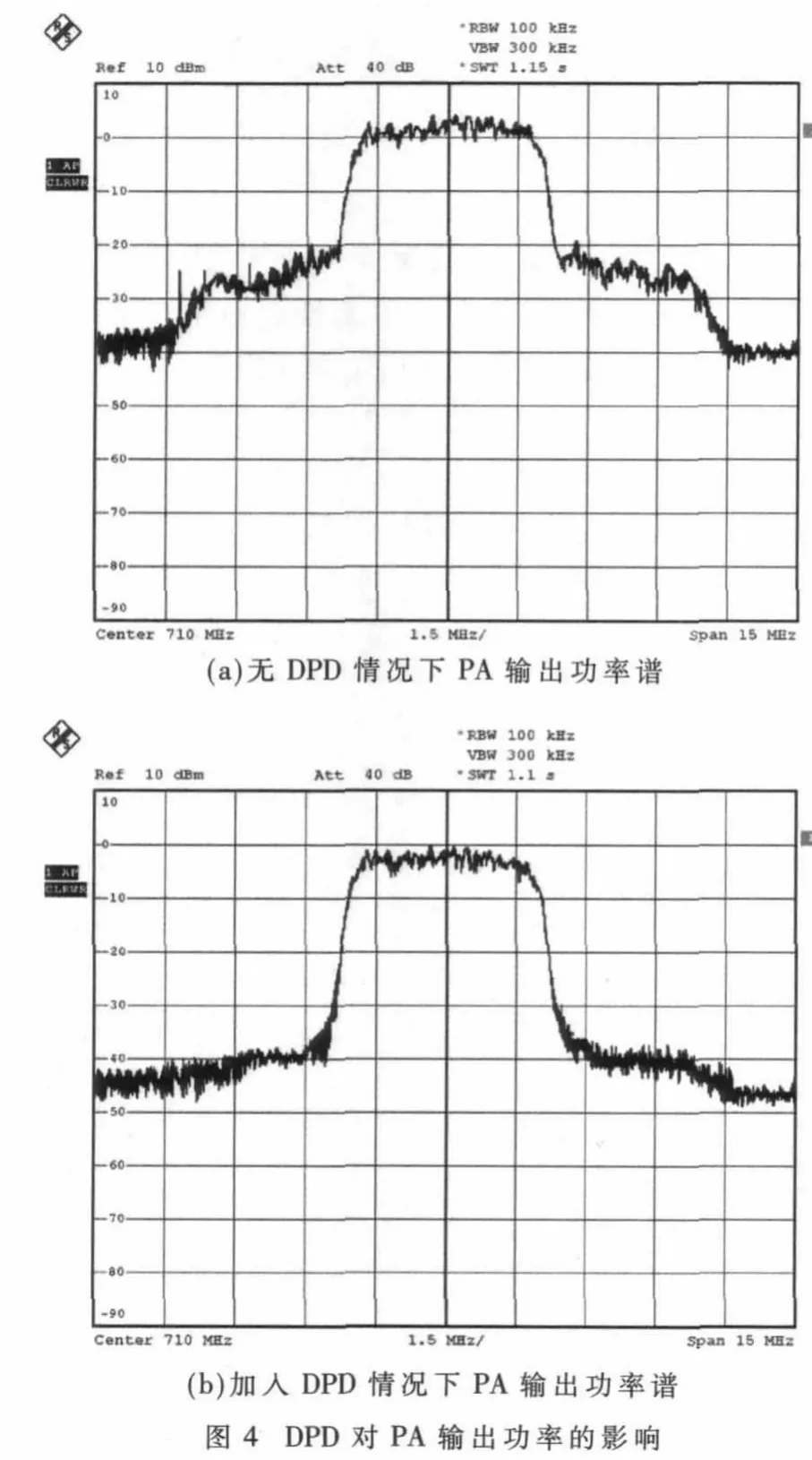
通过图4和表3可见,WCDMA信号在未加入DPD前,其邻道频谱干扰严重,ACPR只有19 dB。但加入DPD后,信号的带外杂散信号得到抑制,且ACPR改善量在15 dB~20 dB之间。同时,加入DPD后系统的NMSE得到明显改善,WCDMA信号带内失真得到了控制。实验测试表明,DPD的预失真效果理想,达到了预期设计目的。
本设计在FPGA芯片中实现了一个基于双核Nios II的自适应数字预失真器(DPD)。该系统稳定可靠,能够对功放的非线性进行较好的补偿,且能够抑制信号经过功放后的带外频谱滋生,同时提高了信号在带内频谱的平坦度。

表3 WCDMA信号下DPD系统实测性能
[1]HONG S,WOO Y Y,KIN J,et al.Weighted polynomial digital predistortion for low memory effect doherty power amplifier[J].IEEE Transaltions on Microwave Theory and Techniques,2007,55(5):925-931.
[2]YOUNES M,HAMMI O,KWAN A,et al.An accurate complexity-reduced “PLUME”model for behavioral modeling and digital predistortion of RF power amplifiers[J].IEEE Transactions on Industrial Electronics,2011,58(4):1397-1405.
[3]GUAN L,ZHU A.Dual-loop model extraction for digital predistortion of wideband RF power amplifiers[J].IEEE Microwave and Wireless Components Letters,2011,21(9):501-503.
[4]GILABERT P,MONTORO G,BERTRAN E.FPGA implementation of a real-time NARMA-based digital adaptive predistorter[J].IEEE Transactions Ciruits And System,2011,58(7):402-406.
[5]DING L,ZHOU G T,MORGAN D R.A robust digital baseband predistorter constructed using memory polynomials[J].IEEE Transactions on Communication,2004,52(1):159-165.
[6]刘宁.功放数字预失真算法研究及硬件实现[D].成都:电子科技大学,2011.
[7]GILABERT P L,CESARI A,MONTORO G,et al.Multilookup table FPGA implementation of an adaptive digital predistorter for linearizing RF power amplifiers with memory effects[J].IEEE Transaction on Microwave Theory and Technigues,2008,56(2):372-384.
[8]CHATURVEDI A K,SHARMA G.A new family of concurrent algorithms for adaptive volterra and linear filters[J].IEEE Transactions on Signal Processing,1999,47(9):2547-2551.
