基于压缩感知解码的网络编码技术

高 超， 李生红， 唐俊华

（上海交通大学 电子信息与电气工程学院，上海，200240）

0 引言

在 R. Alshwed等人提出了网络编码[1]的概念之后，网络编码吸引了众多研究者的兴趣。在文献[1]中，作者证明了网络编码可以使网络容量达到最大流-最小割定理的理论上界。在此之后，网络编码的容量和组网方法又成为了研究的焦点。文献[2]中描述的无差错网络的线性编码代数模型证明了多播网络编码的存在。随机网络编码作为一种可行的分布式编码方案，在文献[3]中进行了详细讨论，证明了当所有的编码系数是从一个有限域中按照均匀分布的概率随机抽取时，可以以很高的概率得到一个可解码的网络编码。当网络编码不可解码时，其传输矩阵可视为一个欠定方程组的系数矩阵。借助压缩感知的思想，网络可解码的概率可以进一步增加。

压缩感知[4]是一种新的对稀疏信号的采样重建方法。Candes和Donoho等人证明了对于稀疏信号，可以采样部分信号，并利用采样通过一定的方法重建[5-6]。压缩感知的核心在于感知矩阵，也称为测量矩阵。Candes和Tao等人证明了满足有限等距性(RIP,Restricted Isometric Property)的矩阵可以用作感知矩阵。在随机网络编码中，传输矩阵的子矩阵具有RIP性质。仿真结果表明，压缩感知可以用于随机网络编码的解码。

1 系统模型

考虑单源单信宿的无误差无环网络。用一个有向图G=(V, E)表示此网络，V为顶点集，E为边集。每条边的容量为单位容量。如果两个节点之间实际容量大于 1，则用多条边表示。文献[2]中描述了这种模型。每条边用一个整数表示。可以用一个三元组e=(vi, vj, k )表示。如果一条边e终止于定点v，定义：

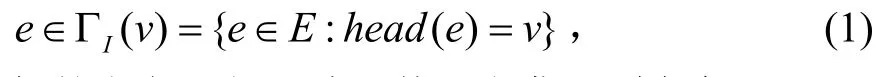
用类似的定义，如果边e从v出发，则定义：

用Y( e)表示边e传输的信息。

在具有L条边得线性网络编码中，网络可以用一个L×L的邻接矩阵表示。矩阵元素 fij∈Fq是有限域Fq中的元素。在每一个节点v处，每条边ej∈Go(v)传输顶点v所收到信息的线性组合：

因此邻接矩阵F表示了组合系数。假设信源节点s以恒定速率R生成离散的整数序列X(s)，序列中的整数也是有限域Fq的元素。在源节点s看来，所产生的信息序列可以看成来自一组虚拟边ei∈ΓI(s), i=1,2,…,n 的输入的线性组合，n为s和信宿节点d之间的最小割。对于每一条边ej∈ΓO(s)，Y( ej)等于Y( ei),ei∈ΓI(s)的线性组合，即：

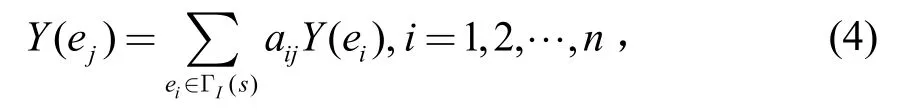
aij是组合系数，所有的系数组成一个n×L矩阵A。在信宿节点，定义一个L×n矩阵B，它的元素为信宿节点的所有输入的线性组合系数：

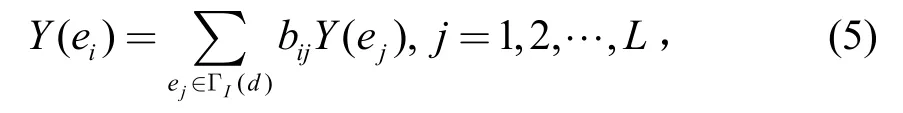
最后，可以得到传输矩阵：

文献[2]提出了随机网络编码(RNC, Random Network Coding)。RNC中，矩阵A、F和B的元素都是独立地从有限域Fq中随机抽取的。文献[3]证明了信宿节点能以概率(1d/q)h-成功解码。其中d为信宿节点数，h是边数。

在文献[7]中，作者讨论了一种实用的编码方案。该方案中，每一条边不仅传输线性组合，也同时传输组合系数，称为全局向量。因此每条边传输的实际上是一个方程yi=gix。在每个节点中，输出的系数向量是所有入向量的线性组合，其组合系数与信息的组合系数相同。信宿节点把收到的所有输入向量进行组合，可得到线性方程组y=Gx，G的每一行都是一个全局向量g。

在信宿节点d中，每一条输入边中传输矩阵G=(A( I-F)-1BT)T的一行，其中：

2 压缩感知解码

2.1 压缩感知

当前的随机网络编码不可解码的概率为1-(1-d/q)h。在实际应用中[8]，如果信宿节点不能成功解码，那么已经收到的信息会被丢弃，这样会造成传输延时。

然而，如果信息序列x是稀疏的，根据文献[5]，可以利用压缩感知来尝试解码。如果传输矩阵G的秩是m，可以取出G中线性不相关的m行以及对应的信宿节点收到的m个信息y'，组成一个欠定方程组y'=Φx，Φ是一个m×n矩阵。压缩感知求解的问题可以如下描述：

研究表明Φ具有文献[5]所定义的有限等距性，因此可以进行压缩感知。信宿节点首先执行一般的解码，即直接求解方程组y=Φx。如果G不可逆(不满秩)，则构造Φ并执行压缩感知解码算法。有多种算法可以用于压缩感知的解码[9-10]。

2.2 分析

在图G=(V, E)中，按照信息传输的顺序为每一条边e编号。因此A和B可以写成:

邻接矩阵F是一个对角线元素全零的上三角矩阵。因此(I-F)-1可以写成I+F+F2+…+Fn，定义F(m)=Fm,m∈ℤ+，有：

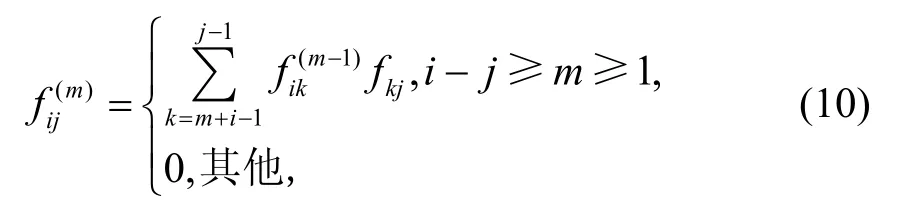
为了得到感知矩阵Φ，定义Ψ=(I-F)-1，并且有：

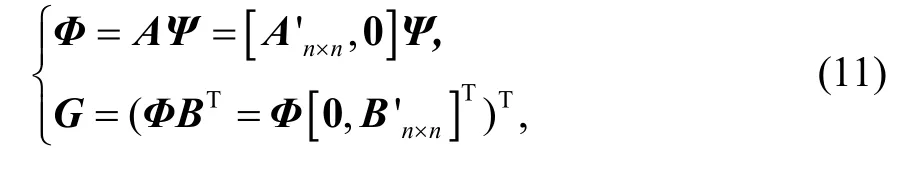
由于B有n个非零行，每个非零行只含有一个 1，因此G由Φ得最后n列组成。令ai，φj分别表示A的第i行和Ψ的第j列，可得到：

在压缩感知解码中，从G中随机选取k个不相关行组成一个k×n矩阵H。可以由H计算误码率。一个稀疏度为s的向量nx的误码率由下式确定：

现在考虑yk=Hzn的概率。令m=||xn||0，文献[11]证明了该事件的概率为：

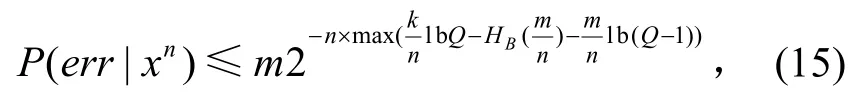
定义PCS fails=P(err|xn)，其含义为压缩感知解码失败的概率。

对于随机网络编码，常规解码与压缩感知解码是独立的。由于只有当常规解码与压缩感知解码全部失败时，网络编码才被视为不可解码，因此误码率为：

3 仿真与结果

仿真结果重点在与观察有限域大小和稀疏度对压缩感知解码的影响。图1表明，误码率随着有限域增大而降低，而CS-RNC比单纯的RNC误码率性能较优。

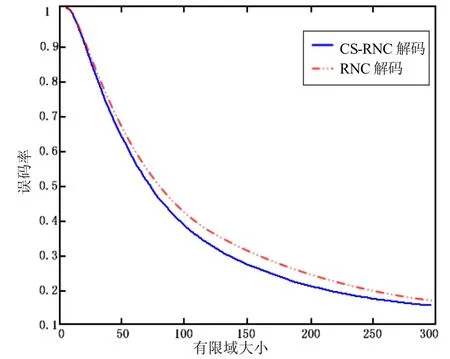
图1 误码率与有限域大小的关系

4 结语

随机网络编码的传输矩阵满足RIP条件，对于稀疏的信号，可以采用压缩感知的方法进行解码。对于单播情况，信宿可以同时采用一般的网络编码解码和压缩感知解码结合，以提高解码成功率。当随机网络编码的编码系数所在的有限域较小时，压缩感知解码可以明显提高成功率。当有限域扩大时，其成功率下降，但一般的网络编码解码成功率反而会增加，而且增加的更快。因此总的成功率也会增加。下一步的研究方向是寻找更适合压缩感知的随机网络编码方法。

[1] AHLSWEDE R, CAI N, LI S Y R, et al. Network Information Flow[J]. Inform. Theory, 2000, 46(04):1204-1216.

[2] KOETTER R, MEDARD M. An Algebraic Approach to Network Coding[J]. Proc. IEEE Int Information Theory Symp, 2001, 16(04):204-216.

[3] HO T, MEDARD M, SHI J, et al. On Randomized Network Coding[J]. In Proceedings of 41st Annual Allerton Conference on Communication, Control, and Computing, 2003, 12(05):689-709.

[4] 李晖，郭长顺，常全成. 基于矩阵分解的压缩感知算法研究[J]. 通信技术，2011,44(09):108-110.

[5] CANDES E J, ROMBERG J, TAO T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].Inform. Theory, 2006, 52(02):489-509.

[6] TSAIG Y, DONOHO D L. Compressed Sensing[J]. IEEE Trans. Inform. Theory, 2006, 52(04): 1289-1306.

[7] YUNNAN P C, CHOU P A, WU Y, et al. Practical Network Coding[J]. Inform. Theory, 2003, 12(01):419-439.

[8] 王蓟翔，张扬. 无线传感器网络 MAC协议的研究与改进[J]. 通信技术，2011,44(06):138-143.

[9] CANDES E J,TAO T. Decoding by Linear Programming[J].Inform. Theory, 2005, 51(12):4203-4215.

[10] DONOHO D J, TANNER J. Thresholds for the Recovery of Sparse Solutions via l1 Minimization[J]. Proc.40th Annual Conf. Information Sciences and Systems,2006, 11(05): 202-206.

[11] DRAPER S C, MALEKPOUR S. Compressed Sensing over Finite Fields[J].Proc. IEEE Int. Symp. Information Theory 2009, 21(13): 669-673.