一种用小波包变换提取眼电信号警觉度特征的方法

高春芳 吕宝粮 马家昕

1(皖南医学院医学二系麻醉与影像设备学教研室，芜湖 241002)

2(上海交通大学计算机科学与工程系仿脑计算与机器智能研究中心，上海 200240)

3(上海交通大学智能计算与智能系统教育部-微软重点实验室，上海 200240)

4(上海交通大学上海市可扩展计算与系统重点实验室，上海 200240)

5(京都大学工学研究科机械工程与科学系，京都府 6293558，日本)

引言

警觉度(vigilance)是指人集中注意力执行某项操作任务时所表现出的灵敏程度。为了保证系统或车辆的运行安全，对某些工作岗位的操作人员，如高铁司机、危险品运输司机和长途客车司机等，需要进行实时的警觉度估计和预测。因此，警觉度估计和预测是人机交互和主动安全技术领域的一项重要研究课题。已有的警觉度估计和预测方法可分为两类：一类是基于人的行为特征，如面部表情、眼睛闭合程度等;另一类是基于人的生理信号，如脑电(electroencephalogram，EEG)、眼电(electrooculogram，EOG)和皮肤阻抗等。前者是通过数字图像处理技术提取特征来估计警觉度[1]，其优点是获取数据时不需要接触人体并且数字图像处理技术比较成熟，如用摄像头测定眼睛闭合时间占眨眼总时间百分比的 PERCLOS方法[2]。但是，此类方法的缺点是容易受到光线变化、佩戴眼镜和墨镜的影响以及疲劳度量的时间窗口太长等问题。后者是通过生理信号特征来估计人的警觉度状态[3-5]，其优点是准确率高且无法伪装等。其中，基于EEG的检测方法被认为是疲劳检测的“金标准”。但是，生理信号的采集需要接触人体。

EOG记录的是视网膜与角膜之间的电位差，以及眼球运动时眼动肌所产生的电位。EOG信号的采集是通过将两对电极分别放置在左右眼的外侧和一只眼睑的上下侧位置实现的。相比于EEG信号的采集，EOG所需电极数少、电极安放简单且放置处无毛发干扰。在信号强度方面，EEG是微伏级，而EOG是毫伏级。与 EEG相比，EOG信噪比高，对信号放大器要求低。

EOG与EEG都是睡眠研究中用来检测睡眠阶段的标准信号，而警觉度与睡意有紧密联系，因此EOG被认为是一种能够直接反映警觉度状态变化的生理信号。Wright等开展了飞行员警觉度的研究，他们的研究结果表明，EOG和EEG能够比较精确地反映警觉度的变化[6]。Hanke等分析了 EOG信号的幅值、幅值的一阶导数、傅里叶变换后的低高频比等3种特征，他们的实验结果显示，低高频比最能反映警觉度状态[7]。Magosso等用小波变换检测EOG信号中的慢速眼动并分析慢速眼动在睡眠分类上的作用[8]。Khushaba等人基于小波包变换的模糊集理论，对人体的EEG、EOG、ECG等信号进行特征提取，用来对驾驶员的疲劳状态进行分类[9]。蔡浩宇等提出了前额EOG信号采集方法，避免了传统方法在眼睛周围放置电极，影响视野的问题[10]。这种前额 EOG采集方式较传统 EOG采集方式更为便利，适合于基于眼电信号警觉度估计与预测的实际应用和高铁司机等用户的佩戴。

基于EOG的警觉度估计与预测研究的一个基本问题是如何找出与警觉度最为关联的特征。马家昕等分析了慢速眼动、快速眼动以及眨眼等11种警觉度特征，其中相关度最大的是慢速眼动傅里叶变换能量比(SEMe)特征，35组实验结果的平均相关度是0.703[11-12]。本研究在马家昕等的研究基础上，应用具有时-频细节分析优势的小波包变换方法，提取EOG信号的低高频能量比特征，以期找出眼电信号中更为有效的警觉度特征。

1 特征提取方法

1.1 小波包变换理论

小波变换(wavelet transform)是将信号分解成低频近似部分和高频细节部分，在后续只对低频部分做分解，而不对高频部分进行分解，从而导致高频部分频率局部性不好。小波包变换(wavelet packet transform)方法借助于小波分解滤波器，在各个尺度上对低、高频子带均进行二次分解，如图1所示。小波包变换的优点是提高了信号高频部分的频率局部性，对信号的分析能力更强[13]。

图1 小波变换与小波包变换比较。(a)小波分解树;(b)小波包分解树Fig.1 Comparison of wavelet transform with wavelet packet transform.(a)Wavelet tree;(b)Wavelet packet tree

在尺度j下，每个节点对应的能量定义为

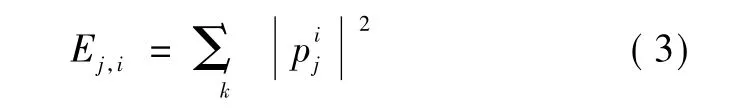
小波包重构是指，第j层上的第i个小波包是第j+1层上的第2 i和第2 i+1个小波包隔点插零后分别与小波重构滤波器h、g卷积之和，如式(4)所示。

小波包变换对各层的高频部分继续利用分解滤波器H和G进行再分解，其后续的子带频带是交错的。以原始信号采样频率为128 Hz为例，对其进行3层小波包分解。第一层(1，0)节点频带为0～32 Hz，(1，1)节点频带为32 ～64 Hz。对高频带(1，1)节点进行下一层分解，频带会出现交错，即(2，2)节点频带为48～64 Hz，(2，3)节点频带为32～48 Hz。所有高频子带的再次分解，都会出现此类频带交错，在重构不同频带信号时，要注意频带的交错。

小波(包)变换中涉及到小波基的选择，对于EOG分析，有学者用过 daubechies小波(dbN)和symmlets小波(symN)[8-9]。本研究采用了 db4、sym4和bior2.4等3种小波基，但后续的实验结果表明，这3种不同的小波基对警觉度估计基本没有影响。

1.2 能量比计算

所提出的能量比特征定义为：EOG信号低频段与高频段能量的比值。比值的特点是消除了个体总能量的差异，体现了个体EOG中不同频段能量的比例关系。已有的研究表明，在微睡状态下，慢速眼动成分会相对增多[8]，而微睡预示着警觉度下降。慢速眼动的频率范围是0.2～0.6 Hz，而眼电信号的频带范围是0～30 Hz。基于这些特点，考察了16种不同的低、高频段能量比，以期找出与警觉度相关的能量比最优分段。这16种能量比分段及其对应的小波包节点如表1所示。

每个特征值的低频段能量值Lfi和高频段能量值Hfi可根据式(3)写出相应表达式，特征值 Fi由低、高频段能量值取常用对数后再相除得到。以F6为例，相应表达式分别如式(5)～式(7)所示，其他Fi可依此类推。

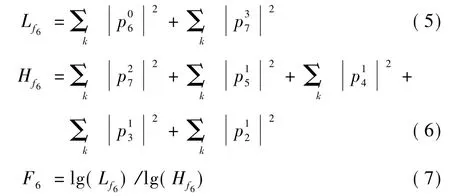
1.3 特征去噪

上面所获得的警觉度特征值，在以秒为单位的分辨率上波动幅度较大。而在实际情况中，警觉度的变化是缓慢、有规律的，故需要对特征值进行去噪处理。最常见的是滑动平均(MA)去噪，即取某一时间窗内的平均值作为该时间窗中点处的值。该方法简单易行，但窗口的大小对去噪结果影响比较大。窗口大，去噪效果好，但时间延迟长;反之，窗口小，去噪效果差。

线性动力系统(linear dynamical system，LDS)是一种状态空间模型，可以实时去噪[14]。系统的模型结构如图2所示，其中Zi是隐变量，即按一定规律变化的实际状态值;Xi是观测变量，即实际观测到的值，包含了观测噪声。

表1 16种能量比特征的频带分段及对应的小波包节点Tab.1 The range of frequency about 16 energy ratios and the corresponding wavelet packet nodes

图2 线性动力系统模型结构图示Fig.2 The schematization of LDS

由于噪声的影响，Xi之间无法直接得到时序上的变化关系，但是Zi在时序上是有直接关系的。此模型通过隐变量之间的关系、以及隐变量与观测变量之间的关系，推断出当前时刻的隐变量的概率分布。为便于公式推导，假设这两类变量都是高斯分布的连续变量。

在确定了第二日列车运营日计划模板后，为模板中相应的列车车次编配状态良好的车组，称为列车运营日计划编配。目前传统的人工编配方式存在生产效率低下、安全隐患大等问题，因此，科学地进行列车运营日计划编配具有重要现实意义。

设隐变量之间的关系为

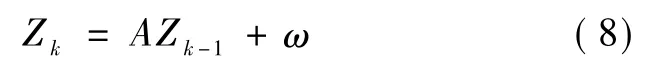
隐变量与观测变量之间的关系为

式(8)和式(9)中，A和C为转换矩阵，ω为隐变量之间的传递波动，v为观测变量与隐变量之间的传递波动(也可视为观测噪声)，这些波动都满足均值为0的高斯分布

隐变量的初始值Z0的概率形式设为

式(8)为隐变量的递推形式，其概率形式可表示为：

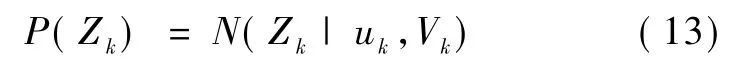
式中，uk、Vk都是从系统中推断出来的。

整个系统包含 6 个参数：u0，V0，A，Γ，C，Σ。其中，u0、V0是隐变量初始值 Z0的概率分布，在实验中，将Z0设置为待处理数据前20 s的平均值;A和C是转换矩阵，是隐变量与隐变量、隐变量与观测变量之间的转换，在本文的应用中，特征值并没有逐渐放大或逐渐缩小的趋势，故令其值都为1;Γ、Σ是隐变量、观测变量的高斯分布的方差，这两个值由交叉验证得出。

在降噪过程中，实际需要的是隐变量序列{Zi}的值，Zi是满足高斯分布的，其概率分布中可能性最大的值是 Zi的均值 ui，即最后需要的是序列{ui}的值。线性动力系统包含两个关键算法，分别是递推算法和学习算法，前者用来修正{ui}，后者用来确定模型中所有参数θ的值。LDS的效果如图3所示，这里变化剧烈的非警觉度成分已被过滤掉。

图3 LDS效果图：剧烈波动的线形为 LDS处理之前，平滑的线形为LDS处理之后的结果Fig.3 The effect of LDS，where the sharp line is the one before LDS，and the smooth line is the one after LDS

1.4 实验

实验被试者均为上海交通大学在读学生，共22名。其中男14人，女8人，平均年龄22岁，身体健康，右利手。实验前一天，被试者需限制睡眠时间，一般不超过6 h，不能饮用酒、咖啡等刺激性饮料，知情研究目的。实验在午餐后的13：00～15：00进行，此时人体最容易产生困倦感，以便被试在实验过程中能经历从清醒到瞌睡的完整过程。整个实验过程约为70 min，部分被试参与多次实验，同一被试两次测试时间间隔为一周以上。

实验设备包括 NeuroScan系统(4.3版本)和Stim2系统(2.0版本)两大部分(Compumedics公司，澳大利亚)。被试头戴62导脑电帽(M1、M2电极未使用)，眼部上、下、左、右佩戴4个传统眼电电极，额头上方佩戴4个前额眼电电极，如图4所示。NeuroScan系统通过上述电极收集脑电信号、传统眼电信号以及前额眼电信号。Stim2系统用于产生刺激序列并记录测试者的按键情况，即错误率。实验中的场景如图5所示，电脑屏幕上每5～7 s随机出现红、绿、黄和蓝等4种颜色共170种交通指示图片中的一个(如图6所示)，图片显示时间为500 ms，被试手持按钮盒，并按压盒上相应颜色的按钮，按键的正确与否被Stim2系统记录下来(没有按键也算是错误)。系统每8 s得出一个错误率数值，该值是以8 s时间段为正中间段前后共120 s内按键错误率的平均值，数值范围为0-1，数值越大，表示警觉度越低。用错误率来作为警觉度的标识(vigilant label)，能够对实验中被试的警觉度状态进行客观、实时的标记，比其他主观判断警觉度状态的方法要更为精确。

图4 被试佩戴脑电帽、传统眼电电极以及前额眼电电极Fig.4 The testee wearing the electrodes of EEG，traditional EOG and forehead EOG

图5 实验场景Fig.5 The experiment scene

1.4.2 数据采集与预处理

图6 4类不同颜色的交通指示图片(红、黄、蓝和绿)Fig.6 Traffic signals’pictures of four kinds colors(red、yellow、blue and green)

实验中 NeuroScan系统记录的数据是62导EEG，4导传统眼电 EOG(眼睛上下电极是垂直眼电，左右电极是水平眼电)，4导前额眼电，采样率为500 Hz，并进行0.1～100 Hz的滤波。在前述的特征值频率分段，实际起点应该是0.1 Hz，而不是0 Hz。Stim2系统记录被试的错误率，采样频率为0.125 Hz。两者保持同步记录。预处理时，进行人工目测信号，舍弃低SNR信号，将EOG信号降采样到125 Hz。

1.4.3 实验结果分析

收集35组有效实验数据，取水平EOG信号，时间窗设定为8 s，小波包母函数分别采用 db4、sym4和bior2.4，小波包分解阶数为8。根据1.2中叙述的方法，计算特征值F1～F16，对获得的特征值分别进行滑动平均(120 s、80 s和40 s)去噪和线性动力系统(LDS)去噪处理，最后将特征与错误率做相关分析，得出相关系数。

2 实验结果与分析

小波包母函数的影响如图7所示，图中的3条曲线分别代表小波包母函数采用 db4、sym4和bior2.4，3条曲线基本没有差别，尤其是在 F5、F6处曲线上的点完全吻合。在比较分析中发现，不同的小波包母函数对相关系数基本没有影响，但频带分段和去噪方式对相关系数的影响比较大。去噪方式的影响如图8所示，经120 s MA去噪后的平均相关系数最高，但120 s MA，有60 s的时间延迟，这对警觉度的即时估计与预测是不能接受的。次高的是LDS去噪处理，该去噪效果接近120 s MA，且没有时间延迟，便于实时估计和预测。稍差的是80 s MA处理结果。最差的是40 s MA处理结果，此方法得到的平均相关系数比 LDS的低13%左右，且40 s MA处理也是有20 s的时间延迟。综合处理效果和时间延迟等因素，LDS去噪处理方式是最佳的。频带分段的影响在图7和图8中都有体现，每条曲线的峰值都在F6处，即F6处的平均相关系数最高。在F6之前，相关系数是稳定地逐渐增高的;在F6之后，相关系数缓慢降低，降低幅度虽小，但降低的趋势基本不变。故频带最优分段在F6处，即(0～1.50 Hz)/(1.50～31.25 Hz)。

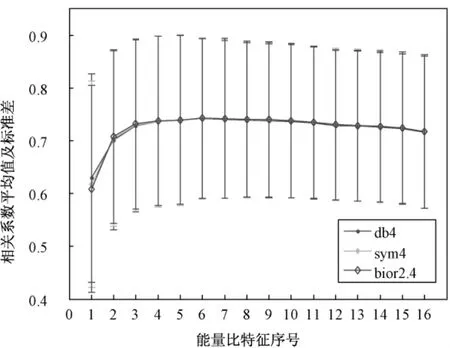
图7 由不同小波母函数得出的能量比特征的相关系数平均值及标准差Fig.7 The mean and standard deviation of coefficients about features from different wavelet function

图8 经不同的去噪方式处理后特征F1～F16的相关系数均值及标准差(小波基函数是db4)Fig.8 The mean and standard deviation of coefficients about features denoised by different ways(wavelet function is db4)

选择最优特征F6，经 LDS去噪，将其归一化到警觉度标记上。比较实验全程中特征值曲线与警觉度标记曲线的关系，图9给出了两次不同实验的结果。图中特征F6曲线与错误率曲线波形都很相似，尤其是在错误率大幅增高(即警觉度下降)处，特征值也显著增高，曲线峰值部分吻合很好。

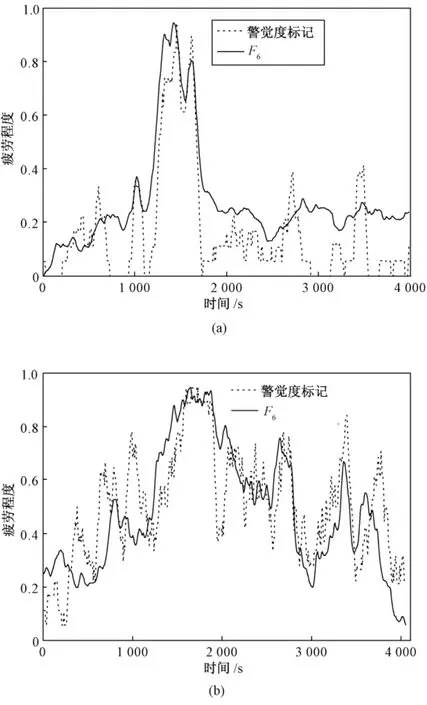
图9 特征值F6与警觉度标识的关系图(疲劳程度：0为清醒，1为睡眠)。(a)相关系数为0.864;(b)相关系数为0.744Fig.9 The relational graph between F6 and the vigilant label(zero is waking，one is sleeping).(a)The coefficient is 0.864;(b)The coefficient is 0.744

F6在35组实验上的相关系数平均值为0.742，标准差为0.151。与文献[12]中的慢速眼动、快速眼动以及眨眼等11个特征做比较，结果如图10所示。从图中可以看出，F6特征的相关系数平均值高于已有的11个特征，标准差也较小。

已有的11个特征中较好的特征有6个(相关系数平均值≥0.6)，分别是慢速眼动的小波变换判别函数特征(SEMf)、慢速眼动的傅里叶变换低高频能量比特征(SEMe)、眨眼的低高频能量比特征(BLKe)、闭眼速度特征(CV)、睁眼速度特征(OV)和闭眼时长特征(CLT)[12]。将特征 F6与这6个较好特征进一步进行配对t检验，检验结果如表2所示。表中sig值都小于0.05，表明特征F6与已有的特征在统计学上有显著性差异，能够更好地表征警觉度。

图10 F6特征与已有11个特征在相同35组实验上的相关系数平均值和标准差比较Fig.10 The contrast between feature F6 and the previous eleven features about the same 35 sets

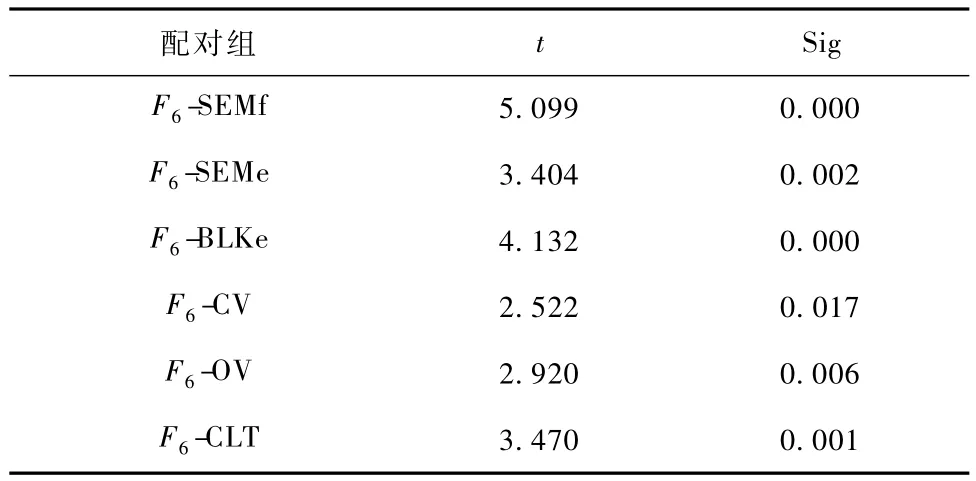
表2 F6特征与已有的较好的6个特征的配对t检验结果Tab.2 The paired samples test of F6 and the pre-existing six features

特征F6与警觉度的高相关性提示：能量信息是生理电信号的重要信息，可以从生理电信号的能量角度揭示人体的状态。频带分段为(0～1.50 Hz)/(1.50～31.25 Hz)的能量比特征与警觉度标记有最高的相关度，其生理学机理源于警觉度下降时尤其是进入微睡状态，EOG信号的慢速眼动成分会相对增多[8]，而慢速眼动的频率范围是0.2～0.6 Hz，即包含在频带的低频部分。后续可深入分析警觉度在各个阶段(如警觉度黄色预警状态、红色预警状态、红色警告状态等)EOG信号的主要频带，这样可以在能量比特征上分阶段设置频带分界点，以提高警觉度的估计和预测精度。

小波包变换获得带通能量比，与直接带通滤波后取能量包络的方法相比，小波包变换的时频细节特征更好，可以在选择低高频分割点的时候，以0.25 Hz(信号采样率128 Hz，小波包阶数为8，Δf=0.25 Hz)为步进进行分析，能更细致地寻找哪个分割点更好。用Matlab的小波包工具箱，计算上述特征F6值，1 h的眼电数据，在戴尔 Optiplex 360 miniTower，处理器是英特尔酷睿2双核 E7400，内存2 GB，英特尔 G33/G31集成显卡的电脑上进行处理，需要的时间约为80 s，占用的内存是1117 MB。

3 讨论和结论

实验中的相关因素在后续的研究中有待改进，如实验中的被试人群年龄集中在学生段，下一步可拓展到更广的成人年龄段。实验中的操作是在室内模拟驾驶环境下进行的图片按键，有别于实际驾驶环境。实验室正在建设真车驾驶环境，后续进一步验证该能量比值表征警觉度的能力。本文的实验结果表明生理电信号的能量比值较其他特征能够更好地表征警觉度状态，生理电信号的能量信息是生理状态的重要指标。在该结果的启示下，其他生理状态的研究，如情感识别等方面，相应电信号的能量也可能会提示重要信息，后续可拓展到其他生理状态的电信号能量研究。

本研究应用小波包变换方法，根据慢速眼动和EOG的频域特点，考察了水平 EOG的16种不同的低、高频段能量比警觉度特征。实验结果表明，低高频最优分段是(0～1.50 Hz)/(1.50～31.25 Hz)，由该分段所获得的能量比特征优于慢速眼动、快速眼动，眨眼等其他已有的11种警觉度特征。本文的实验结果进一步表明，EOG是一种能够表征警觉度的有效生理信号。在后续的研究工作中，将从EOG提取的这些不同的特征中选取警觉度估计和预测的最优子集，并在真实驾驶环境中验证其有效性。

[1]Ji Qiang，Yang Xiaojie.Real-time eye，gaze，and face pose tracking for monitoring driver vigilance [J]. Real-TimeImaging，2002，8(5)：357-377.

[2]Grace R，Byrne VE，Legrand JM，et al.A machine vision based drowsy driver detection system for heavy vehicles[C]//Proceedings of Conference on Ocular Measures of Driver Alertness.Washington DC：FHWA，1999：75-86.

[3]Makeig S，Jung TP.Changes in alertness are a principal component of variance in the EEG spectrum [J].Neuroreport，1995，7(1)：213-216.

[4]Kenneth P，Wright Jr，Joseph HT，et al.Relationship between alertness，performance，and body temperature in humans[J].American Journal of Physiology，2002，283(6)：1370-1377.

[5]傅佳伟，石立臣，吕宝粮.基于EEG的警觉度分析与估计研究综述[J].中国生物医学工程学报，2009，28(4)：589-596.

[6]Wright N，McGown A. Involuntary sleep during civil air operations：wrist activity and the prevention of sleep [J].Aviation，Space，and Environmental Medicine，2004，75(1)：37-45.

[7]Hanke S，Zeitlhofer J，Wiest G，et al.Automated vigilance classification based on EOG signals：preliminary results[C]//Proceedings of World Congress on Medical Physics and Biomedical Engineering.Munich：IFMBE，2009：428-431.

[8]Magosso E，Provini F，Montagna P.A wavelet based method for automatic detection of slow eye movements：A pilot study [J]Medical Engineering＆ Physics，2006，28(9)：860-875.

[9]Khushaba RN，Kodagoda S，Lal S，et.al.Driverdrowsiness classification using fuzzy wavelet- packet-based featureextraction algorithm [J]. IEEE Transaction on Biomedical Engineering，2011，58(1)：121-131.

[10]Cai Haoyu，Ma Jiaxin，Shi Lichen，et al.A novel method for EOG features extraction from the forehead[C]//Proceedings of 33 rd annual International Conference of the IEEE Engineering in Medicine and Biology Society.Boston：IEEE，2011：3075-3078.

[11]Ma Jiaxin，Shi Lichen，Lu Bao-Liang.Vigilance Estimation by Using Electrooculographic Features[C]//Proceedings of 32 nd annual International Conference of the IEEE Engineering in Medicine and Biology Society.Buenos Aires：IEEE，2010：6591-6594.

[12]马家昕.基于眼电信号的警觉度估计模型研究[D].上海：上海交通大学，2010.

[13]杨建国.小波分析及其工程应用[M].北京：机械工业出版社，2005：63-74.

[14]Shi Lichen， Lu Baoliang. Off-line and on-line vigilance estimation based on linear dynamical system and manifold learning[C]//Proceedings of 32 nd annual International Conference of the IEEE Engineering in Medicine and Biology Society.Buenos Aires：IEEE，2010：6587-6590.