基于Fluent计算的火箭离轨姿态运动仿真与分析

关 宏 徐世杰

北京航空航天大学宇航学院，北京 100191



基于Fluent计算的火箭离轨姿态运动仿真与分析

关 宏 徐世杰

北京航空航天大学宇航学院，北京 100191

在航天器姿态运动分析中常遇到液体的流动、晃动及流/固耦合等问题，针对这类问题建立精确的数学模型是很困难的，通常需要利用数值计算和仿真手段进行分析。利用用户互动功能(UDF)，引入自定义的变量源函数，应用Fluent对运载火箭离轨姿态控制进行剩余燃料的流场数据分析。通过在流体运动方程中加入相关的牵连运动，得到在轨运行状态下贮箱内剩余液体的运动参数和对贮箱的干扰力矩，为运载火箭系统的姿态运动分析和仿真提供运算参数，使得流场的变化与运载火箭的姿态运动相关联，分析各个时刻流场运动状态对箭体姿态的影响。

Fluent;离轨;剩余液体;用户互动功能(UDF)

随着运载火箭技术的进步，使用液体推进剂的火箭已经成为航天器的主要运载工具。一些一次性使用的运载火箭和重复使用的航天飞行器，在主发动机关机后，不可用推进剂、安全储备、以及飞行混合比偏差所引起的剩余推进剂都将存留在贮箱里。这些残存的液体燃料在贮箱里的运动将会影响到运载火箭的姿态运动，甚至引起火箭姿态失稳。因此对贮箱里残存液体的运动分析和计算是十分必要的。实际工程中，运载火箭在分离后的回收过程中常遇到剩余液体晃动产生的问题。一般是将剩余液体的运动作为对火箭的干扰来处理，根据剩余液体不同的分布规律，采用偏微分方程描述其运动变化规律[1-2]，并作为姿态运动的流体分析干扰模型。但实际上，当残留液体体积远小于贮箱容积时，此方法难以反映贮箱-液体系统参数的瞬态分布特征，如果对贮箱和液体建立完整的动态数学模型，则存在建模困难、计算量大的问题，而且往往不能反映符合实际的参数分布特征。

目前，随着计算流体力学、分布式仿真技术的发展[3]，利用成熟的CFD仿真软件Fluent，对工程中常遇到的具有非定常分布模型的流场能够有效地进行计算，并且其建模简单、计算精度和可靠性都很高，在工程预研、仿真验证中得到了广泛的应用。Fluent软件具有很多优点，但还存在一定的局限性：一方面，仅靠流场仿真无法揭示航天器姿态运动和贮箱内流体运动的相互作用；另一方面，需要将Fluent加载到其他系统仿真软件中，若接口设计不当或网络连接不稳定将会影响仿真效率[4]。

本文根据Fluent软件本身的特点，利用其用户互动功能(UDF)[4]，通过系统参数的实时同步传输，使姿态动力学与运动学模块能够实时地影响Fluent计算参数，从而建立了研究分布参数的闭环控制仿真平台，为含有流体运动的姿态运动仿真提供新的途径。通过利用这种仿真手段，本文对某运载火箭离轨前的姿态稳定控制进行了数值计算与仿真，验证了该方法的可用性和有效性，分析了含有剩余燃料的情况下箭体离轨姿态的变化规律。

1 仿真系统的建立

本文选择某运载火箭末级推进器为研究对象，在完成轨道任务后氧化剂与燃料贮箱内均剩余少量推进剂，体积远小于贮箱容积。离轨过程中由于姿态调整以及箭体自旋运动，液体的分布难以确知，运动存在不可控因素，故采用Fluent流场模型对贮箱内液体进行仿真，同时通过UDF功能实现箭体姿态与液体运动的闭环仿真。

此处需要说明的是当箭体与液体作为整体系统看待时，不受外界干扰力矩作用，但是为了分析流体运动对箭体姿态的影响，需要将箭体与液体作为两个子系统，以分析其相互作用。

1.1 箭体系统动力学分析

首先以箭体系统作为研究对象，其转动惯量沿自旋轴对称，箭体本体坐标系Sb定义如图1所示，坐标原点Ob在箭体质心，Xb轴沿本体纵向对称轴方向，Yb轴沿箭体纵切面向上，Zb轴按右手法则定义。

图1 箭体本体坐标系定义

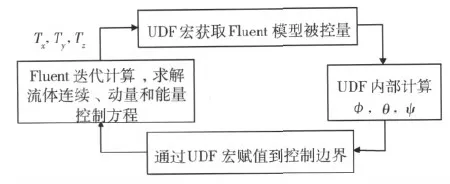
定义系统惯量主轴沿坐标轴方向：绕横轴的转动惯量为Iy，Iz，且Iy=Iz，绕纵轴(自旋轴)的转动惯量为Ix，且Ix

(1)

其中ωx,ωy,ωz分别为绕Xb,Yb,Zb轴的角速度。

方程左侧的Tx,Ty,Tz为箭体系统受到的外干扰力矩，本文即为剩余液体对箭体的作用力矩。

由式(1)以及轴对称刚体运动的特性可知：

1)刚体自旋轴Xb绕角动量H的圆锥运动称为空间章动，其空间章动速率Ω=H/It；

2)章动角γ为动量矩H与自旋轴之间的夹角，满足关系式cosγ=Ixωx/H；

图2 本体锥和空间锥

定义轨道参考系S系，与t=0时刻的本体系重合，x轴轨道切向，y轴沿t=0时刻箭体纵切面向上，z轴按右手法则定义。定义空间章动参考系S′系，坐标原点在航天器质心，x′轴沿本体纵向对称轴方向，y′轴沿章动角速度Ω在本体系的投影方向，t=0时刻箭体纵切面向上，随空间锥运动，z′轴按右手法则定义。在t=0时刻，此3坐标系重合。运动Δt时刻后，y轴在空间指向不变，y′轴运动α角，Yb轴运动到β角位置，α=∫ΔtΩdt为箭体空间章动运动角度，β=∫Δtωxdt为箭体自旋运动角度。即

1.2 液体子系统运动

得到箭体空间运动规律，再考虑液体系统的相应晃动影响。

液体子系统在微重力环境下运动，受扰动后不能断定其确切位置，液气界面稳定性差。一旦航天器进行姿态控制(起旋至稳定旋转)，剩余液体产生的扰动就会影响到姿态控制的精度，破坏航天器的运动稳定性。又因为液体运动规律不易简化，如不能准确仿真其运动状态，便无法找到适当的控制策略，会对回收造成恶劣的影响[6]。

本文流场模型选择图2中S′系为参考系，该参考系随箭体在空间不断运动，始终保证液体受空间锥离心加速度方向在y′轴上，网格坐标系原点为箭体质心位置，便于对Fluent定义相对加速度以及对质心求作用力矩。

基于质量守恒定律、动量定理、能量守恒定律、热力学定律以及流体的本身物性，在流体力学中存在一组制约流体运动的基本方程组，对于黏性不可压缩流体，满足：

(2)

其中，ρ为流体密度，v为流体相对运动速度，ρ=const，div(P)表示单位体积上应力张量的散度，f1为单位质量上的质量力分布函数。

从动量定理出发，任取一体积τ的流体，它的边界为A，其中流体动量的变化率等于作用于该体积上的质量力和面力之和。以f1表示作用在单位质量上的质量力分布函数，pn为作用在单位面积上的面力分布函数，则作用在τ上和A上的总质量力和面力为∫τρfδτ及∫SpnδA，而体积τ内的动量是∫τρvδτ，于是动量定理写成

(3)

由于∫ApnδA=∫τdiv(P)δτ，故得到式(2)中右侧第2项，又ρf1表示单位体积上的质量力。根据相对运动学原理，流体运动方程将写成：

(4)

在原有的流体运动方程中，流场网格模型可以计算出式(4)中的ar，即流体相对于S′系的相对加速度。但是要考虑与箭体运动的耦合运动，就需要补充由于旋转相对运动产生的惯性牵连加速度ae，以及柯氏加速度2(ω×vr)。本文采用S′系作为流场仿真的参考系，其本身就具有相对本体系旋转的相对运动，因此只需要考虑牵连运动，即此处ae。

如前节中指出箭体上各点相对于角动量H方向的向心加速度a=Ω2r，此处的ae=a。通过对箭体的姿态运动学求解，得到各个时刻的相对姿态角、姿态角速度，根据式(1)以及轴对称刚体运动的特性，即可通过瞬时姿态信息，解得空间章动速率Ω、章动角γ，通过三角函数关系便可轻松的得到各点到角动量H的距离r。由此得到需要嵌入到网格计算模型中的自定义加速度a。

1.3 Fluent-UDF接口的设计

为了解决流场模型与箭体姿态运动模型数据交换问题，在保证流场模型和姿态运动模型实时同步运行的前提下，数据准确交换，提出使用Fluent-UDF数据交换接口实现交互仿真。UDF与Fluent数据交互流程如图3所示。

图3 使用UFD的流体模型与姿态运动模型交互示意图

首先，根据流体网格中的初始化边界条件(其中包括了对流场加速度a的初始化定义)，进行1个步长的网格计算。得到这一步中网格内剩余液体对箭体的干扰力矩Tx，Ty和Tz。下面就进入到UDF程序计算中：

第1步：由Fluent流场模型解决流体运动的分布计算问题，根据流体对箭体(贮箱)的作用情况，定义UDF程序的入口：液体子系统输出对模型壁面的作用力、作用力矩；通过流场模型得到剩余液体对于箭体系统的干扰Tx，Ty和Tz，即为UDF程序的调用入口参数；

第2步：当UDF从入口处读出Tx，Ty和Tz后，再根据UDF程序中编写的姿态控制方程，计算包括了仿真对象的姿态动力学与运动学方程的姿态运动状况；

第3步：仍然是在UDF程序包中，调用加速度计算和转换程序。根据相对作用原理，得到流场各点的下一个时刻的牵连加速度a1，通过UDF输出接口赋值到Fluent网格计算环境中。

此时，完成一个步长的箭体与液体系统的交互仿真计算，根据此时刻的网格场内加速度a1，进行下一个步长的网格参数计算，回到第1步。其中主要涉及的UDF源文件定义如下：

对应第1步：源文件1：

DEFINE_INIT()

{定义箭体姿态运动初始条件}

对应第2步：源文件2：

DEFINE_ADJUST()

{加载所需参数，包括作用力矩，姿态运动信息，姿态运动变化率，中间参数；

判断循环条件；

姿态动力学与运动学运动方程计算、叠加；

返回姿态运动变化参数，姿态运动信息；}

对应第3步，源文件3：

DEFINE_SOURCE()

{Real 加载所需参数；

调用加速度定义函数；

Return 加速度；}

仿真开始后，当网格计算一步长时，源文件1运行，将姿态运动方程的初始化条件Tx，Ty和Tz载入；之后，源文件2运行，计算姿态动力学和运动学方程，得出这一步箭体的姿态运动状态；最后，源文件3调用上一步得到的姿态运动状态参数，计算流场模型需要加载惯性加速度。每一步UDF计算开始时，都需要从网格载入上次循环时在流体系统计算中得到的作用力矩Tx，Ty和Tz，通过上述3个源文件再得到下一步的网格场加速度。将下一个时刻的网格场加速度a1输出到网格边界条件中，进行下一步网格计算。循环这一过程，就实现了Fluent计算和姿态动力学与运动学计算之间的实时同步数据传输过程。

2 仿真结果与分析

图4 液体晃动对航天器的作用力矩

由于液体的振动以及章动运动，S′系中y′轴方向上的作用力矩振荡上升，始终在其正方向上。即，在Fluent仿真的网格计算模型中，通过自定义源函数加载的惯性加速度始终指向离心方向，符合客观规律。通过Fluent流体系统仿真模型还可以看到运动过程中各个时间点的流场分布情况，如图5。

图5 不同时刻流场分布图

随着贮箱内的液体不断地向一侧壁面碰撞，产生对该侧的作用力。图7中左侧的贮箱离质心较远，这种碰撞作用力产生的力矩效果更加明显。右侧的贮箱内包含有坐标原点，液体因表面张力的作用环绕壁面流动，产生对壁面的剪应力，以及对质心的作用力矩。

图5中是根据时间顺序选择的3幅典型的流场分布图，其中左侧贮箱内，如果对照图5中各个状态下的流场分布情况，便可轻易地分析图4(a)中的作用力矩变化的原因。左侧贮箱的液体越来越多地与贮箱的一侧碰撞，使碰撞力的作用增大；右侧贮箱的液体分布逐渐均匀，与贮箱壁面的接触面积增大，摩擦力矩也随之增大。因此，图4(a)中的力矩变化刚好与图5中的流场分布变化相吻合。

原来罗漠与任何人都是一样的，他的独特，他的深情，都只为一人而已。他的爱那么忠诚，经得起各种各样的考验，她其实是满意的，可是她忍不住流了一路的眼泪。

在这种作用下，箭体的姿态运动受到的干扰应当是越来越大的，下面再对箭体系统进行分析。图4(a)中将S′系中的作用力矩投影到本体系Sb中，其方向与本体系当时的相对位置有关。箭体系统受到的液体干扰力矩就是图4(b)中的作用力矩。根据本文第1.1节中箭体动力学方程，得到在剩余液体干扰下箭体的姿态运动状态，如图6所示。

图6 液体干扰作用下的箭体自旋轴空间指向

从图6分析整个系统的运动状态：在仿真时间内，箭体系统章动逐渐增加，因此旋转离心作用增大，必然导致液体相对于箭体运动加强。根据液体运动对质心的力矩分析可知，液体干扰作用力矩也应当是逐渐增强的，与Fluent网格模型的仿真结果一致。并且随着箭体运动稳定性的恶化，绕最小惯量轴(自旋轴Xb轴)的自旋运动最终转化为绕最大惯量轴(Yb轴或Zb轴)的不规则旋转运动，因而箭体运动发散后在S′系中y′轴方向上的作用力矩出现下降并且幅值也产生不规则的变化。

本文选择的仿真方法不仅可以测得流场与箭体的相互影响参数，通过编写合理的UDF程序，还可以选择模型中任意位置作为观测点，测量其在流场中所受的作用力矩，或者对流场内的压强、温度、过载进行中间控制，通过适当的控制程序在相应时间修改这些参数。并且，也可以将包含控制判断算法的程序以UDF程序的形式添加到闭环系统中，形成含有实时控制系统的姿态耦合运动仿真模型。

这种方法的优点在于可以直观形象地观察到仿真各个时刻系统的变化和状态，便于分析影响姿态运动的各种因素。同时，这种选择离心运动坐标系为仿真参考系的方法可以简化箭体姿态运动对液体影响的描述，通过简单的投影关系就可以得到清晰、解耦的作用关系。

由此可知，Fluent-UDF技术适用于更复杂的分布参数系统，可以推广到更复杂的包含流体计算的系统控制模型中。

3 结论

[1] S.Dutta, M.K.Laha.Analysis of the Small Amplitude Sloshing of a Liquid in a Rigid Container of Arbitrary Shape Using a Low-order Boundary Element Method[J].International Journal for Numberical Methods in Engineering, 2000, 1(47): 1633-1648.

[2] 王照林, 李磊.航天器内部液体晃动对交会对接动力学与控制的影响[J].航天控制, 1991,(2): 24-32.(WANG Zhaolin, LI Lei.Effect on Dynamics and Control of Rendezvous and Docking due to Liquid Sloshing Internal to Spacecraft[J].Aerospace Control, 1991, (2): 24-32.)

[3] 耿浩, 蒋志文.基于网格的分布式仿真技术[J].航天控制, 2004, 22 (6): 46-48.(GENG Hao, JIANG Zhiwen.Distributed Simulation Technology Based on the Grid[J].Aerospace Control, 2004,22 (6): 46-48.)

[4] 鲍文, 李伟鹏, 等.基于Fluent/Matlab接口的分布参数系统闭环控制仿真[J].北京:系统仿真学报, 2008, 20 (11):2851-2854.(BAO Wen, LEI Weipeng, et al.Close-loop Control Simulation Technology of Distributed Parameter System Based on FLUENT/MATLAB Interface[J].Journalof System Simulation, 2008,20 (11): 2851-2854.)

[5] 肖业伦.航天器飞行动力学原理[M].北京: 宇航出版社, 1995: 212-217.(XIAO YeLun.Theory of Spacecraft Dynamics[M].Chinese Astronautics Press, 1995: 212-217.)

[6] 廖少英.低重力或失重环境下剩余推进剂的管理和排放技术研究[J].上海航天, 1993, 5: 13-18,40.(LIAO Shaoying.Research of the Residual Propellant Dumping System under Micro-gravity[J].Aerospace Shanghai, 1993, 5: 13-18,40.)

《航天控制》杂志

□欢迎订阅 □欢迎刊登广告 □欢迎投稿

开本：大16开 双月刊 页码：96页 定价：20.00元(全年120元)

国内邮发代号：80-338 国外发行代号：BM4668

国内统一连续出版物号：CN11-1989/V 国际标准连续出版物号： ISSN 1006-3242

编辑部地址：北京142信箱402分箱 邮政编码：100854

电话：(010) 68762264、68388585 E-mail: ht12@httx.com.cn

网址：http://htkz.chinajournal.net.cn

The Analysis and Simulation of Attitude Motion for a De-orbit Rocket Based on Fluent Flow Field Calculation

GUAN Hong XU Shijie

School of Astronautics, Beihang University, Beijing 100191, China

Duetotheattitudemotionanalysisofaspacecraft,thefluxionandsloshingofliquidarefrequentlyencountered.Sinceitisdifficulttoestablishaprecisemathematicalmodelforsuchissues,researchersprefertousenumericalcalculationandsimulationforanalysis.Inthispaper,theUDFisusedtointroducetheuserdefinedvariablefunctionandtherocketde-orbitcontrolwithflowfieldsimulationofresidualfuelbasedonfluentistokenforexampletoanalyze.Byaddingtransportmotiontothefluidmotionequations,theparametersanddisturbingtorqueofflueundertheon-orbit-statecanbeobtained.Theoperationparametersofattitudeanalysisandsimulationforlaunchvehiclesystemareprovidedsothatthechangesinflowandtheattitudemotionofthelaunchvehiclearecorrelated.

Fluent;De-orbit;Residualfuel;User-definefunction(UDF)

2011-08-16

关 宏(1985-)，女，北京人，博士研究生，主要研究方向为航天飞行器动力学与控制；徐世杰(1951-)，男，吉林人，教授，博士生导师，主要研究方向为航天飞行器动力学与控制。

V525

A

1006-3242(2012)03-0093-06