基于模态振型的简支梁损伤识别

宫 振，肖宗萍，杨 斌

（1.云南文山天成房地产开发有限公司，文山663000；2.云南省文山州建筑工程有限公司，文山663000；3.建研地基基础工程有限责任公司，北京100013）

0 引 言

工程结构在服役期间受到设计荷载和其所处的环境激励的影响，不可避免的会出现各种各样的损伤.损伤的结构在其损伤位置处刚度降低，受力截面面积减小，产生应力集中现象，如不及时进行修复，结构形式发生改变，承载能力急剧下降，会对结构的使用寿命产生极大的影响.因此，结构损伤检测，是结构诊断、评估和加固的前提，结构损伤识别，主要有局部法和整体法［1］.

传统的损伤识别方法有目测法、发射光谱法、染色法、回弹法、声发射法、渗漏试验法、射线法、脉冲回波法、磁粒子法、磁扰动法、涡流法等等［2］.基于模态的结构损伤识别技术是近几十年来逐步发展起来的一门新兴学科，从20世纪90年代至今，中外学者提出了许多损伤识别的方法，如动力指纹（频率、振型、应变模态、模态柔度矩阵曲率等）分析法、模型修正与系统识别法、神经网络法和遗传算法，并通过实例验证方法的可行性和适用范围［3］

1 理论基础

结构的模态参数（频率、振型等）是结构物理参数（质量、刚度等）的函数，通过模态参数的改变来识别物理参数的改变，即基于模态的损伤识别的原理.Pandy和Biswas［4］利用结构损伤前后模态振型曲率的差值提出了振型曲率法.由材料力学得知梁截面的曲率公式为

其中v″、M、E、I分别为梁截面相对应的曲率、弯矩、弹性模量和截面惯性矩.由上式可以看出，当结构某处损伤产生刚度的变化时，必然引起此处曲率的改变，因此可以通过曲率的改变来确定损伤的位置，曲率的改变量来确定损伤的程度.

结构的振型曲率是振型的二阶导数，当结构是由n个单元组成的有限自由度体系时，其振型曲率可以通过中央差分公式求得.

其中i为节点的位置，j为模态振型的阶数，φi＋1，φi－1，j为相邻两节点的振幅，h为相邻两节点的距离.结构损伤前后的振型幅值分别为φi，j、φdi，j，幅值变化量Δφi，j＝φdi，j－φi，j，即结构的振型变化曲率值为

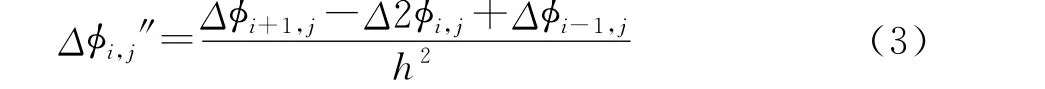
袁向荣［5］对结构振型识别损伤进行了研究，对比分析了振型差和振型曲率差两种损伤标示量对结构损伤识别的敏感度；郭国会［6］利用振型的变化对一框架结构进行了损伤识别，取得了良好的效果.

2 简支梁算例

ANSYS软件是集结构动力学、热力学、流体力学、电磁学、声学于一体的大型通用有限元分析软件.其中结构动力学包括模态分析、谐响应分析、瞬态力学分析和谱分析，模态分析主要用于确定结构和机器部件的振动特征即模态参数（频率、振型、阻尼等）.

为了研究损伤对简支梁结构模态振型的影响，建立有限元模型如图1所示.

图1 简支梁有限元模型

简支梁全长1m，分为17个节点，16个单元，单元采用Beam 2Delastic 3.单元截面面积1.415×10－3m2，截面惯性矩Ix＝2.45×10－6，材料为各向同性，密度为7850m2，弹性模量E＝2.1×1011，泊松比0.3.假设单元受到损伤时，仅仅是弹性模量发生变化，其他不变，结构受到两种情况的损伤，轻度损伤弹性模量降低1／3，重度损伤弹性模量降低1／2.对结构进行模态分析，采用block lanczos算法.对表1所示五种工况进行模态分析.

表1 模态分析不同工况

对表1所示前四种工况下的简支梁模型进行模态分析，对1阶振型求曲率差，绘制结果如图2～5所示.

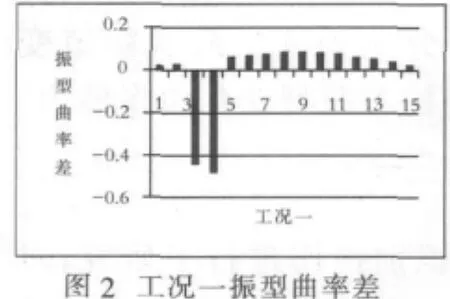
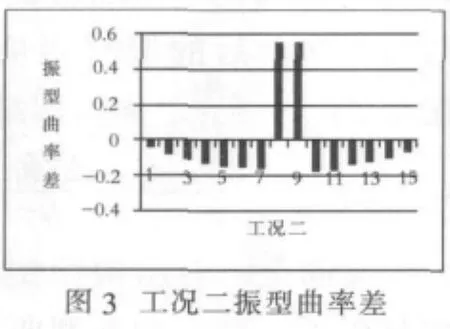
由图2可以看出，在3、4直方有明显的向下突变，而其他直方皆为正值，判定单元4发生了损伤，同理可以得出其他三种工况的损伤单元位置.由于在进行振型曲率求解的过程中舍弃了第一个点，故判定数值较大的直方为损伤的单元.由图2～图5可以看出，1阶振型曲率差对简支梁结构的一处和多处损伤都有较好的识别效果.

利用2阶和3阶模态振型的曲率差，对结构工况一的情况进行损伤识别，绘制结果如图6和图7所示.

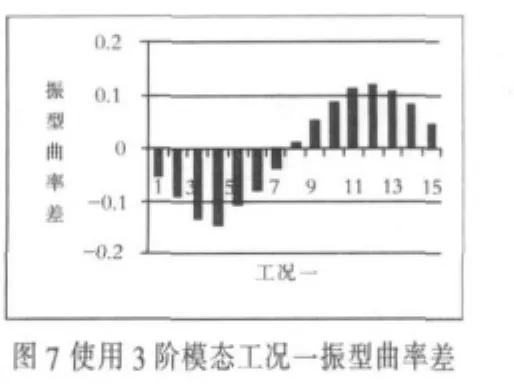
由图中可以看出，损伤单元处的突起并不明显，无法判定损伤单元的位置.因此，利用高阶振型曲率差对简支梁结构的识别效果并不显著.

下面利用1阶振型曲率差对结构在单元4、9、15处发生不同程度损伤的工况下进行对比，对比图如图8所示.

图8 工况四、五振型曲率差对比

由图中可以看出，随着单元损伤程度的加深，振型曲率差图形的突变也增大，因此，利用振型曲率差对简支梁结构的损伤程度也有较好的定性识别效果.

3 结 论

文章对基于振型曲率差的结构损伤识别方法对简支梁进行了损伤位置和程度的识别，由上述分析可以得出结论：

（1）简支梁结构的1阶振型曲率差对结构的一处和多处损伤位置都有较好的识别效果.

（2）高阶振型对简支梁结构的识别效果并不显著，甚至无法进行识别.

（3）对简支梁结构的损伤识别程度，利用振型曲率差，只能进行定性的比较.

［1］ 李宏男，李东生.土木工程结构安全性评估、健康监测及诊断述评［J］.地震工程与工程振动，2002，22（3）：82－90.

［2］ 宗 超.建筑物结构损伤诊断技术现状与展望［J］.价值工程，2010，29（27）：120－121.

［3］ 郑栋梁，李中负，华宏星.结构早期损伤识别技术的现状和发展趋势［J］.振动与冲击，2002，21，（2）：1－4.

［4］ Pandy A k，Biswas M，Samman M M.Damage Detection from Changes in Curvature Mode Shape［J］.Joural of Sound Vibration，1991，145（2）：321－332.

［5］ 袁向荣.梁的破损对频率振型及振型曲率的影响［J］.振动、测试与诊断，199，14（2）：40－44.

［6］ 郭国会，范培生，亿伟进.基于振型变化的框架结构破损评估［J］.重庆建筑大学学报，1998，20（6）：79－82.