考虑盾尾注浆隆起的盾构掘进地面位移预测

林存刚，吴世明，张忠苗，刘冠水，李宗梁

（1.浙江大学a.软弱土与环境土工教育部重点实验室；b.岩土工程研究所，杭州310058；2.杭州运河隧道有限公司，杭州310002；3.杭州庆春路过江隧道有限公司，杭州310002）

隧道施工不可避免地扰动周围地层，进而对邻近建（构）筑物造成影响。研究隧道施工引起的土体位移规律，对隧道施工引起的地层位移的准确预估，对于减轻隧道施工带来的环境危害十分重要。为此，众多学者展开了深入的研究，研究方法以经验公式、解析法、数值模拟及模型试验为主。

土压平衡盾构法和泥水盾构法是目前软土地层最为先进的隧道施工技术。其以切口压力的精确控制，盾壳对土层的支护，同步注浆对建筑空隙的及时填充等先进技术，与之前工法相比，引起的地面沉降更小，甚至会引起地面隆起。之前学者对盾构掘进引起的地面位移研究［1－10］，集中在施工引起的地面沉降的计算，这主要是因为之前的工法因地层损失较大，地面以沉降为主，很少观测到隆起。而土压平衡盾构和泥水盾构掘进引发地面隆起的现象较为普遍，但对此的研究却很少。

本文通过3个盾构隧道工程实例地面位移的分析，探讨了盾构盾尾注浆引起的地面隆起的分布规律，对比分析了 Mindlin解［1－2］、Sagaseta法［3－4］、Verruijt－Booker 法［5］、Loganathan－Poulos 法［6］、Chi法［7］和Park法［8］6个解析／半解析公式及高斯公式预测盾构施工地面隆起的适用性，并结合工程实例给出了考虑注浆地面隆起后盾构掘进地面位移计算的修正 Peck公式［9］。

1 隧道施工地层位移的预测方法

以下公式采用统一坐标系统，x为盾构掘进方向，y为垂直于隧道轴线方向，z轴为地面隆陷方向；地面位移以隆起为正，沉降为负。所有公式均未考虑固结，认为土体不排水。

1.1 Peck公式

Peck［9］公式是目前工程实践中应用最为广泛的隧道施工横断面地面沉降预测公式之一，其表达式为：

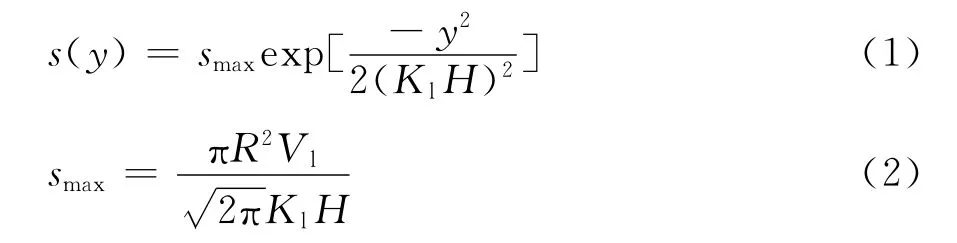
式中：s（y）为至隧道轴线水平距离y处地面沉降，m；smax为轴线位置地面沉降，m；y为至隧道轴线水平距离，m；H为隧道轴线埋深，m；Kl为地面沉降槽宽度参数（无量纲）；Vl为地层损失率，地面单位长度沉降槽面积与单位长度隧道开挖面积之比（无量纲）。

1.2 Mindlin解

Mindlin［1－2］推导出竖向和水平点荷载作用于弹性半无限空间内部时任意位置的附加应力及位移的表达式（式（3）、（4）），其计算模型如图1所示。

图1 Mindlin解示意图

图中，集中力作用点坐标（0，0，c）；R1＝

式中：x′、y′、z′为所求点在图2所示坐标系中位置，m；Pv、Ph为分别为竖向集中力与水平向集中力，kN；v为土体泊松比；G为土体剪切模量，kPa；c为集中力作用点深度，m；w1、w2为分别为Pv、Ph作用下（x′、y′、z′）位置竖向位移，m。

本文基于Mindlin解，积分推导盾尾同步注浆附加压力作用下引起的地面隆起。

计算做如下假定：1）土体为弹性半无限空间；2）盾构水平掘进；3）盾构外径2R，长L，轴线埋深H；4）同步注浆附加压力p沿盾尾圆周均匀分布，方向为圆周径向朝外，作用长度为盾尾以后一环管片宽度，m。

盾尾同步注浆附加压力引起的地面竖向位移计算模型见图2。切口位于x＝0位置，盾构轴线位于x轴正下方。

如图2所示，对于任一微元dA＝R·ds·dθ，其所受集中力为dp＝p·R·ds·dθ，其坐标系为x′－y′－z′，c＝H－R·sinθ。dp分解为水平分力dph＝p·R·cosθ·ds·dθ和竖直分力dpv＝p·R·sinθ·ds·dθ。

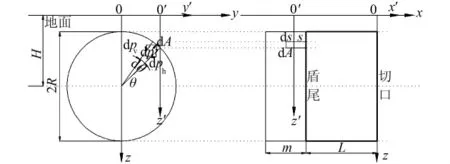
图2 Mindlin解积分示意图

坐标变换：

1）dph引起土体竖向位移：

代入式（4），得：

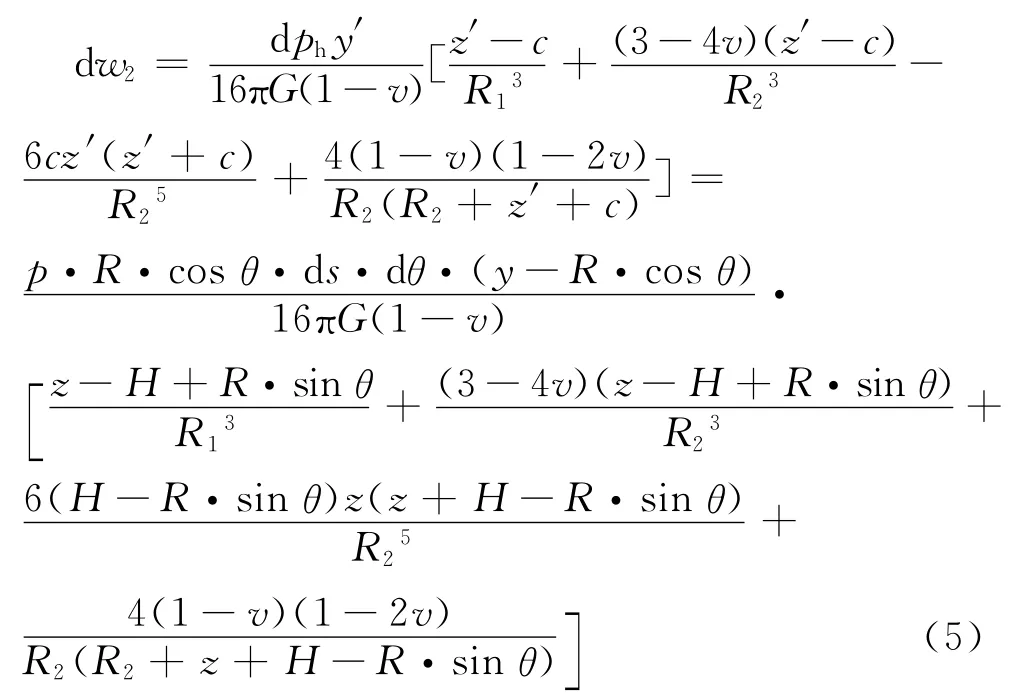
式中：

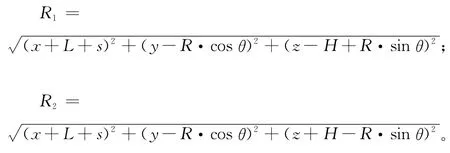
2）dpv引起土体竖向位移：

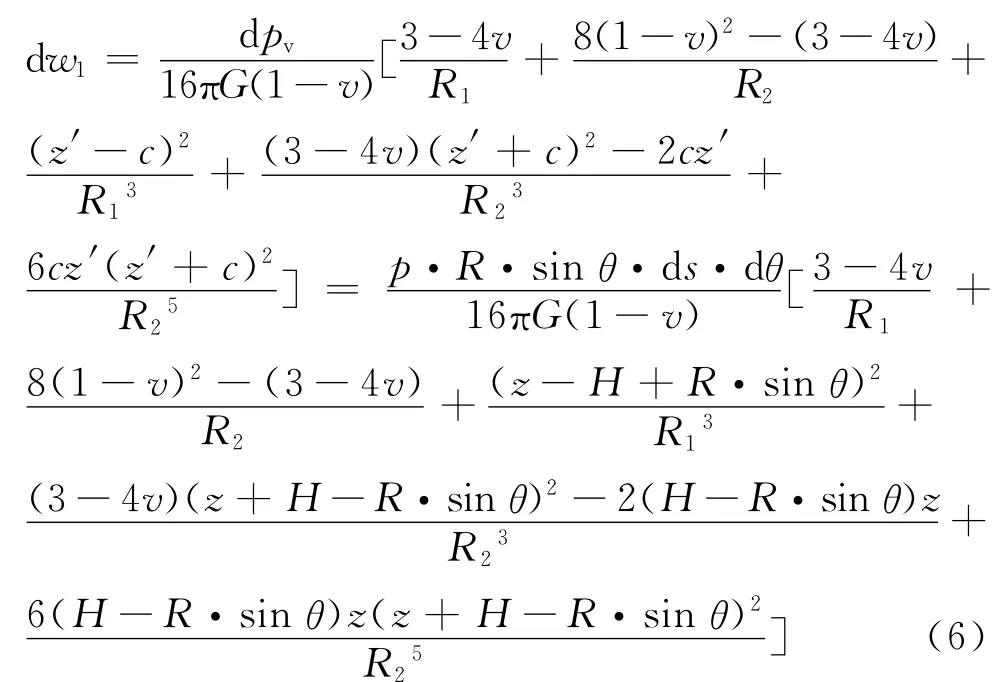
代入式（3），得R1、R2取值同式（5）。

盾尾同步注浆附加压力引起x－y－z坐标系中任意点（x，y，z）竖向位移wp：

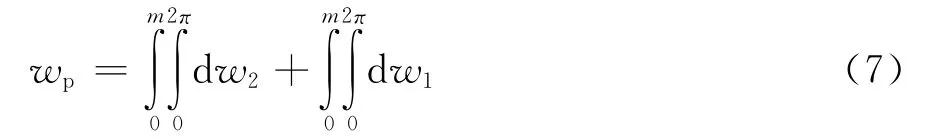
式（5）、（6）较复杂，进行双重积分难以得到其表达式，为此式（7）的计算采用6点Gauss－Legendre数值积分［11］。

1.3 Sagaseta法

Sagaseta［3－4］假定土体为线弹性半无限空间，不可压缩，引入流体力学中虚拟镜像技术，推导得出地层损失引起的地表位移解析式（8）。

1.4 Verruijt－Booker法

Verruijt［5］在Sagaseta基础之上，同时考虑地层损失及隧道椭圆化变形引起的地面位移，并扩展到可压缩性土层，其计算公式（不计隧道椭圆化变形项）：

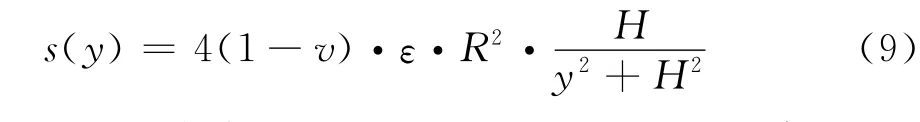
式中：ε为隧道周围土层的均匀径向收缩率，ε＝u0／R，u0为隧道周围土体朝向隧道中心的均匀径向位移。

ε与Vl可互相转化［11－13］：

1.5 Loganathan－Polus法

Verruijt法假定隧道周围地层损失均匀分布，Loganathan等［6］在此基础之上，认为地层损失沿隧道周边不均匀分布，给出基于间隙参数g的粘土地层中隧道施工引起的地面沉降表达式：

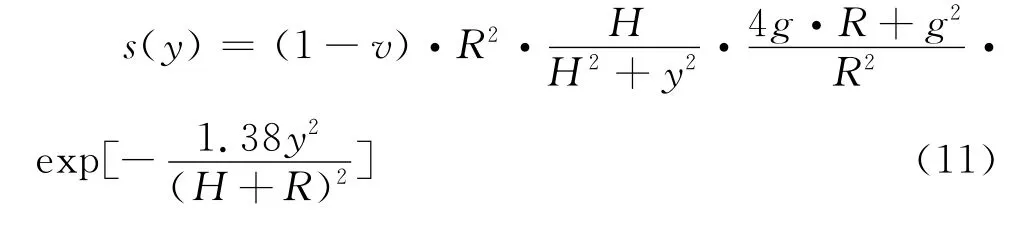
式中g为间隙参数。

g与Vl可互相转化［8］：

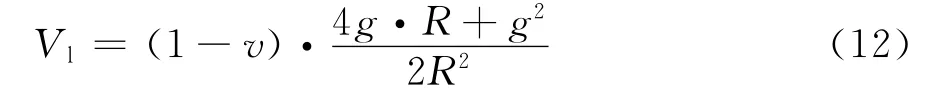
1.6 Chi法

Loganathan－Poulos公式针对粘土地层建立，Chi等［7］在此基础之上，引入地层沉降影响角β，将Loganathan－Poulos法拓展至砂土地层：

式中：β为地层沉降影响角，Chi等通过台北捷运系统隧道施工地面沉降反分析，得出粘土地层β约为45°，砂土地层β取值范围为30°～50°，平均为41°。

g与Vl的转化关系同式（12）。

1.7 Park法

Park［8］在 Verruijt ＆Booker基础之上，假定隧道周围土层4种位移边界条件，相应建立了4种地层沉降计算公式。

其中第2种边界位移条件下，地层沉降为式（14）。Park假定土体不排水，不可压缩。

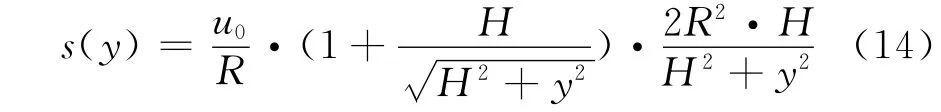
2 注浆地面隆起计算

前面所述7种地面位移计算理论，其中1.1，1.3～1.7均用于计算由于隧道开挖地层损失引起的地面沉降。

盾构软土地层掘进，经常发现由于同步注浆作用，地面出现上抬。笔者认为，同步注浆作用下的地面隆起，为浆体挤压隧道周围土层所致，是地层损失的反过程，因此其引起的地面位移同样可以用方法1.1，1.3～1.7预估。

对于Mindlin解，则是由同步注浆附加压力推算地面隆起形式。由于Mindlin解计算位移，与受力大小一一相关，受力改变，变形随之改变。但是隧道周围土层在同步注浆附加压力作用下外扩后，由于浆液填充了原来土层的位置，所以即使注浆附加压力消散，土层位移也无法回弹，因此，土层在同步注浆附加压力下的位移是逐渐累积的。而同步注浆附加压力的作用是间歇性的，作用持续时间也不定，因此很难由注浆附加压力计算出地面累积隆起值。在本文中，Mindlin解只是用来计算同步注浆附加压力下地面隆起位移曲线的形状，隆起量值应根据具体注浆量确定。

下面对3个盾构隧道工程实例进行分析。

2.1 杭州庆春路过江隧道工程

2.1.1 工程概况 杭州庆春路过江隧道南北方向垂直穿越钱塘江，盾构段总长3 532.442m，其中东线长1 765.478m，西线长1 766.924m。管片外径11.3m，内径10.3m，厚50cm，环宽2m。管片采用通用契型环，采用6标准块＋2邻接块＋1封顶块的分块形式，错缝拼装，纵环向采用高强螺栓连接。

盾构隧道采用2台泥水平衡盾构机从江南盾构工作井始发。盾构主机长L＝11.4m，重1 100t，外径2R＝11.65m。

盾构施工主要穿越粉砂夹粉土、淤泥质粉质粘土、粉质粘土、粉细砂和圆砾层。孔隙潜水赋存于场区浅部人工填土及其下部粉、砂性土层内，水位高，渗透性好。砂土、圆砾为承压水层，承压水位高，透水性强。

2.1.2 注浆所致地面隆起分析 杭州庆春路过江隧道泥水盾构掘进过程中，在盾尾脱离监测断面之后，受同步注浆的影响，地面经常观测到上抬。下面就典型断面D7和D5展开分析。

1）D7断面 D7断面位于东线隧道钱塘江江北大堤至盾构接收井之间。该断面隧道上覆土层为填土、砂质粉土、粉土夹淤泥质土、粉砂夹粉土，开挖面土层为粉砂夹粉土、淤泥质粉质粘土、粉质粘土、粘土；轴线埋深H＝24m，土体泊松比v＝0.28，剪切模量G＝10MPa。

图3为盾构切口位于不同位置时，D7断面轴线地面位移的变化曲线。图中，x表示监测断面与盾构切口的距离，监测断面位于切口前方时为正值。对应图3中x＝0m，x＝－11m位置横断面地面位移曲线见图4。

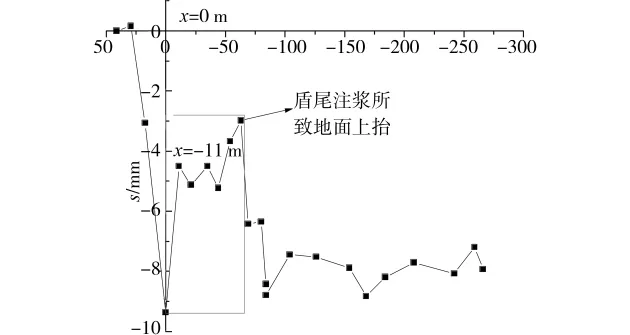
图3 D7轴线地面位移随盾构位置的变化曲线

图3可见，由于盾尾注浆作用，地面出现上抬。

图4可见，x＝－11m位置相对于x＝0m时，地面因注浆产生隆起。横断面地面隆起曲线为（S1S0）。

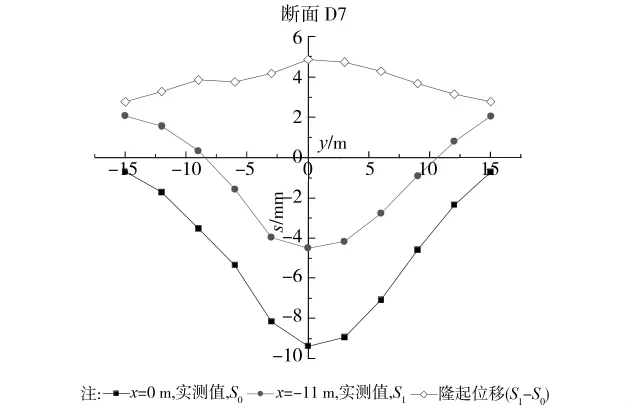
图4 D7断面x＝0m，－11m处横断面地面位移

对隆起曲线用高斯公式进行拟合，以确定曲线隆起宽度范围及隆起量2个参数，然后采用其他6种方法加以计算。拟合及计算结果见图5及表1。

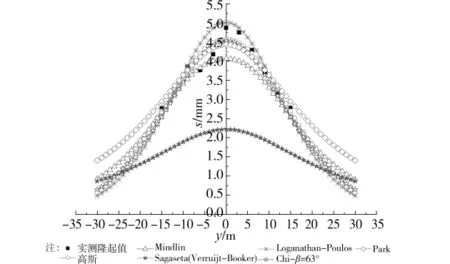
图5 D7断面横断面隆起位移实测值及拟合、计算值

图5及表1可见，盾尾注浆引起的横断面地面隆起，基本符合高斯分布；在高斯曲线拟合近似确定实际注浆地层补偿率后，其他6种方法均以此注浆补偿率进行计算，计算结果可见：

（1）Mindlin解所确定的地面隆起曲线，其注浆隆起宽度参数为0.689，略大于实测隆起曲线的注浆隆起宽度参数0.609，但其计算隆起量，在距离轴线10m距离之内，明显小于实测值。

（2）Sagaseta法和 Verruijt－Booker法计算结果一致。这2种计算方法高估了注浆隆起宽度参数，从而使得距轴线15m范围内的计算隆起量远远小于实测值。

（3）Loganathan－Polous法计算结果与实测值基本吻合，其计算曲线宽度参数与实测值相差不大。

（4）β取63°时，Chi法计算结果与实测值基本吻合，其计算曲线宽度参数与实测曲线比较接近。

（5）Park法计算结果在距隧道轴线15m范围内基本接近实测值，但是其宽度参数较实测值偏大，离隧道轴线较远（大于15m）时，其计算结果将远大于实际情况。

综上，对于D7断面，其横断面注浆隆起基本符合高斯分布；Loganathan－Polous法和 Chi法（β＝63°）计算结果与实测值比较接近，基本预测了地面隆起量和隆起宽度范围。

表1 横断面地面隆起拟合及计算参数

2）D5断面 D5断面位于东线隧道钱塘江江北大堤至盾构接收井之间。该断面土层情况同D7，隧道轴线埋深24m。

图6为D5断面轴线地面位移随盾构切口位置的变化曲线，图7为对应x＝－14m，x＝－35m位置横断面地面位移曲线。

图6、7可见，盾尾脱离后，由于同步注浆作用，地面上抬，使得距隧道轴线10m之外地面出现隆起。

对于实测注浆隆起的Gaussian曲线拟合及其他6种方法的计算结果见图8及表1。

图8及表1可见，盾尾注浆引起的D5横断面地面隆起，符合高斯分布；其他6种计算方法：

（1）Mindlin解计算所得地面隆起曲线，其隆起宽度参数大于实测值，距轴线10m范围内计算值较实测偏小。

（2）Sagaseta法和 Verruijt－Booker法计算结果一致。这两种计算方法过高估算了注浆隆起宽度参数，从而使得距轴线15m范围内的计算隆起量远远小于实测值。

图6 D5轴线地面位移随盾构位置的变化曲线

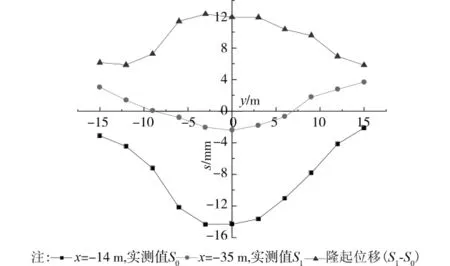
图7 D5断面x＝－14m，－35m处横断面地面位移

图8 D5断面横断面隆起位移实测值及拟合、计算值

（3）Loganathan－Polous法计算结果，其隆起宽度参数略高于与实测值，距轴线10m范围内计算沉降量较实测略低，但仍可以基本反映出注浆隆起量和隆起宽度。

（4）β取54°时，Chi法计算结果与实测值基本吻合，其计算曲线宽度参数与实测曲线比较接近。

（5）Park法计算结果在距隧道轴线15m范围内小于实测值，其宽度参数较实测值偏大，离隧道轴线较远（大于15m）时，其计算结果将远大于实际情况。

综上，对于D5断面，其横断面注浆隆起基本符合高斯分布；Chi法（β＝54°）计算结果与实测值最为接近，其次为Loganathan－Polous法。

可见，在杭州庆春路过江隧道泥水盾构施工过程中，由同步注浆引起的地面隆起基本符合高斯分布，其隆起宽度参数约为地层损失沉降槽宽度参数的1.62～2.14倍；Mindlin解、Sagaseta法、Verruijt－Booker法及Park法计算所得隆起曲线与实测值差别较大，无法预测实际注浆隆起的宽度范围和隆起量；而Loganathan－Poulos法及Chi法（β介于54°～63°之间时）计算隆起曲线与实测基本吻合。

2.2 南京长江隧道工程

2.2.1 工程概况 南京长江隧道位于南京长江大桥与三桥之间，盾构隧道段采用双管单层的结构形式，隧道分东西两线。管片环外径14.5m，内径13.3m，环宽2m。盾构隧道段采用泥水盾构掘进，盾构长约14.3m，外径14.93m［15］。

隧道穿越场地为长江冲积平原区，主要为堤外滩地、堤内高漫滩、堤内低漫滩，长江水域及江心洲。盾构始发段主要穿越第四系和白垩系地层，隧道场地通过部位不存在断裂或破碎带。上覆地层和盾构穿越地层为第四系全新统冲淤积流塑淤泥质粉质粘土、淤泥质粉质粘土夹粉土、粉土等［15］。

2.2.2 盾尾注浆引起的地面隆起分析 以下分析断面，均位于盾构始发段，地面位移实测数据均引自文献［15］。盾构开挖半径为7.465m，土体泊松比为0.46。

西线始发段地面，监测断面RK3＋662、RK3＋678、RK3＋710、RK3＋735、RK3＋668、RK3＋672、RK3＋685、RK3＋690、RK3＋695、RK3＋700、RK3＋715、RK3＋720、RK3＋725、RK3＋730，共计14个断面，均发现，盾尾离开监测断面后，由于同步注浆作用，地面出现不同程度上抬。现对典型断面RK3＋678和RK3＋735进行分析。

1）西线隧道RK3＋678断面

西线RK3＋678断面隧道轴线埋深H＝16.85m。

图9为盾构切口位于不同位置时，RK3＋678轴线地面位移变化曲线。对应图9中x＝－13.4m，x＝－21.4m位置横断面地面位移曲线见图10。

图9 RK3＋678轴线地面位移随盾构位置的变化曲线

图9、10可见，盾尾脱离RK3＋678断面后，由于同步注浆作用，地面出现上抬。对于隆起位移用高斯曲线拟合及其他公式计算结果见图11及表1。

图11可见，Gaussian公式和Chi法（β＝20°）与实测注浆隆起基本吻合，而其他方法计算结果与实测有较大出入。

图10 RK3＋678断面x＝－13.4m，－21.4m处横断面地面位移

图11 RK3＋678断面横断面隆起位移实测值及拟合、计算值

2）西线隧道RK3＋735断面

西线RK3＋735断面隧道轴线埋深H＝19.75m。

图12为盾构切口位于不同位置时，RK3＋678轴线地面位移变化曲线。对应图12中x＝－10.4m，x＝－16.4m位置横断面地面位移曲线见图13。

12 RK3＋735轴线地面位移随盾构位置的变化曲线

图12 、13可见，盾尾脱离RK3＋735断面之后，由于同步注浆作用，地面土体上抬。注浆所致地面隆起高斯公式及其他方法计算结果见图14及表1。

图13 RK3＋735断面x＝－10.4m，－16.4m处横断面地面位移

图14 及表1可见，Gaussian公式和Chi法（β＝31°）计算所得隆起曲线与实测比较接近，而其他方法均因过高估计了隆起宽度参数而使得计算曲线与实际偏差较大。

4 RK3＋735断面横断面隆起位移实测值及拟合、计算值

综上，对于南京长江隧道泥水盾构掘进盾尾注浆引起的地面隆起，Gaussian公式和Chi法（β＝20°～31°）计算结果与实测值基本吻合；而其他方法计算所得曲线宽度参数远大于实测值，与实际出入较大。注浆隆起宽度参数是地层损失沉降槽宽度参数的1.07～1.17倍。

2.3 Madrid地铁延伸段

2.3.1 工程概况［13－14］马德里地铁延伸段工程从1995年9月开工，1999年2月竣工，共完成隧道里程38km，耗资4 400万美元。隧道上覆及穿越土层主要为填土、粘土、粉质粘土、砂土、粉质粘土。隧道全部由土压平衡盾构掘进完成，隧道外径9.4m，盾构长约10.8m。土体泊松比v＝0.3。

2.3.2 盾尾注浆地面隆起分析 Melis等［13－14］对隧道沿线5个断面的地面位移进行了分析，本文分析引用其所给实测数据。

第5断面，即里程8＋770处，盾构掘进引起了地面隆起，分析如下：

里程8＋770断面，隧道轴线埋深H＝19.9m。轴线地面位移随切口位置的变化曲线见图15，其x＝－40m对应的横断面地面位移见图16。

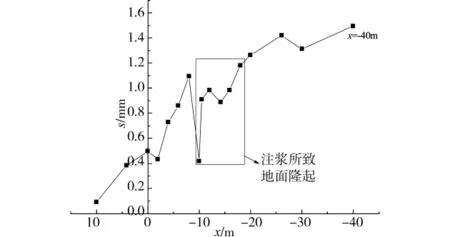
图15 8＋770断面地面位移随盾构位置的变化曲线

图16 8＋770断面x＝－40m处横断面地面位移

图15 可见，盾尾脱离8＋770断面后，在同步注浆作用下地面出现隆起；但注浆并不是引起地面隆起的单一因素，切口到达之前，切口附加推力也引起了部分土体上抬。对横断面隆起位移，因Melos等［13－14］仅提供了最终横断面地面位移，无法将切口隆起与注浆隆起加以区分，因此下面的分析粗略地认为地面隆起都由注浆所致。

8＋770断面地面隆起高斯公式及其他方法计算结果见图17及表1。图16可见，隆起曲线关于轴线不对称，故仅分析y＜0一侧。

图17及表1可见，Gaussian公式及Chi法（β＝52°）基本可以反映隆起的趋势，与实测最为接近；Loganathan－Poulos法与实测差别稍大，可近似反映隆起趋势；其他方法，因过大估计了隆起范围，使得计算结果与实测值差别很大。对于该工程，注浆隆起宽度参数与地层损失沉降槽宽度参数比例介于0.86～1.08之间。

2.4 讨论

通过前面3个盾构隧道工程实例分析可见，盾构掘进过程中，盾尾同步注浆可使地面隆起。Gaussian公式和Chi法计算所得隆起位移与实测曲线基本吻合，这主要是因为这2种方法考虑到了土层性质对隆起影响范围的影响；在积累了丰富的注浆隆起实测数据之后，获得注浆隆起参数Vh和地层沉降影响角β的取值范围，基本可以对注浆引起的地面隆起进行预测。Loganathan－Polous计算所得隆起值，在杭州庆春路隧道和马德里地铁沿线工程，也可以大致预测隆起的趋势；其他计算方法，均因过高估计了注浆隆起范围，而使得计算结果与实际有较大出入。

图17 8＋770断面横断面隆起位移实测值及拟合、计算值

由此看来，在本文所述7种方法中预测注浆隆起方法中，Gaussian公式和Chi法精度最高，但需工程经验分别确定Vh和β的取值；在缺乏工程经验的情况下，Loganathan－Poulos法可近似反映隆起的趋势。

3 考虑注浆隆起后的地面位移计算

前面分析可见，对于盾尾注浆引起的横断面地面隆起，基本符合高斯分布。而对隧道施工引起的横断面地面沉降预测，工程实践中应用最为广泛的为Peck公式。注浆隆起后的总的地面位移，既包含地层损失沉降，又包含注浆隆起，因此可以用注浆隆起高斯拟合公式与传统Peck公式叠加来计算。

计算见式（11）～（13）。

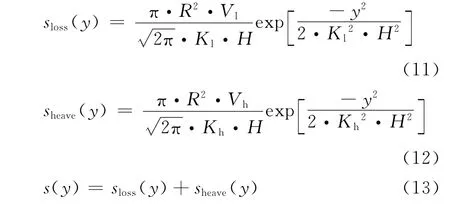
式中：sloss（y）、sheave（y）、s（y）为分别为距隧道轴线y位置处地层损失引起地面位移，注浆隆起引起的地面位移及总位移；Vl，Kl为分别为地层损失沉降的地层损失率与沉降槽宽度参数；Vh、Kh为分别定义为地层补偿率，注浆隆起宽度参数，假定单位长度填充完建筑空隙之后的富余注浆体积为Vg，浆液单位体积失水率为ξ，单位体积硬化收缩率为η，则Vh可初步粗略取为Vh＝Vg·（1－ξ）·（1－η）／（π·R2）。

以杭州庆春路隧道D5断面为例，x＝－35m，横断面地面位移（见图7），距轴线10m之外的地面出现隆起，传统的Peck公式根本无法对其加以拟合。使用式（11）～（13），将注浆隆起考虑在内，拟合得Kl＝0.311，Vl＝－0.270%，Kh＝0.504，Vh＝0.344%。拟合结果见图18。图中可见，考虑了注浆隆起的修正Peck公式，可很好地拟合包含注浆隆起在内的横断面地面位移。

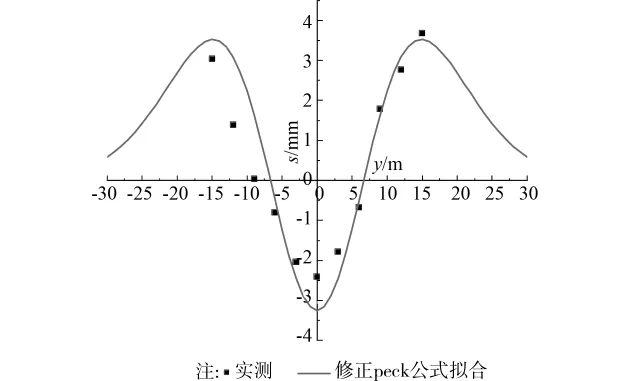
18 D5断面x＝－35m位置横断面地面位移实测值及修正Peck公式拟合值

4 结 论

1）盾构隧道施工过程中，盾尾同步注浆可引起地面土体上抬。

2）盾尾注浆引起的横断面地面隆起曲线，可以用高斯公式和Chi法较好地拟合。通过对实测横断面隆起反分析，可以确定注浆隆起宽度参数Kh和沉降影响角β的取值。在丰富的盾构掘进注浆隆起实测数据基础之上，确定Kh和β取值后，可合理地预测类似土层盾构施工的注浆隆起。

3）经反分析，杭州庆春路隧道Kh取值范围0.504～0.609，是Kl的1.62～2.14倍，β取值介于54°～63°之间；南京长江隧道Kh取值范围0.220～0.352，是Kl的1.07～1.17倍，β取值范围20°～31°；马德里地铁延伸段工程Kh取值在0.486左右，是Kl的0.86～1.08倍，β取值在52°左右。Kh取值一般大于Kl。

4）缺乏Kh和β取值经验时，Loganathan法可近似计算盾尾注浆所致地面隆起。

5）Mindlin法、Sagaseta法、Verruijt－Booker法、Park法均高估了隆起影响范围，与实际注浆隆起出入较大。

6）考虑注浆隆起的修正Peck公式，可以合理地预测包含注浆隆起在内的盾构掘进引起的横断面地面位移。

［1］Mindlin R D.Force at a point in the interior of a semiinfinite solid［J］.Journal of Applied Physics，1936，7（5）：195－202.

［2］Poulos H G，Davis E H.Elastic solutions for soil and rock mechanics［M］.New York：John Wiley ＆ Sons Inc.1974.

［3］Sagaseta C.Analysis of undrained soil deformation due to ground loss［J］.Géotechnique，1987，37（3）：301－320.

［4］Gonzalea C，Sagaseta C.Patterns of soil deformations around tunnels.Application to the extension of Madrid Metro［J］.Computers and Geotechnics，2001，28（6／7）：445－468.

［5］Verruijt A，Booker J R.Surface settlements due to deformation of a tunnel in an elastic halfplane ［J］.Géotechnique，1996，46（4）：753－756.

［6］Loganathan N，Poulos H G.Analytical prediction for tunneling－induced ground movements in clays ［J］.Journal of Geotechnical and Geoenvironmental Engineering，1998，124（9）：846－856.

［7］Chi S Y，Chern J C，Lin C C.Optimized back－analysis for tunneling－induced groundmovement using equivalent ground loss model［J］.Tunnelling and Underground Space Technology，2001，16（3）：159－165.

［8］Park K H.Analytical solution for tunnelling－induced ground movement in clays ［J］.Tunnelling and Underground Space Technology，2005，20（3）：249－261.

［9］Peck R B.Deep excavations and tunneling in soft ground［C］.http：／／State of the Art Report.Proceedings of 7thInternational Conference on Soil Mechanics and Foundation Engineering.Mexico City：［s.n.］，1969：225－290.

［10］Puzrin A M，Burland J B，Standing J R.Simple approach to predicting ground displacements caused by tunnelling in undrained anisotropic elastic soil［J］.Geotechnique，2012，62（4）：341－352.

［11］吴勃英.数值分析原理［M］.北京：科学出版社，2004.

［12］Migliazza M，Chiorboli M，Giani G P.Comparison of analytical method，3Dfinite element model with experimental subsidence measurements resulting from the extension of the Milan underground［J］.Computers and Geotechnics，2009，36（1／2）：113－124.

［13］Melis M，Medina L，Rodríguez J M.Prediction and analysis of subsidence induced by shield tunnelling in the Madrid Metro extension［J］.Canadian Geotechnical Journal，2002，39（6）：1273－1287.

［14］Maynar M M，Rodriguez L M.Predicted versus measured soil movements induced by shield tunnelling in the Madrid Metro extension ［J］.Canadian Geotechnical Journal，2005，42（4）：1160－1172.

［15］肖衡.大直径泥水盾构掘进对土体的扰动研究［D］.北京：北京交通大学，2009：2－34.