动荷载作用下土工格栅应变软化特性

刘飞禹，林青松

（上海大学 土木工程系，上海200072）

土工合成材料自出现以来，已在土木工程实践中得到了广泛应用［1－3］。随着土工加筋技术的研究越来越深入［1－6］，土工合成材料的强度衰减特性也越来越受到重视。胡利文［7］的研究结果表明，土工布经过4a的运行，其强度损失约50%。Leshchinsky等［8］发现聚乙烯土工格栅最大可能应力松弛大约为最初荷载的50%。张功新等［9］通过对实际工程的现场观测，发现筋材的长期强度损失及模量的衰减会降低路堤的长期稳定性，对工后沉降产生不利的影响。Bathurst等［10］研究了循环应力比和加载频率对不同材料格栅循环动力特性的影响。Ling等［11］对PP、PET、HDPE三种土工格栅在循环荷载作用下的拉伸性能做了研究。杨果林等［12］通过加－卸荷循环试验，发现筋材的弹性应变和塑性应变均随应力水平增加而增大。但上述试验循环荷载的作用次数较少，而且都没有考虑预拉力与加载频率对土工格栅动力特性的影响，而在实际工程中对格栅施加预拉力是一种行之有效的方法［13］。理论研究方面，Sawicki［14］在 Leshchinsky的试验基础上，建立了相应的标准流变模型。Perkins［15］在试验的基础上建立了一个非线性、与时间相关的、各向异性的土工加筋材料本构模型。Xiao等［16］建立了土工格栅的双曲线本构模型。Ling等［17］采用一维的边界面模型模拟了循环荷载作用下的动力特性。Liu等［18］采用修正的 Masing准则和边界面模型，建立了循环荷载作用下土工合成材料的动力模型。但以上模型都没有考虑初始预拉力的影响，也没有考虑土工格栅的软化特性与频率的影响。

本文对土工格栅进行了循环拉伸试验，考虑了初始预拉力以及加载频率对格栅应变软化特性的影响，并通过改进Iwan串联模型，建立了土工格栅在循环拉力作用下应力应变关系的表达式。

1 试验内容和方法

采用动静万能试验机进行单向循环拉伸试验，加载波形采用正弦波，由伺服系统自动生成，加载方式为应力控制式。测试材料采用单向土工格栅，见图1，拉伸过程见图2，格珊性能参数见表1。

图1 土工格栅试验试样

图2 土工格栅拉伸过程

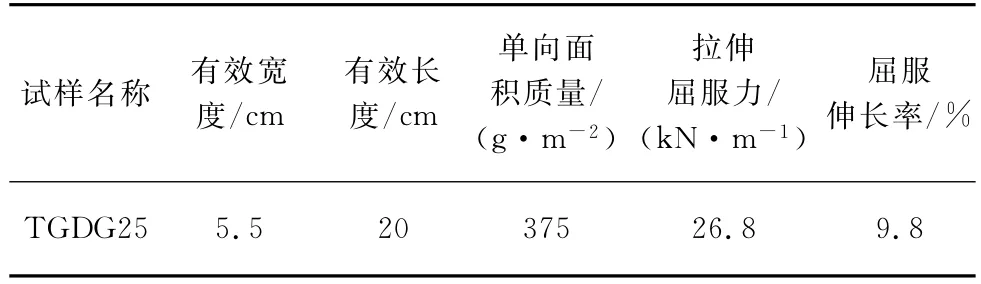
表1 材料性能参数

试验共进行了14组，各组试验的预拉力Tp、荷载频率f、循环拉力Tc的值见文献［19］。

2 试验结果与分析

图3为土工格栅拉伸试验得到的第1次与第N次加载时的滞回曲线。图中E1、EN分别定义为土工格栅第1次与第N次加载时的刚度。参照Idriss等［20］对土体软化指数的定义，定义格栅软化指数δ为式（1）。

图3 土工格栅拉力 应变曲线

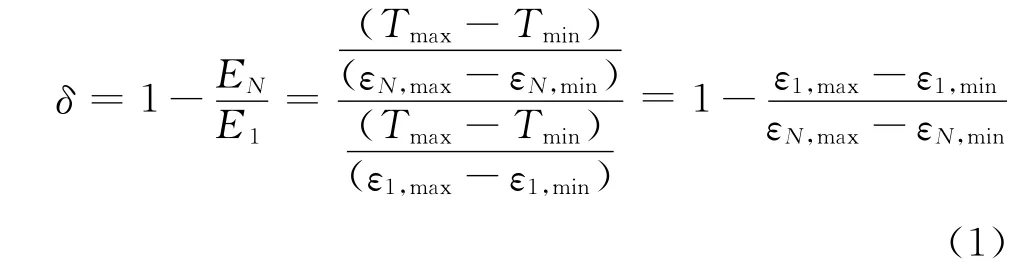
式中：Tmax、Tmin分别为每次加载时的最大与最小拉力；ε1，max、ε1，min分别为第1次加载时最大与最小应变；εN，max、εN，min分别为第N次加载时最大与最小应变。

2.1 循环拉力的影响

图4为循环拉力Tc不同时，软化指数δ与格栅应变ε的关系曲线。图4（a）是不施加预拉力Tp时的曲线，图4（b）是Tp为5kN／m时的曲线，Nmax为每次试验所经受的荷载作用总次数。随着ε的增加，δ逐渐增大。随着Tc的增加，δ增大，且增大速率逐渐加快，在Tc＝5kN／m和10kN／m时，δ差距不是很明显，当Tc增加到15kN／m时，δ增加骤然加快，表明Tc越大对格栅δ影响越显著；随着Tc增加，ε也相应增大，δ与ε的关系曲线逐渐变缓并且显著右移，相同ε时，格栅刚度衰减的更快，从而加速了土工格栅的破坏。

2.2 预拉力的影响

图4 不同Tc时土工格栅的ε－δ曲线

图5 不同Tp时土工格栅的ε－δ曲线

图5为Tp不同时，格栅软化指数δ与应变ε的关系曲线。δ随着ε的增加而增大。δ与ε的关系曲线在Tp为0与5kN／m时，比较接近，Tp增加到10kN／m时，曲线外扩趋势明显。随着Tp增加，δ增大，并且δ的增大趋势随Tp的增加而越来越明显。同时，随着Tp的增加，ε增大，且增大速率也加快，当Tc为5kN／m时，Tp为10kN／m的试件经过10 000次循环荷载作用后的ε与Tp为5kN／m的试件经过53 000次循环荷载作用后的ε相差不大；当Tc为10kN／m 时，Tp为10kN／m的试件经过7 800次循环加载后的ε已远超Tp为5kN／m的试件经过51 000次循环加载后的ε，表明Tp对ε的影响较大。

2.3 荷载频率的影响

图6（a）、6（b）为Tc分别为5kN／m、10kN／m时，不同荷载频率f下格栅的δ与ε关系曲线。δ随着ε的增加而增大。随着f的逐渐减小，δ与ε的关系曲线显著右移，表明ε相同时，格栅刚度有了更大衰减。随着f的逐渐降低，ε发展加快，在图7（a）中，f为0.1Hz经7 000次加载后，其ε与f为1.0Hz经53 000次加载后的ε接近，但远超f为3.0Hz经10 000次加载后的ε，表明f对ε也有较大影响。

图6 f不同时土工格栅的ε－δ曲线

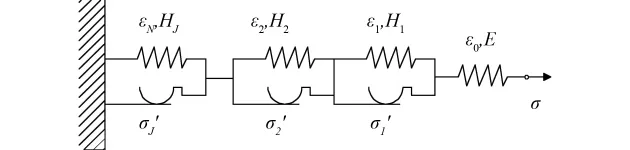
图7 Iwan串联模型

3 土工格栅应变软化模型的建立

关于土工格栅的理论模型研究，目前还较少，而考虑土工格栅软化特性的模型则还未见报道。由于对循环荷载作用下土工格栅应变软化机理的研究还较缺乏，要从理论上建立一个完善的模型还较困难，因此考虑采用根据试验结果进行模拟分析的方法。

从试验结果可以发现，土工格栅的动应力 应变关系曲线与土的动应力 应变关系曲线很相似，因此拟采用改进的土动力学模型来模拟土工格栅的特性。在现有土动力模型中，Iwan串联模型［21］相对较简单，易于应用，因此在此模型基础上进行改进。

Iwan串联模型由一系列线性弹塑性元件串联组成。每一元件由一根刚度为Ei的弹簧和一个屈服应力为σi′的库仑摩阻片组成。摩阻片的个数为J，如图8所示。文献［22］根据多重屈服面运动硬化理论，得到了Iwan模型应力应变的表达式：

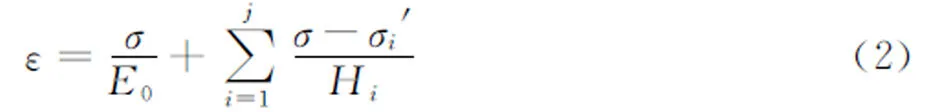
式中：σ为各元件所受应力；j为达到屈服状态的元件的个数；Hi为第i个元件的塑性模量，Hi＝

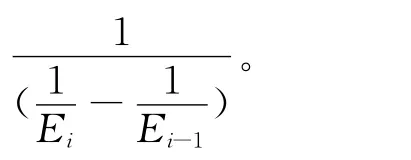
然而，Iwan模型不能反映循环荷载作用下的累积塑性应变。为此，本文在Iwan模型中串联一理想刚塑性元件来考虑格栅的累积塑性应变，如图8所示。

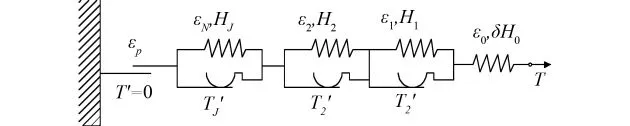
图8 改进的Iwan串联模型

图8中，T为各元件所受拉力，Ti′为各元件的屈服拉应力。假定新加入的单元屈服应力为0，屈服后的应变即为累积塑性应变εp，则总应变为

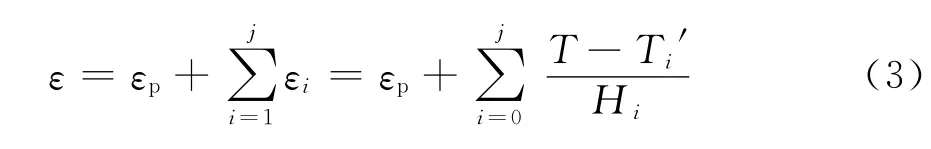
εp是一个与预拉力、频率、软化指数等有关的量，通过对试验数据的分析，发现εp与δ之间存在着二次曲线关系，可用下式表达：

式中A为反映循环拉力、预拉力、频率等因素影响的参数。通过对试验数据的进一步分析，可得到如下表达式：

式中：Tp、f、Tc、δ分别是预拉力、荷载频率、循环拉力和软化指数。Ei可以从土工格栅的加载曲线上得到，屈服拉应力T′i的大小一般认为是在0到循环拉应力幅值间均匀分布，所以各段拉应力增量为。J值的大小对计算精度有较大影响，一般其值在50～100之间可满足计算要求，根据试算的结果，综合考虑计算时间和精度要求，J取80。

将式（4）、（5）代入式（3）就可以得到考虑了软化特性的土工格栅拉力 应变关系表达式。为了验证改进模型的合理性，采用改进的模型编制了计算程序，并与试验结果进行了对比，从图9中可以看出，计算结果与试验结果符合较好，证明了所建模型的正确性。

图9 计算模型的验证

5 结 论

1）随着循环拉力、预拉力的增加，动累积塑性应变逐步增大，软化指数也增大，格栅强度衰减加快。

2）随着荷载频率的逐渐降低，动累积塑性应变发展增快，软化指数也增大，格栅强度衰减加快。

3）通过将改进的Iwan模型计算结果与试验结果进行对比，表明所建模型可以较好的反映土工格栅在循环荷载作用下的动力特性。

［1］Cheble H，Clouteau D，Schmitt L.Dynamic response of high－speed ballasted railway tracks：3Dperiodic model and in situ measurements ［J］.Soil Dynamics and Earthquake Engineering，2008，28（2）：118－131.

［2］Huang J，Han J.3Dcoupled mechanical and hydraulic modeling of a geosynthetic－reinforced deep mixed column－supported embankment ［J］.Geotextiles and Geomembranes，2009，27（4）：272－280.

［3］Briancon L，Simon B.Performance of pile－supported embankment over soft soil：full－scale experiment［J］.Journal of Geotechnical and Geoenvironmental Engineering，2011，137（4）：324－331.

［4］Sadrekarimi A，Olson S M.Shear band formation observed in ring shear tests on sandy soils［J］.Journal of Geotechnical and Geoenvironmental Engineering，2010，136（2）：366－375.

［5］Jones C J F P，Clarke D.The residual strength of geosynthetic reinforcement subjected to accelerated creep testing and simulated seismic events ［J］.Geotextiles and Geomembranes，2007，25（3）：155－169.

［6］Rajesh S，Viswanadham B V S.Centrifuge modeling and instrumentation of geogrid reinforced soil barriers of landfill covers ［J］.Journal of Geotechnical and Geoenvironmental Engineering，2011，137（4）：332－342.

［7］胡利文.深圳河反滤土工布试验研究［J］.岩土工程学报，2002，24（3）：351－355.HU Liwen.Experimental study on filter geotextiles applied in Shenzhen River project［J］.Chinese Journal of Geotechnical Engineering，2002，24（3）：351－355.

［8］Leshchinsky D，Dechasakulsom M，Kaliakin V，et al.Creep and stress relaxation of geogrids［J］.Geosynthetics International，1997，4（5）：463－479.

［9］张功新，莫海鸿，曾庆军，等.土工合成材料对路堤长期稳定性及工后沉降的负面影响分析［J］.岩土工程学报，2005，27（5）：686－689.ZHANG Gongxin，MO Haihong，ZENG Qingjun，et al.Analysis of negative effect of geotextile on long－term stability and post－construction settlement of embankment［J］.Chinese Journal of Geotechnical Engineering，2005，27（5）：686－689.

［10］Bathurst R，Cai Z.In－isolation cyclic load－extension behavior of two geogrids ［J］.Geosynthetics International，1994，1（1）：1－19.

［11］Ling H，Mohri Y，Kawabata T.Tensile properties of geogrids under cyclic loadings ［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，1998，124（8）：782－787.

［12］杨果林，王永和.土工合成材料在加卸循环荷载作用下的应力应变特性研究［J］.铁道学报，2002，24（3）：74－77.YANG Guolin，WANG Yonghe.Study on stress－strain relationship of geosynthetics under cyclic loading［J］.Journal of the China Railway Society，2002，24（3）：74－77.

［13］徐少曼，林瑞良，康进王.提高路堤下软基土工织物加筋效果的综合措施［J］.中国公路学报，2003，16（2）：42－44.XU Shaoman，LIN Ruiliang，KANG Jinwang.Multiplemeasures to improve reinforced effect of soft cohesive subsoil under embankment by geotextile ［J］.China Journal of Highway and Transport，2003，16（2）：42－44.

［14］Sawicki A.A basis for modelling creep and stress relaxation behavior of geogrids ［J］.Geosynthetics International，1998，5（6）：637－645.

［15］Perkins S W.Constitutive modeling of geosynthetics［J］.Geotextiles and Geomembranes，2000，18（5）：273－292.

［16］Xiao C Z，Luan M T，Yang Q，et al.An experimental study on creep behaviour and hyperbolic constitutive model of geogrids with applications ［J］.Ground Modification and Seismic Mitigation，2006，152（3）：281－286.

［17］Ling H I，Liu Z.Performance of geosynthetic－reinforced asphalt pavements ［J］.Journal of Geotechnical and Geoenvironmental Engineering，2001，127（2）：177－184.

［18］Liu H，Ling H I.Modeling cyclic behavior of geosynthetics using mathematical functions combined with Masing rule and bounding surface plasticity［J］.Geosynthetics International，2006，13（6）：234－245.

［19］张孟喜，林青松，刘飞禹.循环荷载作用下土工格栅拉伸试验研究［J］.岩土力学，2010，31（7）：2024－2029.ZHANG Mengxi，LIN Qingsong，LIU Feiyu.Tensile experiments of geogrids under cyclic loading［J］.Rock and Soil Mechanics，2010，31（7）：2024－2029.

［20］Idriss I M，Dobry R，Singh R D.Nonlinear behavior of soft clays during cyclic loading ［J］.Journal of Soil Mechanics and Foundation，1978，104（12）：1427－1447.

［21］Iwan W D.On a class of models for the yielding behavior of continuous and composite systems ［J］.Journal of Applied Mechanics，1967，43：612－617.

［22］Puzrin A M，Houlsby G T.Fundamentals of kinematic hardening hyperplasticity［J］.International Journal of Solids and Structures，2001，38（21）：3771－3794.