远震相对走时数据快速计算方法及应用

江国明，张贵宾，徐 峣

中国地质大学（北京）地球物理与信息技术学院，北京 100083

1 引 言

天然地震层析成像技术已被广泛地应用于研究地球内部速度结构，并取得了丰硕的地质成果［1－5］.尤其是远震层析成像技术，由于其远震射线可穿越较深的地层，因此对于探索地球深部圈层结构、板块深俯冲特征等地学问题均具有得天独厚的优势.目前，远震体波层析成像技术采用的数据通常是初至震相的相对走时残差值［4］，其优点是可以最大程度地消除震源位置、发震时刻以及研究区域以外射线路径等因素引起的走时误差.实际上，从远震波形资料中无法直接获得相对走时残差信息，最常用的方法是：首先获得初至震相的观测到时和理论到时，然后两者相减得到走时残差，最后将观测到时减掉走时残差的平均值，即可得到相对走时残差（具体计算过程可参阅本文第2部分）.不难看出，通过这种方式得到的相对走时残差数据的精度在很大程度上取决于初至到时的精度，而这一精度又直接决定着成像结果的可信度.从波形资料中获得初至到时的方法主要包括人工手动识别法和计算机自动检测法.人工手动识别法尽管实施步骤简单，但对于信噪比较低的地震波形资料，则无法满足精度要求，并且工作效率较低、劳动强度大，因此应用范围有限；而计算机自动检测法由于其精度和效率双高的特点已愈来愈受到研究者们的青睐，比如AIC到时检测技术［6－7］、相对和绝对走时差的模拟退火法［8］以及多尺度小波变换法［9］等.尽管这些方法采用不同的原理实现了初至到时自动识别的目的，但大多数方法仅采用了波形的振幅信息，而忽略了相位信息.由于许多自动识别技术中涉及到了多道互相关方法，而且该方法与本文的研究内容存在直接关系，因此下面简单介绍一下多道互相关方法.

VanDecar和Crosson［10］提出多道互相关（multichannel cross－correlation）技术实现了初至到时数据的自动获取（简称“MCCC方法”），不但大大地降低了人力资本，而且提高了数据精度.因此，多道互相关技术在地震走时数据处理领域得到了广泛的应用.但是，MCCC方法最大的缺陷是在计算绝对走时数据时必须求解超定方程组，而这在一定程度上势必降低走时数据的计算精度［11］.Rawlinson和Kennett［12］提出了自适应叠加方法（adaptive stacking）计算绝对走时和相对走时残差数据（简称“Rawlinson方法”），其原理是利用波形叠加技术直接获得任意两道地震记录之间的走时残差，然后以选定的某一震相到时为参考时间并通过迭代的方式得到最佳的绝对走时和相对走时数据，从而避开了MCCC方法中求解超定方程组的麻烦.然而，在Rawlinson方法中，当对任意两个波形数据进行叠加时，仅仅使用了波形的时间和振幅信息，而忽略了相位信息.对于信噪比低的波形资料，如果在波形叠加时仅利用振幅信息，可能无法很好地压制噪声，但若将相位信息作为权重因子而引入到波形叠加计算中，那么可以达到提高信噪比的目的，这就是相位权重叠加（phaseweighted stack）原理［13］.

目前，针对如何从远震波形资料中自动获取高精度的相对走时残差信息的问题，国内鲜有文献对此提出详细而完整的解决方案.本文将利用相位权重叠加技术对此问题提出一种快速计算方法.整个计算过程全部由计算机程序自动完成，不但节约了人力资源，而且提高了工作效率.为验证新方法的可靠性和实用性，我们选取长江中下游地区的远震波形资料为例进行分析和讨论.

2 计算原理

在近震层析成像中，所用的数据为绝对走时［3］；而在远震层析成像中，所用的数据则是相对走时残差［4］.下面简单介绍一下相对走时残差的常规计算步骤.

假设第i个远震发生后，被M个台站观测到.其中，从第j个台站记录的波形中手动拾取到的初至震相观测到时记为，其理论到时记为，则该震相的走时残差tij为

那么相对走时残差rij为

图1 波形互相关计算原理图Fig.1 Theoretical diagram of calculating cross-correlation beween waveforms

仍以上述的M条数据为例进行说明.假设第j条和第k条波形如图1中子图所示（时间窗宽度为12s），分别记为Sj（t）和Sk（t），则两波形数据之间的互相关（cross－correlation）系数为：

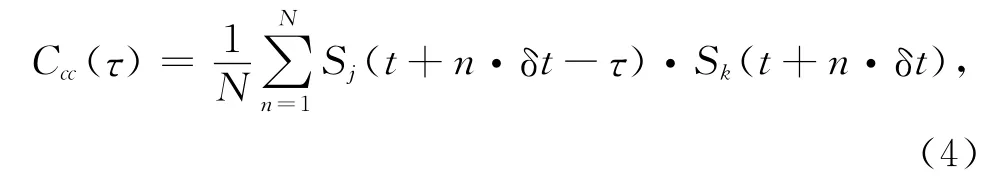
其中，N为时间窗内的采样点数；δt为波形采样间隔；τ为偏移时间；t为时间窗的开始时刻.本例中，前三个参数分别为1201点、0.01s和［－2，＋2］s（变化范围，与图1横轴区间相同）.实际计算时，将计算步长与采样间隔保持一致.图1显示了互相关系数曲线.根据极值点很容易确定第k条波形相对于第j条波形初至震相的到时差为1.28s.同理，利用公式（4）可快速计算得到所有M条波形的初至震相对于第j条波形的到时差数据，共M个（其中，第j条波形相对于自身的到时差为0s），记为

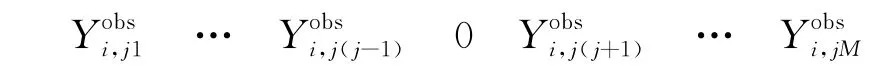
此外，根据每条波形初至震相的理论到时可计算得到M个相对于第j条波形的理论到时差数据，记为这一结果恰好是公式（3）中的相对走时残差.

根据公式（5）～（9），我们提出了计算相对走时残差的一种新思路：首先根据公式（7）和（8）分别计算得到和，然后两者相减得到相对走时残差.如前所述，公式（7）中的参量可根据互相关原理计算得到，而公式（8）中的参量可直接由理论到时（或走时）计算得到，因此计算相对走时残差数据的整个过程完全由计算机程序自动完成.这将大大提高远震数据处理的效率和精度，为将来处理海量数据提供了保障.

然而，利用公式（4）计算任意两条波形的互相关系数时，仅仅利用了波形的振幅信息.当波形资料的信噪比较高时，这样计算是满足要求的；但当波形的信噪比较差时，将很难依据互相关系数确定两波形之间最佳的偏移时间（即走时差）.为此，我们根据相位权重叠加原理［13］和几何归一化互相关（geometric normalized cross－correlation）计 算 思 想［15］在 公 式（4）中引入相位信息，并对互相关系数进行归一化，便得到了改进后的互相关系数计算公式：其中φj、φk分别为第j条和第k条波形的瞬时相位角（弧度）；下标mmcc则表示采用改进后的公式计算的多道互相关系数（modified multi－channel crosscorrelation，简称MMCC）；上标ν代表相位权重因子（一般取2或3）.我们将本文提出的新方法命名为MMCC方法.

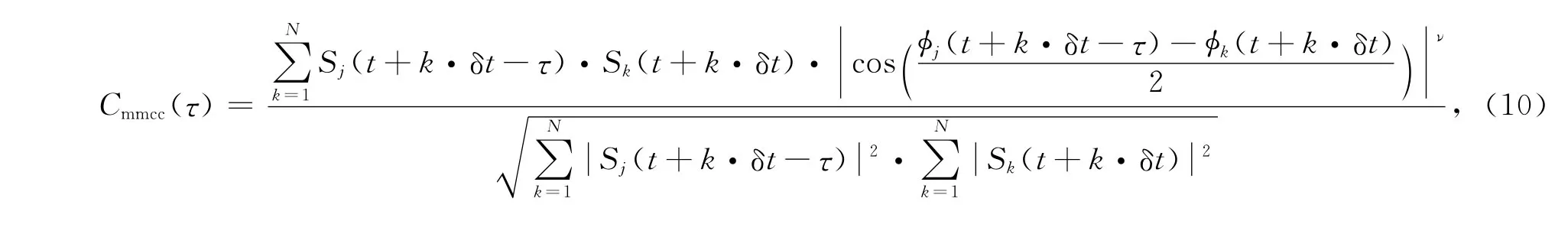
值得说明的是，地震波形的瞬时相位角是无法直接从波形资料中获取的，通常的做法是：先对地震波形数据S（t）进行希尔伯特变换得到H（t），然后利用公式φ＝arctan［H（t）／S（t）］计算得到.

至此，我们根据多道互相关技术和相位权重叠加技术实现了远震数据中相对走时残差的自动计算，现在总结一下具体步骤：

（1）对原始的地震波形资料进行滤波去噪处理；

（2）对预处理后的波形资料进行希尔伯特变换，计算瞬时相位角；

（3）设定时间窗口，利用公式（10）计算任意两条波形之间的互相关系数并确定最佳的偏移时间（即走时差）.若有M条波形数据，则需计算M·（M－1）／2次；

（4）利用TauP软件，计算每条远震波形中初至震相的理论走时（或到时），和任意两条波形之间的理论走时残差（或到时残差）；

（5）根据公式（5）～（9），计算相对走时残差.

3 实例与讨论

为了验证MMCC方法的可行性和高效性，我们以长江中下游地区的远震波形资料为例，采用本文提出的新方法和常规方法分别计算初至震相的相对走时残差.所用的远震波形数据由国家数字测震台网数据备份中心提供，记录时间范围为2009年11月—2011年4月，采样率为每秒100次.图2显示了安徽和江苏两省的47个省台台站位置（黑色方块）.我们以发生在印尼的某一次远震的16条波形数据为例进行后文阐述（台站位置如图2中五角星所示）.

首先，以图3中的16条远震波形的头文件信息为基础，构建图4a所示的理论波形（不含噪声），即震源信息和理论走时与真实波形完全一致（表1），而以分布在［0，2］区间内的伪随机数作为理论波形的走时残差（表1第6列）.采用常规方法和MMCC方法分别计算16条理论波形的相对走时残差，所得结果分别如表1第7列和第8列所示.对比后，不难发现两者几乎相等，这充分说明我们提出的MMCC方法和编写的程序均是正确可行的.

此外，为了说明利用MMCC方法计算得到的偏移时间是正确的，我们采用以下方法进行验证：

（1）选择参考波形.在本例中，共16条波形数据.任意一条波形均可与其它15条波形进行互相关计算，于是得到15个互相关系数，然后求平均，将所得平均值记为该波形的互相关值.比较16条波形的互相关值，将具有最大互相关值的那条波形作为参考波形.依据此原则，本例中第7条波形作为参考波形（图4b）；

（2）波形偏移.利用公式（10）计算所有波形相对于参考波形的偏移时间，然后将每条波形按照偏移时间进行偏移.若偏移时间为正，则波形向右移动；反之亦然.图4b显示了偏移后的波形，不难看出，初至震相的相位已对齐，说明计算得到的偏移时间是正确的.

然后，我们对16条理论波形数据加入随机噪声（均值为0而方差为1的正态分布随机数）构建信噪比较低的理论波形（图5a），从波形中已无法识别初至波的到时.采用MMCC方法对含噪声的理论波形计算相对走时残差，结果如表1第9列所示.为了说明MMCC方法中相位信息的重要性，在计算过程中将公式（10）中的ν＝0，即不考虑相位信息，所得结果见表1第10列；然后分别计算表1中第9列和第10列与第7列之差的均方根值，其结果分别为0.058s和0.105s.对比两个均方根值，不难看出第9列的数据精度比第10列高.造成这一差异的最根本原因是：计算第9列结果时考虑了相位信息，而第10列结果未考虑，这充分说明了相位信息对计算相对走时残差的精度具有重要影响.结合前文思路，我们对含噪声的波形根据由MMCC方法计算得到的偏移时间进行偏移，如图5b所示，可以看到尽管波形的信噪比很低，但偏移后的波形初至震相几乎也能对齐，这从侧面说明了MMCC方法具有较强的抗噪能力.

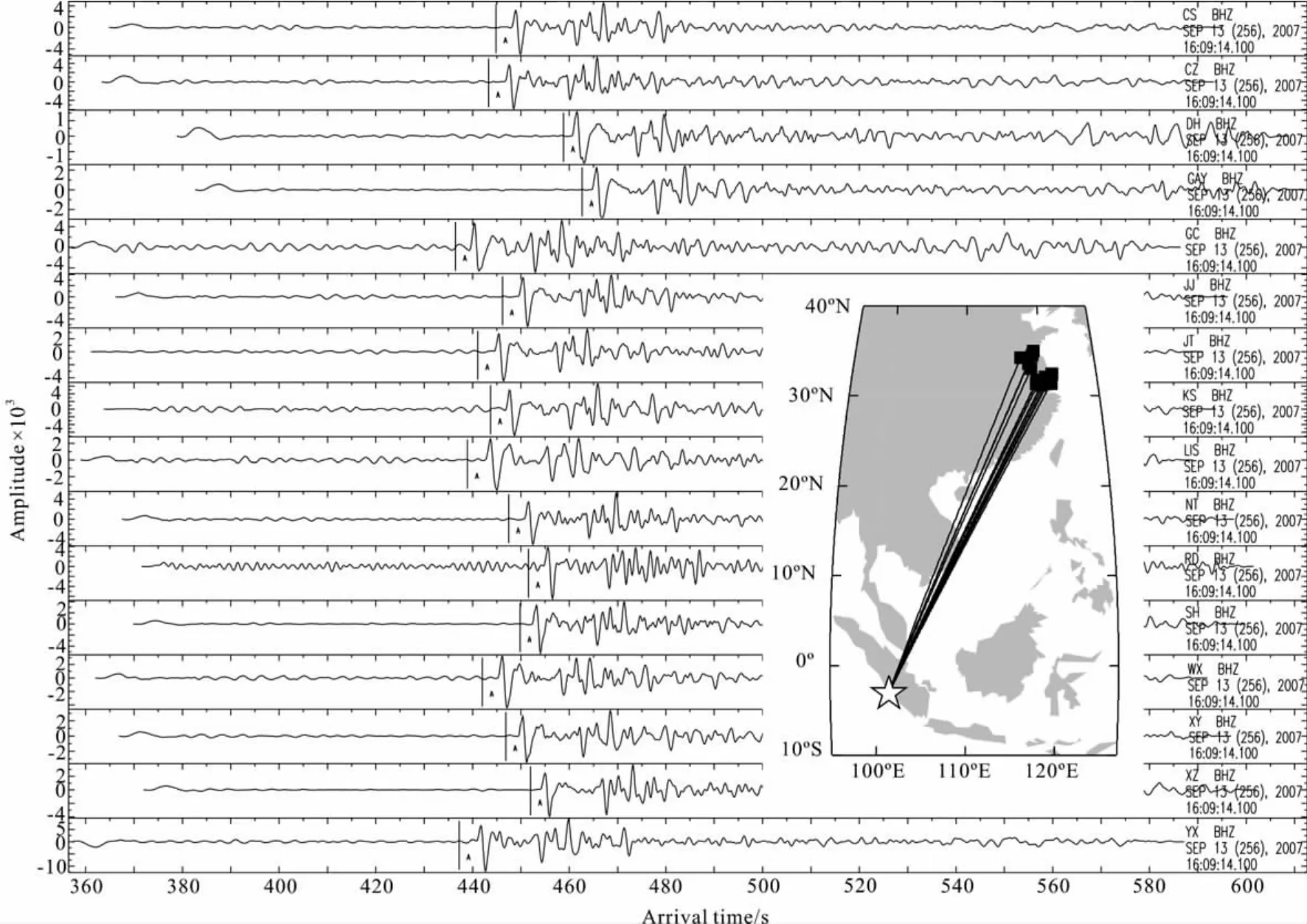
图3 远震波形示例（印尼地区某地震）.横轴零点为发震时刻.短竖线表示理论到时.插图显示了震中、台站和射线分布情况Fig.3 An example of teleseismic data （one event occurred in Indonesia）.The zero point in the horizontal axis is the original time of earthquake.The short vertical line represents the calculated arrival time.This hypocenter，the recorded stations and the corresponding rays are shown in the inserted figure

图4 地震波形经时间偏移前后对比（横轴时刻均相对于理论到时）.（a）偏移前；（b）偏移后Fig.4 Comparison of seismograms without and with correction of offset time（The time values in the horizontal axis are relative to the calculate arrival times）.（a）Before shift；（b）After shift

图5 地震波形（含噪声）经时间偏移前后对比（a）偏移前；（b）偏移后.Fig.5 Comparison of seismograms（including noises）without and with correction of offset time（a）Before shift；（b）After shift.

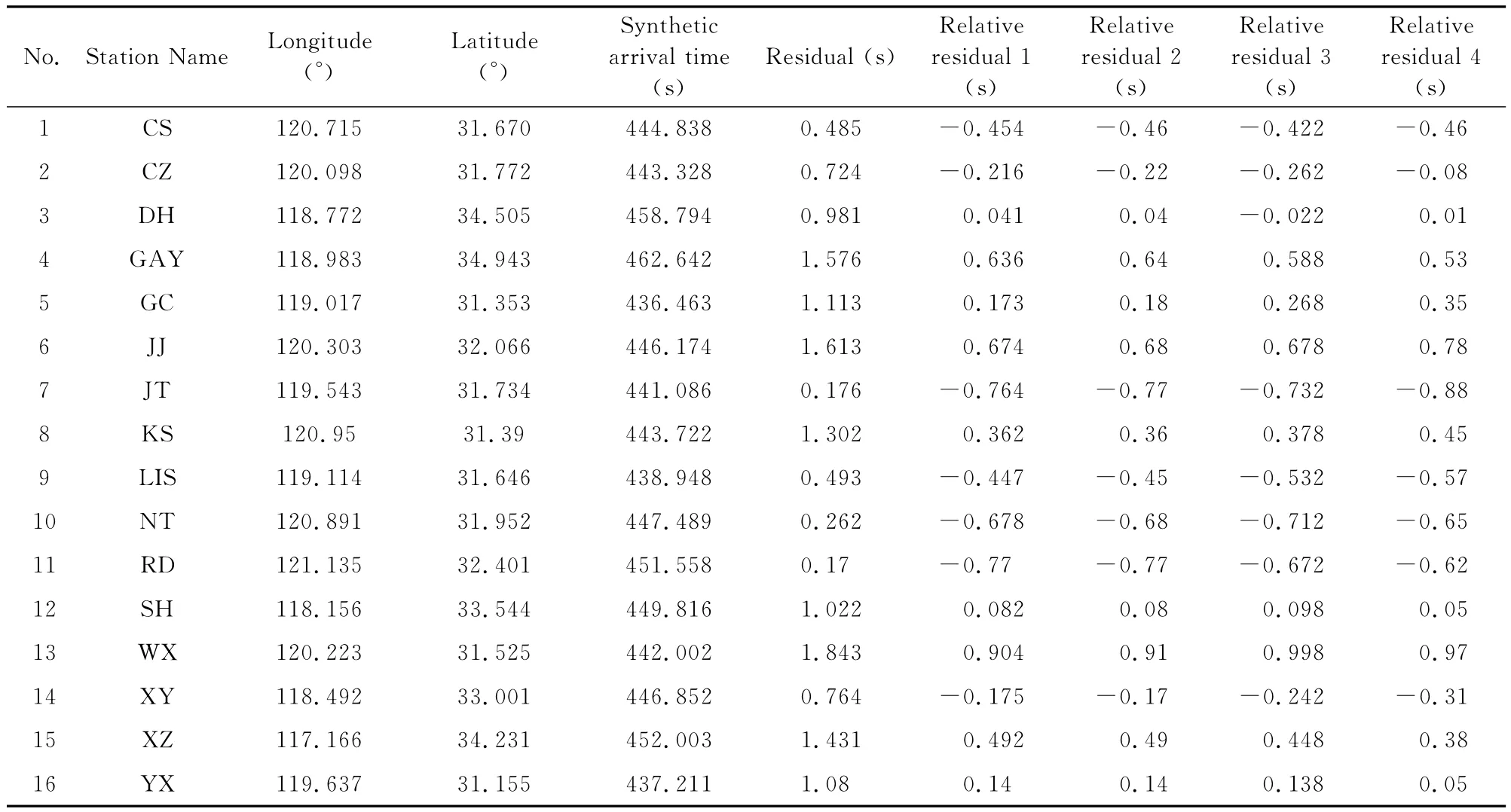
表1 理论波形数据的计算结果对比Table 1 Comparison of the calculation result of synthetic waveform data

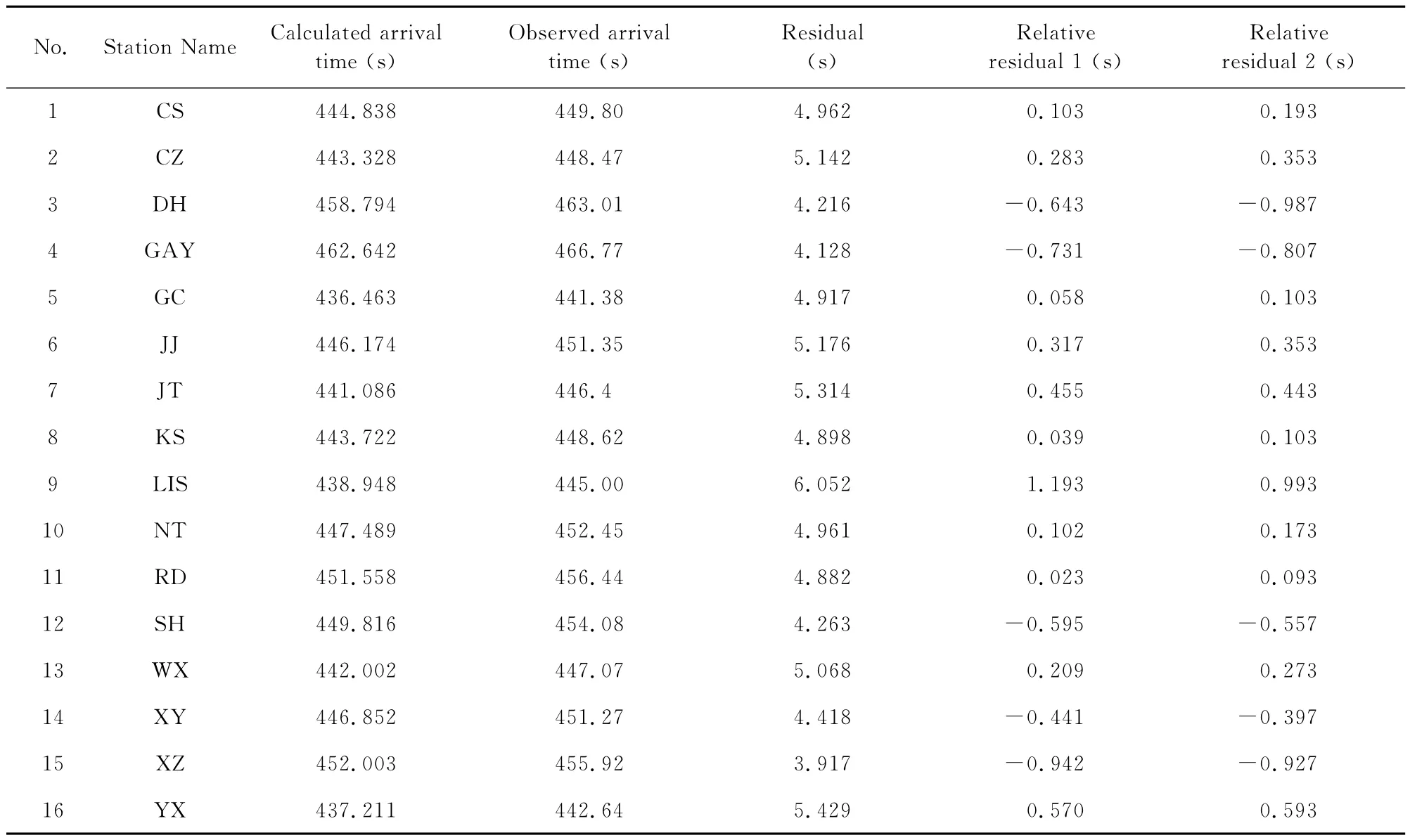
表2 实际波形数据的计算结果对比Table 2 Comparison of the calculation result of real waveform data

最后，我们采用常规方法和MMCC方法分别计算图3中实际波形初至震相的相对走时残差.当采用常规方法进行计算时，必须先获得观测到时.这里采用人工手动拾取的方式得到初至震相的观测到时（表2第4列）；然后减掉理论到时（表2第3列），得到走时残差（表2第5列）；最后利用公式（1）～（3）计算得到常规方法下的相对走时残差（表2第6列）.而利用MMCC方法计算时，所有过程均由计算机程序自动完成，最后得到MMCC方法下的相对走时残差（表2第7列）.对比两种方法得到的结果（即表2第6列和第7列），可以看出两者的变化趋势完全一致.但从这个简单的例子中，还无法判定哪种结果更好.为了使分析结果具有统计意义，我们采用以上两种方法分别处理47个省台记录到的全部13000余条远震波形数据.在获得相对走时残差的基础上，计算每个台站所记录数据的相对走时残差的均方根（Root Mean Square，简称 RMS），并将结果显示于图6中.从图6中，我们清晰地看到采用MMCC方法得到的相对走时残差的RMS值几乎均小于由常规方法获得的结果，这充分证实了MMCC方法的可靠性和优越性，为将来的进一步推广提供了保障.

在获得相对走时残差数据后，可利用远震层析成像技术进一步反演研究区域下方的深部速度结构.在此，我们根据相对走时残差的数值大小粗略分析台站下方地层的构造特征.将每个台站记录到的相对走时残差数据求平均，并将结果示于图7中，不难看出位于郯庐断层西侧的大部分台站上的平均相对走时残差为负值，说明这些台站下方地层内存在高速异常体；而位于断层东侧的大部分台站上的平均相对走时残差为正值，说明台站下方地层内存在低速异常体.这些地层结构特征与其他学者的研究结果基本一致［16－17］.

下面对MMCC方法进行以下几点分析与讨论：

（1）MMCC方法的全部处理过程均由计算机自动完成，无需人为干预，不仅节约了人力资源，而且提高了工作效率和数据精度.为了充分发挥MMCC方法全程自动化的优点，我们编制了相应的脚本和模块，主要包括波形预处理模块、互相关系数计算模块和相对走时残差计算模块；

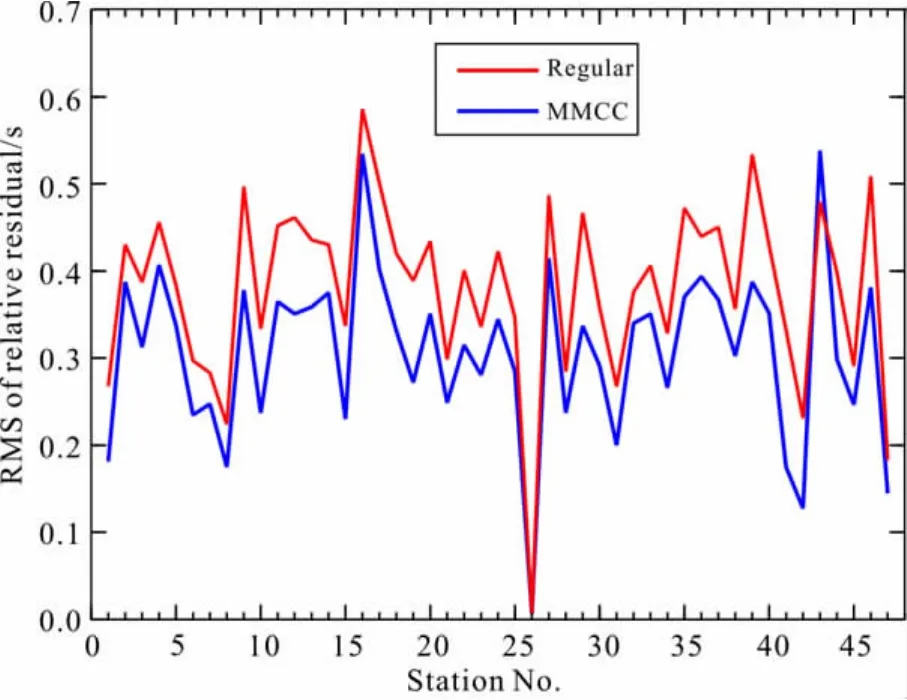
图6 常规与新方法的相对走时残差均方根结果对比.红色和蓝色折线分别表示常规方法（Regular）和新方法（MMCC）的计算结果Fig.6 Comparison of RMS of relative residuals respectively obtained by regular and new improved methods.The red and blue lines respectively represent the results of regular and new improved methods（MMCC）

图7 长江中下游地区省台平均相对走时残差分布Fig.7 Distribution of average relative residuals at provincial stations in the region of middle－lower Yangtze River

（2）利用MMCC方法在计算互相关系数时，由于充分考虑了波形相位信息，因此能够处理信噪比较低的波形数据，这是比MCCC方法和Rawlinson方法优越的地方.我国的固定台站（国家台网和各省省台）一般布设在人类活动较少的地区，所以记录的信号信噪比一般较高，但流动台站由于受到种种因素限制而无法像固定台站那样布设，特别是我国东部地区，由于人为活动较为频繁，流动台站记录到的信号信噪比一般较差.目前，我们已经搜集到了长江中下游地区的流动台站波形数据，并采用MMCC方法进行处理得到了较为理想的结果.

（3）在 VanDecar和 Crosson［10］提出的 MCCC方法中，一般是先根据互相关方法获得走时残差，然后再求解超定方程组得到绝对到时，最后计算得到相对走时残差.我们提出的MMCC方法在计算过程中摒弃了求解超定方程组的步骤，而是由波形数据直接计算得到相对走时残差，这在一定程度上提高了其计算精度.

（4）尽管 MMCC方法可以得到精度较高的远震相对走时残差数据，但前提条件是必须确定理论到时.本文是利用TauP软件［14］在一维速度模型的基础上自动计算理论到时的.目前，全球一维模型有很 多，比 如 Jeffreys－Bullen（J－B）［18］、PREM［19］、iasp91［20］、SP6［21］和 AK135［22］等.本 研 究 中 选 用iasp91模型作为一维速度模型.此外，台站高程对计算理论到时具有直接影响，进而影响相对走时残差的计算.但我们采用的TauP软件计算理论到时时并未考虑台站高程的影响，因此在今后的研究中还需对此进行高程校正，提高计算精度.

4 结 论

远震层析成像技术在研究地球深部速度结构方面发挥着越来越重要的作用，而所用的相对走时残差数据的精度直接决定着成像结果的可信度，因此如何从海量的远震波形资料，特别是信噪比稍差的波形资料中自动获取高精度的相对走时残差数据已成为地震学家亟需解决的问题.国外一些研究者已提出了相应的解决方案，基本思路是：首先根据波形间的互相关性计算走时残差；然后由走时残差经过反演或根据参考到时得到绝对到时；最后整理得到相对走时残差.这一思路最大的优点是无需人工手动拾取震相到时.而国内鲜有学者关于该问题进行系统和详细的阐述.

本文为了处理信噪比较差的远震波形数据，在国内外学者研究成果的基础上，提出了一种新的计算远震相对走时数据的方法.相对于国外学者的方法，我们主要进行了两方面的改进：（1）在计算两波形的互相关系数时引入波形相位信息，有效压制噪声，提高有效震相的识别能力；（2）在确定震相理论到时的前提下，由互相关技术得到的走时残差直接转换成相对走时残差，无需任何的反演或参考时间信息.这些改进使得新方法（MMCC方法）在处理远震波形数据时具有更加强大的适用能力.为了验证新方法的可行性和实用性，我们进行了理论推导和实例验证.理论推导可以保证新方法的计算过程是可行和可信的；实例验证则定量地表明新方法的全自动化和高精度的优点，并将分析结果与其他学者的研究成果进行对比，说明新方法的可信性.然而，尽管新方法在计算远震相对走时残差数据的精度达到0.01s（与采样间隔一致），但无法确定初至震相的绝对到时.

（References）

［1］郭飚，刘启元，陈九辉等.中国境内天山地壳上地幔结构的地震层析成像.地球物理学报，2006，49（6）：1693－1700.Guo B，Liu Q Y，Chen J H，et al.Seismic tomography of the crust and upper mantle structure underneath the Chinese Tianshan.Chinese J.Geophys.（in Chinese），2006，49（6）：1693－1700.

［2］田有，赵大鹏，孙若昧等.1992年美国加州兰德斯地震——地壳结构不均匀性对地震发生的影响.地球物理学报，2007，50（5）：1488－1496.Tian Y，Zhao D P，Sun R M，et al.The 1992Landers earthquake：Effect of crustal heterogeneity on earthquake generation.Chinese J.Geophys.（in Chinese），2007，50（5）：1488－1496.

［3］Zhao D P，Hasegawa A，Horiuchi S.Tomographic imaging of P and S wave velocity structure beneath northeastern Japan.J.Geophys.Res.，1992，97（B13）：19909－19928.

［4］Zhao D P，Hasegawa A，Kanamori H.Deep structure of Japan subduction zone as derived from local，regional，and teleseismic events.J.Geophys.Res.，1994，99（B11）：22313－22329.

［5］Huang J L，Zhao D P.High－resolution mantle tomography of China and surrounding regions.J.Geophys.Res.，2006，111：B09305，doi：10.1029／2005JB004066.

［6］Sleeman R，Orild V E.Robust automatic P－phase picking：An on－line implementation in the analysis of broadband seismogram recordings.Phys.Earth Planet.Inter.，1999，113（1－4）：265－275.

［7］王继，陈九辉，刘启元等.流动地震台阵观测初至震相的自动检测.地震学报，2006，28（1）：42－51.Wang J，Chen J H，Liu Q Y，et al.Automatic onset phase picking for portable seismic array observation. Acta Seismologica Sinica （in Chinese），2006，28（1）：42－51.

［8］Bear L K，Pavlis G L.Multi－channel estimation of time residuals from broadband seismic data using multi－wavelets.Bull.Seismological Soc.Am.，1999，89（3）：681－692.

［9］Chevrot S.Optimal measurement of relative and absolute delay times by simulated annealing.Geophys.J.Int.，2002，151（1）：164－171.

［10］Van Decar J C，Crosson R S.Determination of teleseismic relative phase arrival times using multi－channel crosscorrelation and least squares.Bull.Seismological Soc.Am.，1990，80（1）：150－169.

［11］王家映.地球物理反演理论（第二版）.北京：高等教育出版社，2002.Wang J Y.Inverse Theory in Geophysics.2nd ed.（in Chinese）.Beijing：Higher Education Press，2002.

［12］Rawlinson N，Kennett B L N.Rapid estimation of relative and absolute delay times across a network by adaptive stacking.Geophys.J.Int.，2004，157（1）：332－340.

［13］Schimmel M，Paulssen H.Noise reduction and detection of weak，coherent signals through phase－weighted stacks.Geophys.J.Int.，1997，130（2）：497－505.

［14］Crotwell H P，Owens T J，Ritsema J.The TauP toolkit：flexible seismic travel－time and ray－path utilities.Seism.Res.Lett.，1999，70（2）：154－160.

［15］Schimmel M.Phase cross－correlations：Design，comparisons，and applications.Bull.Seism.Soc.Am.，1999，89（5）：1366－1378.

［16］Chen L，Zheng T Y，Xu W W.A thinned lithospheric image of the Tanlu Fault Zone，eastern China：Constructed from wave equation based receiver function migration.J.Geophys.Res.，2006，111：B09312，doi：10.1029／2005JB003974.

［17］吴福元，孙德有.中国东部中生代岩浆作用与岩石圈减薄.长春科技大学学报，1999，29（4）：313－318.Wu F Y，Sun D Y. The Mesozoic magmatism and lithospheric thinning in Eastern China.J.Changchun Univ.Sci.Technol.（in Chinese），1999，29（4）：313－318.

［18］Jeffreys S H，Bullen K E.Seismological Tables.London：Gray Milne Trust，1940.

［19］Dziewonski A M，Anderson D L.Preliminary reference Earth model.Phys.Earth Planet Inter.，1981，25（4）：297－356.

［20］Kennett B L N，Engdahl E R.Travel times for global earthquake location and phase identification.Geophys.J.Int.，1991，105（2）：429－466.

［21］Morelli A，Dziewonski A M.Body－wave traveltimes and a spherically symmetric P－and S－wave velocity model.Geophys.J.Int.，1993，112（2）：178－194.

［22］Kennett B L N，Engdahl E R，Buland R.Constraints on seismic velocities in the Earth from traveltimes.Geophys.J.Int.，1995，122（1）：108－124.

［23］Wessel P，Smith W H F.New，improved version of generic mapping tools released.Eos Trans.AGU，1998，79（47）：579，doi：10.1029／98EO00426.