人工电磁材料的多尺度分析
2012-08-09逯贵祯殷红成李彦霏
逯贵祯 殷红成 李彦霏 韦 笑,
(1.中国传媒大学信息工程学院,北京100024;2.电磁散射重点实验室,北京100854)
引 言
人工电磁材料可以通过人工方法形成所需要的电磁特性。近几十年来,随着人工电磁材料研究的不断深入,新的应用不断出现[1]。在人工电磁材料的理论研究中,关键问题之一是如何通过人工结构合成所需要的电磁材料。因此,研究微周期结构和宏观等效电磁参数是一项非常重要的研究内容。
二十世纪七、八十年代由Lions提出并发展的多尺度分析方法[2]是描述复合材料结构非均匀场的有效工具。该方法的实质是用均质的宏观结构和非均质的微观结构描述周期性复合材料结构;将物理量表示成关于宏观坐标和微观坐标的渐近展开函数,并用微观和宏观两种尺度之比做小参数展开,用微扰方法将原问题转化为微尺度问题和大尺度问题。微尺度问题和大尺度问题的均匀化偏微分方程均通过有限元方法进行求解。
有限元多尺度方法[3]是目前研究的热点。针对不同的学科,多尺度方法都有广泛的应用。在多尺度方法中,根据所研究问题的几何特征,将几何结构分为宏观结构和微尺度结构。对宏观结构进行均匀化,用微尺度结构分析的结果对宏观结构进行修正。目前大多数多尺度问题的研究是针对多孔材料,研究热导率、热力耦合问题等标量场的偏微分方程。针对矢量电磁场问题的研究,文献[5]给出了矢量麦克斯韦方程的多尺度问题的数学证明。在该文献中,微尺度修正项采用了旋度场。文献[6-7]针对三维电磁场提出了采用无旋场作为修正项的多尺度方程,对方程进行了有限元求解,得到了多尺度分析结果。该结果与Maxwell Garnett近似的结果[9]进行了比较,两种结果吻合较好。
但是,目前关于电磁场多尺度的分析尚不能说明人工电磁材料的很多新特性。尽管文献[2]的结果与Maxwell Garnett近似[9]的结果符合较好,然而这只是针对准静态情况。如果有旋场产生很大修正项,将无法使用目前的理论。针对这一问题,本文提出了一种考虑有旋和有散场作为修正项的新的多尺度分析方法,适用于任意矢量场的情况,可用于分析与微尺度和频率有关的多尺度修正问题。
从麦克斯韦方程出发,给出了多尺度问题的微尺度泛函方程,利用该方程得到了微尺度结构的修正场分布和等效电磁参数。与采用细分网格的有限元分析相比,两种计算结果一致性较好,证明了所提方程的有效性。
1 新的多尺度有限元公式
在复合材料的多尺度问题中,均匀背景材料中加有不同参数的物质,该物质呈现周期分布结构。在用传统方法求解该问题过程中,由于所加结构物质的尺度比较小,所以数值计算需要使用非常小的网格,造成计算量的大量增加。在多尺度方法中,将不同尺度问题分别处理。对小尺度结构建立微尺度泛函方程,对大尺度问题,建立均匀化的泛函方程,分别求解大小尺度方程,最后得到多尺度问题的解。下面考虑三维麦克斯韦方程组在复合材料结构中的多尺度问题求解。三维空间麦克斯韦方程组为

由方程(1)可得无源区关于电场矢量的微分方程
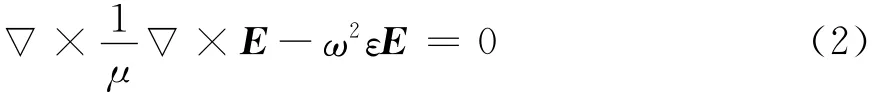
在多尺度问题中,用ξ表示微尺度变量,大尺度变量用x表示,多尺度问题的电场可以表示为平均场与小尺度场之和的形式,即

式中微尺度的修正项A(x,ξ)是任意矢量场,适用于有旋场和有散场都存在的情况。将式(3)代入式(2)得到

根据多尺度问题的复合求导运算规则,有

式中,a是人工电磁材料的周期结构边长。利用式(5),考虑非导磁材料,式(4)可以简化为

由于大尺度场一阶近似方程为
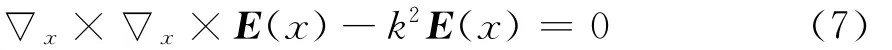
式(6)可以简化为
整体来说,全面深化改革是在“依宪治国”、建设法治国家的大背景下进行的,在改革和法治叠加、相互促进的状态下,改革已具有被自觉地全程纳入法治框架内的意识,并取得了初步成效。在改革和法治进程中,虽然也存在一些“违宪瑕疵”,但在“摸着石头过河”的改革探索阶段,改革与法治存在某种程度的冲突现象具有必然性,而随着改革与法治的进一步交融、交汇,则应强化改革的理性自觉,突出法治在促进改革中的保障作用。所以,我们应重视在改革中寻找问题,不断完善宪法体系,增强宪法的适应性。

用矢量权函数w与式(6)在空间周期单元做内积,得到

定义

得到关于A的微尺度泛函方程

根据方程(9)获得微尺度解,可以将人工介质中总场解写为

方程(6)对周期单元积分取平均,得到的均匀场方程为



从以上公式可以看到,平均场的有效介电常数由两部分组成:第一部分由背景材料和掺杂物材料的介电常数构成;第二部分由矢量场修正项构成,该修正项与频率有关。
2 计算结果与分析
考虑周期为1cm的人工电磁材料,每个周期中包含一个边长为5mm、相对介电常数为10的立方体,背景为空气,相对介电常数为1.假设平面波入射到含周期结构的复合材料上,入射波方向朝正z方向传播,电磁波的频率为1GHz.对于周期结构材料,可以利用周期边界条件求解,计算模型如图1所示。

图1 传播方向有5个周期单元的复合材料结构
对于图1所示的周期结构,采用多尺度有限元方法进行计算,然后与普通有限元方法计算结果作比较。
多尺度有限元的计算分为以下几个步骤:利用式(9)和周期边界条件对单个周期单元进行微尺度计算,得到微尺度周期单元的修正场和有效介电常数;然后,利用有效介电常数对均匀结构进行大尺度计算;将大尺度与微尺度解合成得到复合材料结构总的场分布。图2给出了采用有限元求解微尺度方程(9),得到微尺度的修正电场x分量电场分布的结果,其中相应的有效介电常数为1.374 82.
将该有效介电常数代入到方程(12),可以得到总平均场,该平均场与微尺度场叠加得到总场分布。图3给出了沿着复合材料结构中心线场分布的结果。其中实部与虚部结果都与普通有限元结果进行了比较,两者符合较好,证明所提出的方程可以用于复合材料结构的求解。图4给出了有效介电常数随微尺度结构尺寸的变化,可以看到,随着结构尺度的增加,有效介电常数相应增加。

3 结 论
本文在文献[6-7]研究工作的基础上,针对微小尺度的修正项函数进行了研究。文献[6-7]所用的微小尺度修正项函数是标势函数的梯度,该函数是无旋向量场。对于人工电磁材料的研究而言,该修正项只能说明准静态场对等效电磁参数的贡献,而不能说明有旋场的贡献。针对这个问题,本文给出了一种考虑有旋场贡献的矢量修正项,并得到了一种新的关于微尺度的微分方程。该方程可以包含有旋场对有效电磁参数的影响,比原方程具有更广的使用范围。为了验证方程的有效性,利用基于矢量棱边单元的有限元方法计算了复合材料的多尺度问题,与一般细分网格的有限元方法进行了比较,两种方法得到的结果符合较好,说明了该方法的有效性。
[1]逯贵祯,周 灏,林金才,等.散射参数反演材料电磁参数的新方法[J].电波科学学报,2009,24(2):378-381.LU Guizhen,ZHOU Hao,LIN Jincai,et al.New method of determining permittivity and permeability by scattering coefficients[J].Chinese Journal of Radio Science,2009,24(2):378-381.(in Chinese)
[2]BENSOUSSAN A,LIONS J L,PAPANICOLAOU G.Asymptotic Analysis for Periodic Structures[M].Amsterdam:Elsevier,1978.
[3]ZENG Dongdong,LI Yanfei,LU Guizhen.Study on multi-scale finite element method for EM wave equation[C]//Proceedings of the International Conference on Applications of Electromagnetism and Student Innovation Competition Awards.Taipei,August 11-13,2010:19-23.
[4]LI Cuiyu,ZHANG Xiaotao.Numerical simulation of knitted fabric material with multi-scale finite element method[C]//2009International Conference on Machine Learning and Cybernetics.Baoding,July 12-15,2009,4:2123-2126.
[5]CAO Liqun,ZHANG Ya,ALLEGRETTO W.Multiscale Asymptotic method for Maxwell's equations in composite materials[J].SIAM J Numer Anal,2010,47(6):4257-4289.
[6]OUCHETTO O.Modeling of 3-D periodic multiphase composites by homogenization[J].IEEE MTT,2006,54(6):2615-2619.
[7]OUCHETTO O.Homogenization of 3-D periodic bianisotropic metamaterials[J].IEEE MTT,2006,54(11):3893-3896.
[8]冯永平,崔俊芝,邓明香.周期孔洞区域中热力耦合问题的双尺度有限元计算[J].物理学报,2009,58(S1):327-337.FENG Yongping,CUI Junzhi,DENG Mingxiang.The two-scale finite element computation for thermoelastic problem in periodic perforated domain[J].Acta Physica Sinica,2009,58(S1):327-337.(in Chinese)
[9]LEVY O,STROUD D.Maxwell Garnett theory for mixtures of anisotropic inclusions:application to conducting polymers[J].Physical Review B,1997,56(3):8035-8046.
