单值化处理长江中游主要断面水位流量关系研究

万凤鸣，龙立华，张 悦

单值化处理长江中游主要断面水位流量关系研究

万凤鸣1，2，龙立华3，张 悦3

（1.湖北工业大学商贸学院，武汉 430079；2.武汉理工大学，武汉 430070；3.湖北水利水电职业技术学院，武汉 430202）

为更好地开展长江中游防洪影响的研究，在分析沙市、螺山、汉口3个控制站水文断面水位流量关系影响因素的基础上，选取1981—2010年长江中游沙市、螺山、汉口3个控制站主要断面洪水期（5—9月）的水位流量资料，采用综合落差法进行单值化处理，得到了各站水位流量关系曲线成果，并用最小二乘法原理进行曲线的拟合，对其进行了合理性分析。结果表明，通过多项式拟合能将计算出的水位－流量关系线的影响消除到最小。并且由数学公式计算的关系线推出的流量不会因人为定线的差异而导致数据的不同，在实际应用中，效果更好。

水位流量关系；单值化；多项式拟合

长江流域是我国洪灾多发区，特别是长江中下游平原区12.6万km2，洪灾频繁而严重，1998年的洪水以及近年来严峻的防洪形势，进一步暴露了长江中游防洪存在的问题。因此，很有必要开展长江中游防洪影响的研究［1］。为适应长江河流的动态变化进程，同时遵循水文资料采集的基本原则，本研究采用了上世纪末和本世纪初的实测资料，即1981—2010年长江中游主要断面洪水期（5—9月份）的逐日平均水位、流量数据，用综合落差指数法进行分析计算，得到沙市、螺山、汉口3个控制站的水位流量关系曲线，通过分析了解测站特性，探求其变化规律，以便预估其未来发展趋势。

1 各站水位流量关系的影响因素

1.1 沙市站

沙市水位站下距新厂站67.4 km，距藕池口76.1 km，距城陵矶241.9 km（裁弯前为324.7 km）。沙市—新厂河段既无支流汇入，也无溃口分流，洪水经河道调蓄后坦化作用轻微。

1967—1972年下荆江裁弯引起本站水位流量关系发生系统变化，根据荆江河段的河道特征、洪水组成以及断面分析，认为沙市站的水位流量关系主要受以下因素的影响：断面冲淤变化、城陵矶水位、下游变动回水顶托和洪水涨落率等，其中沙市站的断面水位－面积关系是首要因素［2］。除上述主要因素外，还有荆江与洞庭湖洪水的组成、连续洪水、洪水起涨水位的高低、洪峰的胖瘦等。

1.2 螺山站

螺山水文站上距洞庭湖出口3.5 km，是洞庭湖出流与荆江来水的控制站。下游35 km有陆水河在陆溪口汇入长江，下游约210 km有长江的最大支流汉江在武汉市入汇，同时下游还有金水、滠水、倒水、举水、富水、讳源口、巴水、浠水、圻水等支流对其顶托，这些支流的涨落对螺山站的水位流量有一定影响［3］。

根据城陵矶—汉口河段的自然特征、洪水组成特性以及莲花塘站断面水位－面积关系、水位－流量关系绳套曲线分析，发现影响螺山水位流量关系的因素较为复杂，主要包括断面冲淤变化、河段冲淤变化、下游变动回水顶托、洪水涨落影响等，其次干支流洪水地区组成及江湖关系的演变等对水位流量关系变化也有一定的影响。

1.3 汉口站

汉口站上游约1.4 km处有汉江从左岸入汇，再上游有东荆河、金水和陆水入汇；其下游约9.2 km左岸有府环河入汇，再下游左岸有倒、举、巴、浠、圻等水、武湖及张渡湖入汇，右岸有梁子湖、富水等来汇，下游约284 km有鄱阳湖水系于湖口入汇，下游支流来水对本站水位流量关系有一定顶托的影响。

影响汉口站水位流量关系的主要因素有：下游支流变动回水顶托、洪水涨落、断面冲淤变化，以及干支流洪水遭遇、连续多峰洪水、分洪溃口等特殊水情。

2 水位流量关系曲线拟定的计算原理及方法

近年来在水位流量关系的确定方面，已有大量的研究，提出了综合单位线法、起涨水位法、落差指数法、下游水位参数法等多种计算方法。传统的水位－流量关系曲线的建立一直采用临时曲线法，但此种定线方法受人为因素较多，由于实际工作经验的差异，考虑各项参数的不同，各项参数无法定量，致使不同的人定出的关系曲线不尽相同，据以推算出的流量相互存在差值，在实际工作中造成诸多不便。而通过适当的数学模型来拟合曲线，即可解决此问题［4］。

本文在前人的研究基础之上，按实际情况，在对沙市、螺山、汉口站1981—2010年的洪水期（5—9月份）每日8∶00的水位、流量进行统计分析的基础上，用最小二乘法原理进行曲线的拟合，由于采用多项式，使个别测验误差较大的测点，对计算出的水位－流量关系线的影响消除到最小。因是用数学公式计算的关系线，由关系线推出的流量不会因人为定线的差异而导致数据的不同。在实际应用中，效果更好。

2.1 沙市站

沙市水位流量关系受洪水涨落和莲花塘水位、洞庭湖出水等变动回水顶托影响，因此，90年代的沙市水位流量关系的拟定着重考虑这些因素。

2.1.1 洪水涨落影响改正

由于上述因素的影响，实测流量点据有时呈逆时针绳套曲线，有时点据极为散乱，2种因素混合在一起。为区分这2种影响因素，先根据长江干流洪水较大、洞庭湖来水较小、顶托影响不明显的情况［5］，对1981，1987，1989年资料进行分析，并采用校正因素法对洪水涨落进行修正，上述3年洪水呈明显的绳套曲线，当校正因子取10 000～20 000时，改正效果较好，高水点据明显集中，点群密聚。综合考虑其校正因素1／UIc采用15 000时，效果较好。洪水涨落率改正采用下式进行计算：

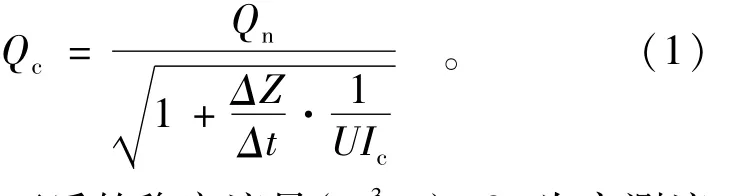
式中：Qc为校正后的稳定流量（m3／s）；Qn为实测流量（m3／s）；Z为洪水的一日上涨或下落水位值（m）；t为时段，取一日等于86 400 s；1／UIc为校正因子，经优选沙市站为15 000。

2.1.2 莲花塘水位顶托的分析

通过对同一时间沙市站和莲花塘实测资料的整编，发现其水位流量关系与莲花塘水位相关，当莲花塘水位较低时，沙市站主要受洪水涨落和断面冲淤影响，水位流量关系点群相对集中；当洞庭湖出流较大，莲花塘水位较高时，沙市站主要受回水顶托影响，水位抬高较多（如1996，1998年），点群分散［6］。

以相应莲花塘水位为参数点绘沙市站1981—2003水位流量测点图，发现原本散乱的点据随莲花塘水位不同而呈现规律性分布，莲花塘水位高的测点在上，水位低的测点在下［7］。我们用下式来分析莲花塘水位的影响，得出沙市站水位流量关系成果（见表1）。

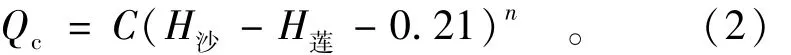
式中：Qc为沙市校正后的稳定流量（m3／s）；C为沙市水位流量关系的相关系数，由实测资料推求；H沙，H莲为沙市、莲花塘水位（m）；0.21为沙市和莲花塘在同一基准面下的高程差（m）；n为应用最小二乘法考虑到H沙与C呈直线关系时求得最小误差时的系数。

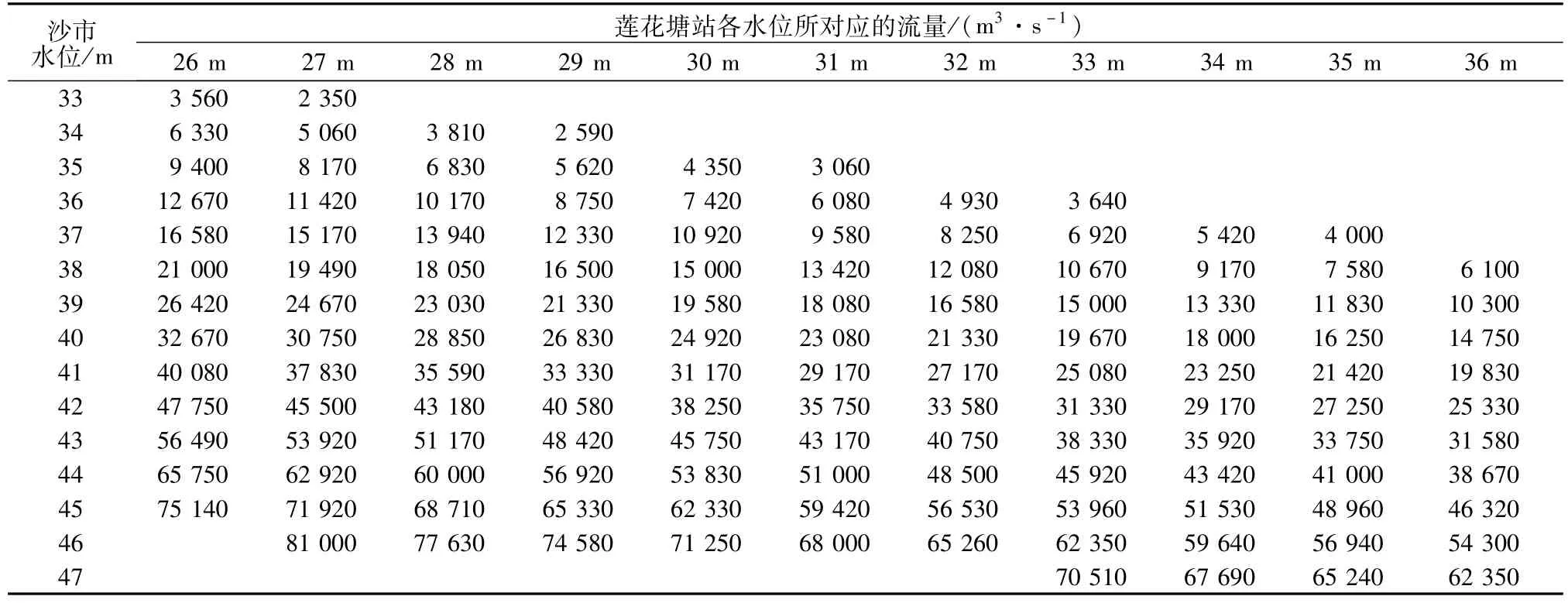
表1 沙市站水位流量关系成果Table 1 The stage-discharge relation at Shashi station

2.2 螺山、汉口站

螺山、汉口站水位流量关系主要受下游支流顶托、洪水涨落等因素影响，下面分别进行分析。

2.2.1 洪水涨落影响改正

受洪水波附加比降作用，螺山站实测水位流量关系受洪水涨落率影响，实测水位流量关系为逆时针绳套曲线。而汉口站水位流量关系受多种因素影响，实测流量资料变幅较大，水位流量关系较为散乱。因此，对受洪水涨落率影响的水位流量关系可采用校正因素法进行改正［8］。经选用1980年以来的中大水年份分析，比较不同的校正因子对水位流量关系绳套线修正效果，各年最优校正因素有一定差异，综合考虑其校正因素1／UIc螺山站、汉口站为40 000效果较好。洪水涨落率改正仍采用式（1）进行计算，其中校正因子1／UIc，经优选为螺山、汉口站取40 000。

2.2.2 下游支流来水的顶托影响改正

螺山站和汉口站下游陆水、金水、汉江、鄂东诸水系和鄱阳湖出流等对螺山及汉口水位有不同程度的顶托影响，各支流来水顶托作用和河槽壅水作用使螺山、汉口站水位抬高［9］。因此，应对其进行顶托影响改正，方法为

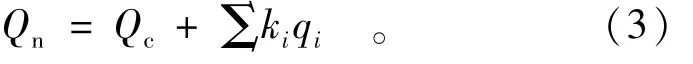
式中：Qn为回水顶托改正后的流量（m3／s）；Qc为经洪水涨落率改正后的流量（m3／s）；qi为螺山—湖口河段各级支流相应顶托流量（m3／s）；ki为支流来水顶托系数（来水取“＋”值，出水取“－”值），ki按1980年9月长江中下游防汛总指挥部《长江中下游防洪基本资料（水情）》取值；i为支流序数。

综合下游支流顶托和洪水涨落这两项主要影响因素，推导出螺山站和汉口站的水位流量，如表2、表3所示。

2.3 多项式拟合方法的原理

由于本次计算数据较多，波动较大，基于多项式拟合方法适用于分析大量数据的偏差，对于数据波动较大时的情况尤为适用。于是运用最小二乘法原理，通过变形回归模型，建立多项式的拟合方程［10］：

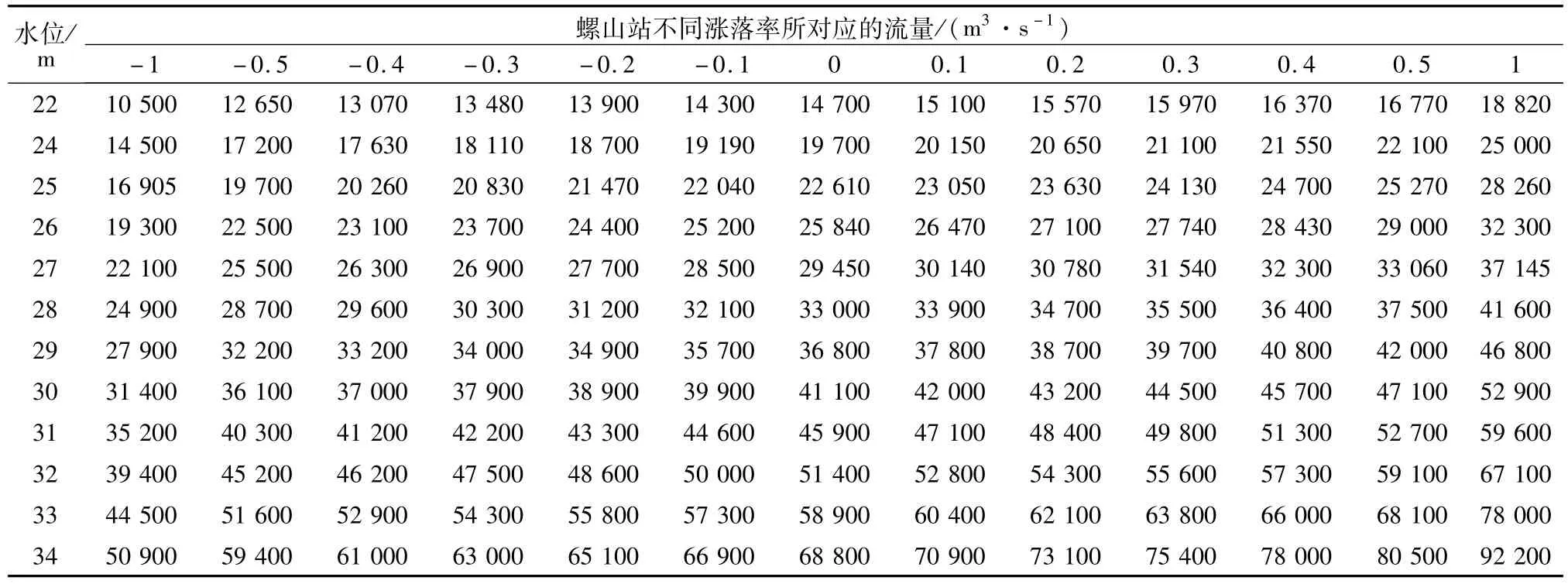
表2 螺山站水位流量关系成果表Table 2 The stage-discharge relation at Luoshan station

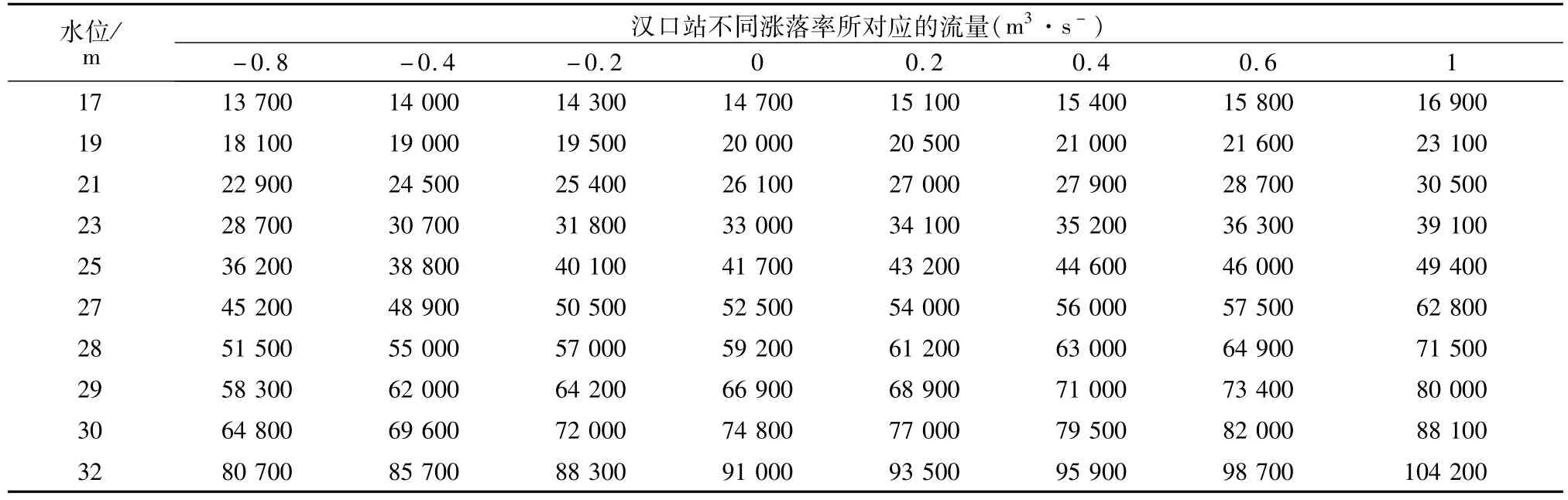
表3 汉口站水位流量关系成果表Table 3 The stage-discharge relation at Hankou station

其中b和ci代表常数。

为了给数据选择最佳的拟合曲线，取参数R2来表征拟合曲线的可靠性。

其中：

当拟合曲线的R平方值等于或接近1时，其可靠性最高。

3 各站水位流量关系曲线成果及合理性分析

3.1 沙市站

本次计算主要采用了1981—2003年的洪水资料，特别是1983，1996，1998，1999与2001年莲花塘34 m以上的高水位资料，能较好地反映现状条件下沙市水位流量关系。我们将沙市实测流量成果，进行洪水涨落率改正和莲花塘水位顶托的分析改正后，最后转换成以莲花塘水位为参数的沙市水位流量关系簇，得到1980—2003年沙市站水文资料拟定的水位流量关系曲线成果（见图1）。

从水位流量关系曲线上可以看出：当莲花塘水位不变时，沙市水位流量关系呈单调递增关系线，沙市流量不变时，沙市水位随莲花塘水位抬高而增高，同一沙市水位，沙市流量随莲花塘水位降低而加大，并趋于稳定。

3.2 螺山、汉口站

如上所述，影响螺山、汉口站水位流量关系因素较多，定量分析全部因素的作用较为困难。因此，针对这2个站主次要影响因素进行分析。采用历年实测水位流量资料，先用校正因素法消除洪水涨落影响，再进行下游回水顶托改正［11］，将各年所定的综合线进行统计分析后得到以涨落率为参数的水位流量关系曲线，见图2、图3。

图1 沙市站水位流量关系曲线Fig.1 Curves of the stage-discharge relation at Shashi station

图2 螺山站水位流量关系曲线Fig.2 Curves of the stage-discharge relation at Luoshan station

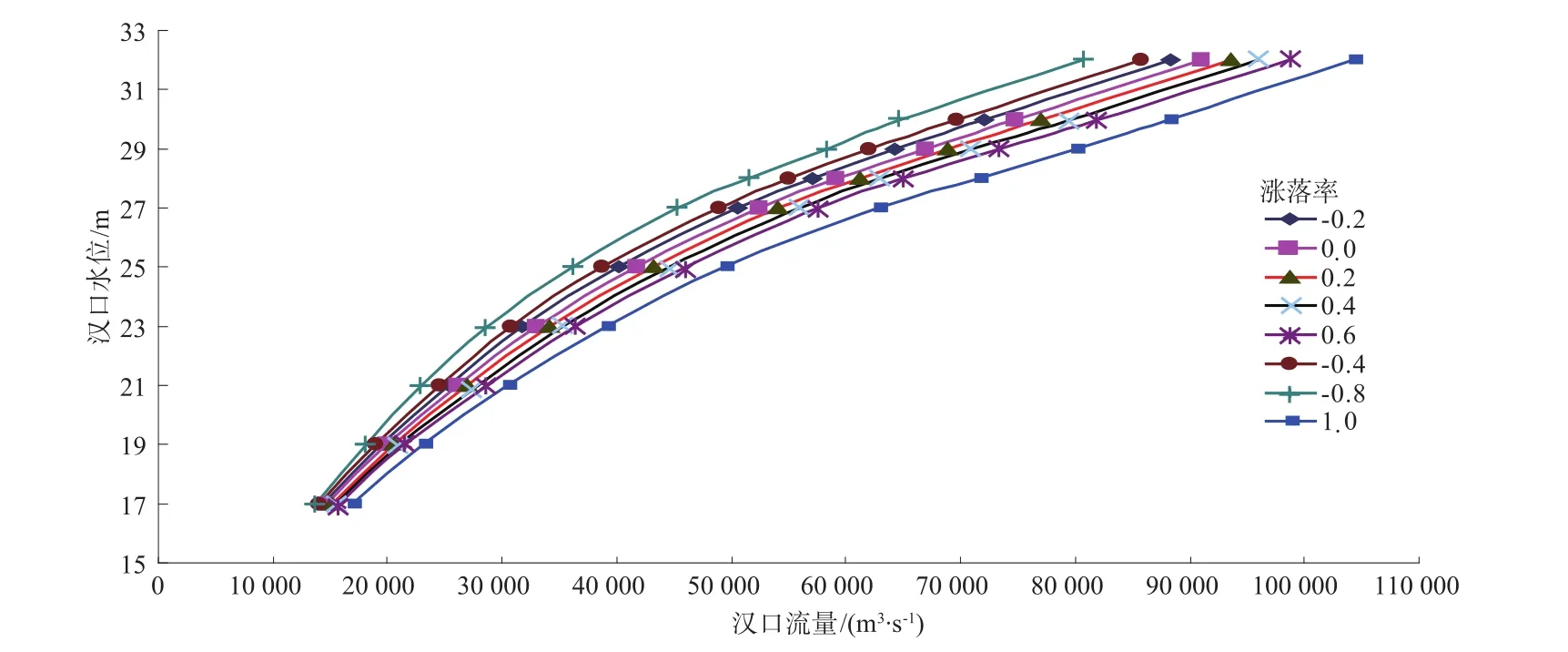
图3 汉口站水位流量关系曲线Fig.3 Curves of the stage-discharge relation at Hankou station

4 结 语

为了检验上述所得各站水位流量关系曲线的合理性，我们选择了1998年的实测数据进行验证计算，具体验证方法为：①根据各控制站实测水位和起涨水位以及相关的参数，由水位流量关系曲线查得Q；②将实测流量过程线与计算流量过程线进行误差统计分析。

分析表明：计算流量与实测流量符合情况较好，所拟定的水位流量关系曲线能较好地吻合1998年实测资料，可见经综合落差法单值化处理求得的水位流量关系是合理可行的。

本研究成果对长江中游水文特性分析，尤其对江湖关系、洪水期水文预报、荆江裁弯河床演变以及超额洪量分配与调度等重大问题均具有重要意义。

［1］ 李世强，邹红梅.长江中游螺山站水位流量关系分析［J］.人民长江，2011，42（6）：87－89.（LI Shi-qiang，ZOU Hong-mei.Analysis onWater Level-Discharge Relation of Luoshan Hydrologic Station in Middle Reaches of Yangtze River［J］.Yangtze River，2011，42（6）：87－89.（in Chinese））

［2］ 吴世勇，刘晓琴，彭艳明.沙市二郎矶站水位流量关系单值化分析研究［J］.人民长江，2010，41（21）：42－44.（WU Shi-yong，LIU Xiao-qin，PENG Yan-ming.A-nalysis and Study for Uniformization of Water Level-Discharge Relation of Erlangji Station on Changjiang［J］.Yangtze River，2010，41（21）：42－44.（in Chinese））

［3］ 施修端.长江螺山汉口大通三站水位流量关系历年变化分析［J］.人民长江，1993，24（7）：43－48.（SHI Xiu-duan.Variation of the Stage-Discharge Curves over Years at Three Yangtze Hydrologic Stations［J］.Yangtze River，1993，24（7）：43－48.（in Chinese））

［4］ 栾震宇，施 勇，陈炼钢.三峡工程蓄水前后长江中游水位流量变化分析［J］.人民长江，2009，40（14）：44－46.（LUAN Zhen-yu，SHI Yong，CHEN Lian-gang.A-nalysis ofWater Level and Discharge Variation in Middle Yangtze River after Impoundment of TGP Reservoir［J］.Yangtze River，2009，40（14）：44－46.（in Chinese））

［5］ 黄诚良.落差指数法在水位流量关系单值化处理中的应用［J］.长江工程职业技术学院学报，2010，27（2）：52－54.（HUANG Cheng-liang.Fall ExponentMethod in Uniformization Treatment of Water Level and Flow Relation［J］.Journal of Changjiang Engineering Vocational College，2010，27（2）：52－54.（in Chinese））

［6］ 谢作涛，张小峰，谈广鸣.长江螺山站水位流量绳套曲线关系预报研究［J］.武汉大学学报（工学版），2005，38（2）：15－19.（XIE Zuo-tao，ZHANG Xiao-feng，TAN Guang-ming.Forecasting of Stage-Discharge Relationship of Luoshan on the Yangtze River［J］.Engineering Journal ofWuhan University，2005，38（2）：15－19.（in Chinese））

［7］ 郭希望，陈剑池，邹 宁.长江中下游主要水文站水位流量关系研究［J］.人民长江，2006，37（9）：68－71.（GUO Xi-wang，CHEN Jian-chi，ZOU Ning.Research on Stage-Discharge Relation of Main Hydrologic Stations on Middle and Lower Reach of the Yangtze River［J］.Yangtze River，2006，37（9）：68－71.（in Chinese））

［8］ 安莉娜，葛守西.用落差指数法将受顶托测站水位转换为流量［J］.人民长江，2003，34（7）：35－37.（AN Li-na，GE Shou-xi.Discharge Calculation from Water Level of Gauging Station Influenced by Backwater with Water-head Index Method［J］.Yangtze River，2003，34（7）：35－37.（in Chinese））

［9］ 谢作涛，张小峰，谈广鸣.长江螺山站水位预报研究［J］.水电能源科学，2003，21（3）：7－9.（XIE Zuo-tao，ZHANG Xiao-feng，TAN Guang-ming.Forecasting ofWater Level of Luoshan Station in Yangtze River［J］.Water Resource and Power，2003，21（3）：7－9.（in Chinese））［10］巢中根，李正最.水位流量关系分析中落差指数的直接解算［J］.水文，2000，20（3）：18－20.（CHAO Zhong-gen，LIZheng-zui.The Direct Solution of Fall Exponent in Stage-Discharge Relationship Analysis［J］.Hydrology，2000，20（3）：18－20.（in Chinese））

［11 DAIQing.Application of a New Method in Studying the Scattered Stage-Discharge Relationship of Unsteady Flows［J］.International Journal of Sediment Research，2001，16（2）：301－307.

（编辑：赵卫兵）

Single Valued Processing of Stage-Discharge Relation in the M ain Cross Section of M iddle Reaches of Yangtze River

WAN Feng-ming1，2，LONG Li-hua3，ZHANG Yue3
（1.Business School，Hubei University of Technology，Wuhan 430079，China；2.Wuhan University of Technology，Wuhan 430070，China；3.HubeiWater Resources Technical College，Wuhan 430202，China）

To better research the flood control impact on themiddle Yangtze River，we analyzed the factors affecting the stage-discharge relation in the cross-sections at three hydrological stations，namely，Shashi，Luoshan，and Hankou Station.Furthermore，on the basis of the measured data of water level and flow during flood season（May-September）from 1981 to 2010，single valued processing is employed to obtain the stage-discharge relation curves，which are further fitted in accordance with the principle of least squares.Results indicate that the impact of stagedischarge curve can be eliminated to aminimum through the polynomial fitting，and the flow deduced from the relation curve calculated by mathematical formulas will be free from inconsistency caused by human objectivity.In practical application，the effect is better.

stage-discharge relationship；single valued；polynomial fitting

P332.4

A

1001－5485（2012）12－0005－05

10.3969／j.issn.1001－5485.2012.12.002 2012，29（12）：5－9，33

2011－10－12；

2012－06－13

万凤鸣（1982－），女，湖北松滋人，讲师，博士研究生，主要从事岩土工程研究，（电话）13437119588（电子信箱）564017119＠qq.com。