腔体形状对混响室内场均匀性的影响

李 爽 王建国，2 谢海燕 陆希成

（1.西北核技术研究所，陕西 西安 710024；2.西安交通大学电子与信息工程学院，陕西 西安710049）

引 言

随着高功率微波（HPM）技术的快速发展［1］，现代武器系统所处的电磁环境更趋复杂，这给武器装备的安全性构成了严重威胁。因此，有必要对各类武器系统进行HPM辐照效应研究。通常对武器系统进行HPM效应研究，可以利用外场或者微波暗室来进行，相关研究也都取得了丰富的成果。但为了得到统计规律，这种试验方法需要的统计样本较多，试验成本较为昂贵，实施也比较复杂。同时，整系统的效应规律与其内部子系统的效应特征也密切相关。对于复杂腔体中的子系统设备，所处的电磁环境更为复杂。外部HPM可以通过多种耦合途径（天线、腔体上的孔缝等）进入腔体内部，对腔体内的子系统设备产生影响，从而严重影响整系统的工作效能。因此，开展对复杂腔体内子系统的HPM效应研究也是十分必要的。而传统试验场地也难以模拟这种复杂的电磁环境。这给研究复杂腔体内子系统的HPM效应带来了很大的困难。

混响室作为一种新型电磁效应试验设备，能够在腔体内产生统计意义上的各向同性均匀场，可以很好地模拟复杂电磁环境，因而对研究复杂腔体内部子系统的电磁效应具有重要意义［2－5］。美国的Crawford等对混响室的结构设计、性能评价方面进行了一系列的试验和研究［6］；1992年英国的Huang教授首次提出了源搅拌混响室的概念［7］。国内方面，北京邮电大学的高攸纲、沈远茂［8－9］以及买望［10］等人均在混响室设计及均匀性分析方面做了大量工作。然而，目前的混响室研究主要是基于连续波激励，很少有涉及脉冲波激励下的混响室特性研究。本文将从理论分析和数值模拟两个方面，研究HPM激励下，不同的腔体形状对腔内电磁场分布的影响，为该型混响室的设计提供技术参考。

1.理论分析

1.1 混响室的搅拌原理

实际应用中的混响室，一般是通过其内部的源天线激励，构造电磁场环境，这相当于一个有源谐振腔。研究混响室内的搅拌原理，可以借助有源谐振腔内部的电磁场理论进行分析。下面以简单的二维有源矩形谐振腔为例进行研究，如图1所示。

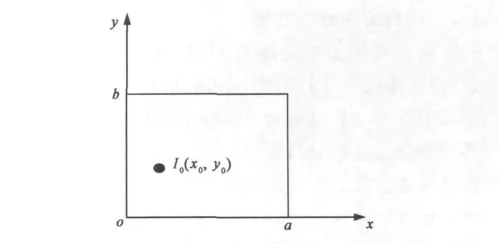
图1 二维有源谐振腔

腔体放置在xOy平面上，边长分别为a和b，腔体材料为理想导体，其他区域均为自由空间。激励源是沿z轴放置的电振子（I0），位置在（x0，y0）.腔体内部的非零电场分量Ez可以表示为［8］

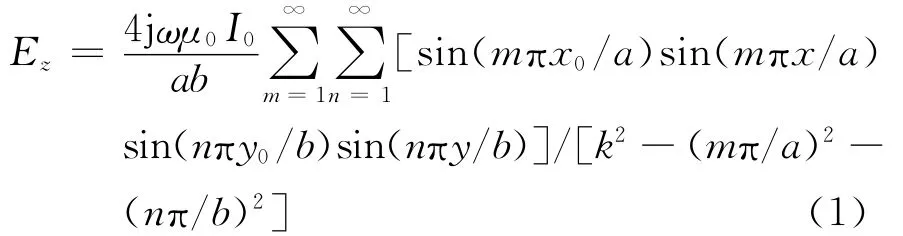
式中：k2＝ω2με.二维模型中的谐振频率为

式中：m、n分别表示x、y方向的半波数；a、b分别为矩形腔体的长、宽。

从式（1）可以看出：在空间介质不变的情况下，腔体内的场分布取决于以下因素：①腔体的形状、尺寸；②激励源的位置、幅度等。

传统的混响室是根据因素①，在腔体内设置机械搅拌器来实现搅拌功能的。当搅拌器进行旋转时，即可以不断地改变腔内的边界条件，进而改变腔体内模式的谐振状态，从而实现混响室所要求的统计均匀场。

源搅拌混响室是根据因素②来工作的［11－12］。通过对激励源的扰动来影响有效模式组合中各模式所占的权重，进而对腔体内的场分布产生搅动效果。

根据微波混沌理论，复杂腔体不同于规则腔体，其内部电磁波的传播一般具有复杂性和非周期性，除了一些特殊方向的射线能够产生规则轨道之外，在大部分情况下它们都将产生复杂的不规则轨道。而且空腔中规则的短周期轨道具有强烈的不稳定性，会对本征函数造成“疤痕”现象［13］。腔体内电磁波分布的复杂度对电磁场分布的统计均匀性有重要影响。而在腔体尺寸一定的情况下（参数a、b保持大致不变），改变腔体内部的细微结构，可以改变腔体内部场的边界条件，进而影响场分布的状态。因此，腔体形状对腔内场分布状态具有重要的影响。

重点研究HPM激励下的混响室，由于脉冲持续时间短，远小于机械搅拌中机械臂运动的特征时间，而且腔内场的瞬态特性强，难以在腔体内形成类似连续波那样的稳定状态。因此，机械搅拌的方法不适于用HPM效应分析的混响室。这里考虑采用源搅拌方法，通过多天线激励的方式来实现对腔体内电场的搅拌，以此为基础，在相同搅拌条件下研究腔体形状对场分布的影响。

1.2 场均匀性分析方法

由于混响室中的场均匀性是统计意义上的概念，需要借助统计计算方法来验证场的均匀性。根据IEC 61000－4－21标准［14］，对于稳态场的混响室校准，是在测试区域的顶点处放置8个电场探头，搅拌器以步进方式旋转一圈，每个步进位置为一个采样点。在每个采样点上，用8个探头测量各个位置三个正交方向的电场强度。用所有采样点场值的标准差来反映场的空间均匀性。但是在脉冲波激励下，有耗腔体内的场随时间剧烈变化，难以形成稳定状态。本文重点关注脉冲波对器件的电磁瞬态效应，所以，不能像稳态场那样只考虑场的空间均匀性，还要关注场的时域特性。在本文中，主要参考IEC 61000－4－21，观测一段时间内整个测试区域内的场值，分析电场随时间的变化特征，并选取若干平面来分析场分布的空间均匀性。场值分布的标准差越小则说明场值分布越均匀，因而也就越有利于在腔体内对器件进行相关的瞬态效应实验。

为观测腔体内瞬态电场的时域特性，选取一定长度的时间窗口作为研究单元。在每个时间窗内，观测整个测量空间内每个场点的电场最大值，综合所有的场点，分析整个空间内的最大值及场值分布标准差，可以得到该时间窗内腔体中的电场分布特征。综合若干个时间窗，还可以得到腔体内电场的时域分布特征。由此，可以得到不同条件下电场的空间分布特征，总结出改善场分布均匀性的规律。具体的统计计算过程如下：

腔体内某测试点（xi，yi，zi）在时刻点t1的电场表示为

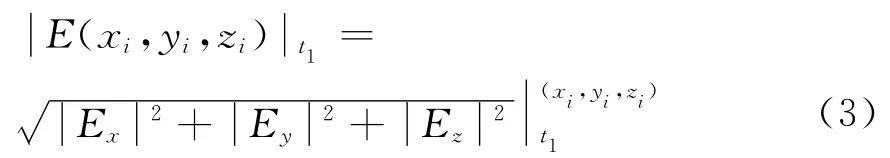
该测试点在某个时间窗Tj（时刻t1到tp）内的电场最大值为

单方向上的平均值 〈Eξ〉（ξ＝x，y，z）和3个方向的联合平均值〈Exyz〉可以分别定义为

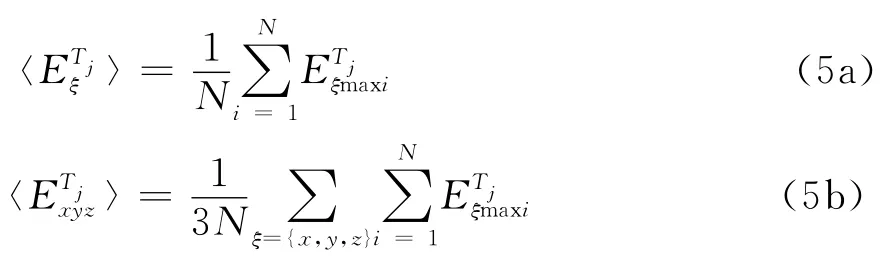
式中，N为单方向上观测的场点个数。

单方向上的标准差σξ和3个方向的联合标准差σxyz可以分别定义为

1.3 各向同性

混响室内的电磁场分布具有各向同性的特点，腔内各个方向上的能流密度均衡，便于对受试设备进行全向测试［15］。腔体内电场的各向同性研究，可以通过比较各频点下电场分量的平方值得到。为了避免激励源参数（激励幅度等）对该分布的影响，主要研究各方向上的能流密度占总场能流密度的比值理想情况下，三个比值均应为1/3.

2.数值计算

2.1 数值计算模型

主要计算并对比矩形腔体、复杂腔［16］（在腔体内壁上引入若干半球形金属凸起结构，凸起结构的半径约为1倍波长）、凹形腔（凹去部分尺寸为2倍波长）等形状腔体内的场分布形式。其中，矩形腔代表的是规则腔体，复杂腔是根据声学混响室中的返波体引申得到的形状，可以增加腔体内电磁波的反射方向，而凹形腔是电磁统计学中典型的Sinai腔模型。研究的腔体尺寸均约为6倍波长，具体形状如图2所示。在腔内均采用载频3GHz，脉宽10ns的脉冲波进行激励。

对于每种模型，首先采用时域有限差分（FDTD）方法分析整个腔体内电场的时域分布特征［17］，得到场分布结果；在场值最大的时间窗内，进一步分析腔内不同平面上的电场分布。选取两个z平面进行研究，其中z1面靠近腔壁，z2面位于腔体中央。整个时域研究长度选取为10个时间窗Ti（i＝0，1，2，……，9），其中T0代表天线开始进行激励的时间窗，时间窗的长度选取与脉宽相同。还分析了腔内电场的各向同性分布。

2.2 数值计算结果

2.2.1 整个空间内电场的时域分布特点

根据图3（a）可以看出：复杂腔、矩形腔和凹形腔在T1、T2时间窗内，腔内电场值达到最大，随后场值逐渐衰减。这两个时间段是进行瞬态效应研究的重点关注区域。根据图3（b），复杂腔和凹形腔在T1和T2内的场均匀性都比矩形腔好。这是由于加入了复杂结构，增加了电磁波的反射方向，而各场点上的电场是直射、反射电磁波的叠加，所以，各场点的场值更接近。该结果表明：在矩形腔结构的基础上引入若干复杂结构，可以有效地改善腔体内的电场分布，提高场分布的均匀性。不过，凹形腔的特殊结构会造成腔内测量空间的减小，影响实际应用范围。

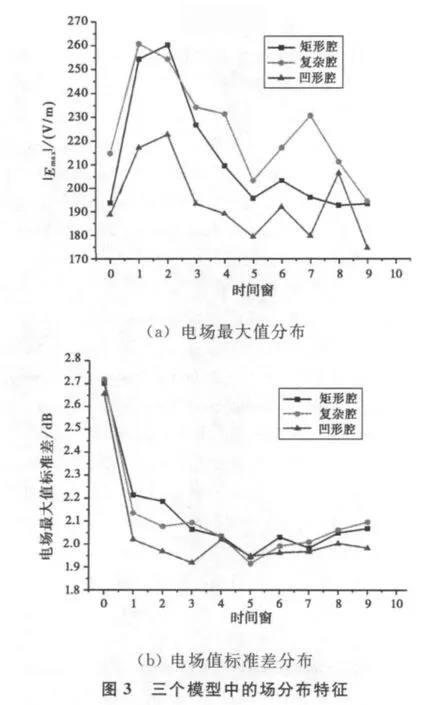
2.2.2 平面上电磁场的分布特点

从电场的时域分布图可以看出，在腔体内激励刚完成的时刻，即T1、T2时间窗内，腔体内的电场值最大。因此，这两个时间窗是我们开展电磁效应研究的重点，选取T1下z1和z2两个面来研究腔体内部不同位置处的场分布特征，具体结果见图4所示。

从图4可以看出：复杂腔中的场分布更加均匀，整个平面上的电场值相差不大。而且，平面z2比平面z1的场分布要更加均匀。而其他两种模型中，场值的空间分布变化较大，统计均匀性不如复杂腔。这说明在复杂腔内电场的分布更加均匀，采用该种腔形可以很好地改善腔内场分布的均匀性。由于腔壁表面电流的影响，腔内中央处的场均匀性也比靠近腔壁处的好。所以，采用类似复杂腔的结构，在矩形腔的基础上引入若干复杂结构，可以增加腔内电磁波的反射，更有利于在腔内构造均匀的电磁环境。

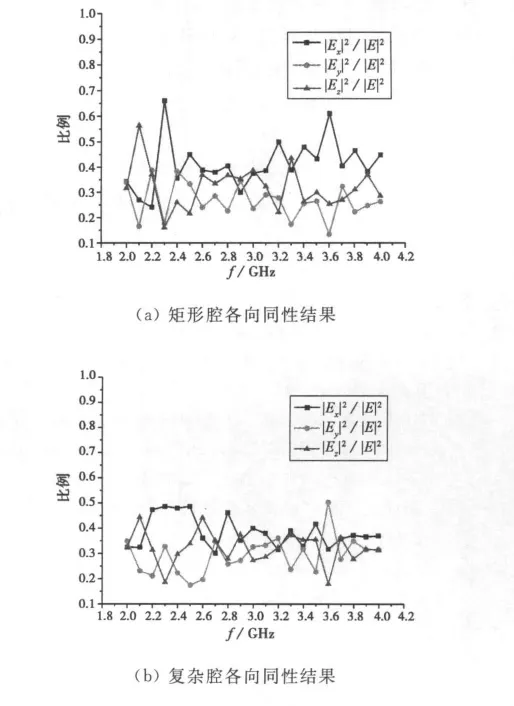
2.2.3 各向同性

混响室的特征之一就是具有良好的各向同性，即各方向上的能流密度均衡，能够对被测设备进行全向均匀测试。从图5可以明显看出，复杂腔和凹形腔比矩形腔内的能流分布更均衡。而且频率越高，各方向上的能量分布就越均衡。因此，利用混响室技术对器件进行辐照试验时，可以实现对器件的全向辐照，不需要每辐照一个方向就移动一次天线。

图5 不同模型中的各向同性结果

3.结 论

通过采用源搅拌的方法，研究了在HPM激励下腔体形状对腔体内电场分布的影响效果。首先通过谐振腔理论和微波混沌理论的分析，证明腔体形状对腔体内的场分布有重要影响。其次，以多天线激励为基础，通过数值模拟计算验证腔体形状对腔内场分布的影响。结果表明：在矩形腔的基础上引入一定的复杂结构，可以增强腔内电磁波的反射效果，增加腔内电磁场的复杂度，有效地提高场分布的均匀性及能量的均衡性，对构造HPM下的混响室有重要意义。但是，也要注意引入复杂结构后对腔体带来的其他影响，如本文中的凹形腔体会影响腔内的实际测量空间。同时，由于目前混响室实验室还处于搭建阶段，相关验证实验尚未能进行。开展相关实验，对理论结果进行验证也是下一步的工作重点。

［1］BENFORD J，SWEGLE J，SCHAMILOGLU E.High Power Microwaves［M］.2nd ed.New York：CRC Press，2007：35－37.

［2］HILL D A.Electronic mode stirring for reverberation chamber［J］.IEEE Transactions on Electromagnetic Compatibility，1994，36（4）：294－299.

［3］张林昌.混响室及其进展［J］.安全与电磁兼容，2001，（1）：2－8.ZHANG Linchang.The development of reverberation studio［J］.Safety and EMC，2001，（1）：2－8.（in Chinese）

［4］GRADONI G，ARNAUT L R.Generalized extreme－value distributions of power near a boundary inside electromagnetic reverberation chamber ［J］.IEEE Transactions on Electromagnetic Compatibility，2010，52（3）：506－515.

［5］BACKSTROM M G，LOVSTRAND K G.Susceptibility of electronic systems to high－power microwaves：summary of test experience［J］.IEEE Transactions on Electromagnetic Compatibility，2004，46（3）：396－403.

［6］CRAWFORD M L，KOEPKE G H.Design，Evaluation，and Use of a Reverberation Chamber for Performing Electromagnetic Susceptibility/Vulnerability Measurements［S］.Washington：US Department of commerence，National Bureau of standards 1986.

［7］HUANG Y，EDWARDS D J.A novel reverberating chamber：the source－stirred chamber［C］//8th International Conference on Electromagnetic Compatibility.Oxford，UK，1992：120－124.

［8］沈远茂，高攸刚.电磁兼容测试中的源搅拌混响室和电磁干扰接收机的相关研究［D］.北京：北京邮电大学，2006.SHEN Yuanmao，GAO Yougang.Research about Source－Stirred Reverberation Chamber and Electromagnetic Interference Measuring Receiver in the Field of Electromagnetic Compatibility Tests［D］.Beijing：Beijing University of posts and telecommunications，2006.（in Chinese）

［9］沈远茂，石 丹，高攸纲，等.利用多天线源搅拌改善混响室场均匀性的分析［J］.电波科学学报，2009，24（4）：682－686.SHEN Yuanmao，SHI Dan，GAO Yougang，et al.Improvement in field uniformity introduced by multiple－antenna in source－stirred reverberation chamber［J］.Chinese Journal of Radio Science，2009，24（4）：682－686.（in Chinese）

［10］买 望，高攸纲.混响室场均匀性的仿真与分析［D］.北京：北京邮电大学，2006.MAI Wang，GAO Yougang.Simulation and Analyzation of Uniformity inside Reverberation Chamber［D］.Beijing：Beijing University of posts and telecommunications，2006.（in Chinese）

［11］CERRI G，MARIANI V，PENNSI S，et al.Source Stirring Mode for Reverberation Chambers［J］.IEEE Transactions on Electromagnetic Compatibility，2005，47（4）：815－823.

［12］梁双港，许家栋，刘易勇，等.源搅拌混响室的仿真分析与实验研究［J］.电波科学学报，2010，25（6）：1058－1063.LIANG Shuanggang，XU Jiadong，LIU Yiyong，et al.Simulation analysis and experimental investigation of SSRC［J］.Chinese Journal of Radio Science，2010，25（6）：1058－1063.（in Chinese）

［13］陆希成，王建国.复杂腔体电磁耦合效应的统计方法研究［D］.西安：西北核技术研究所，2010.LU Xicheng，WANG Jianguo.Statistical Method Study in Electromagnetic Coupling of Complex Cavities［D］.Xi’an：Norethwest Institute of Nuclear Technology，2010.（in Chinese）

［14］International Electrotechnical Commission.Electromagnetic compatibility （EMC）－Part 4－21：Testing and measurement techniques－reverberation chamber test methods［R］.Geneva：IEC，2003.

［15］HERLEM Y，SCHAFFAR A，GINESTE P N，et al.Oversized cavity limits assessment by numerical simulation［R］.Florence：ESA Workshop on Aerospace EMC，2009.

［16］PETRISCH M，SCHWAB A J.Investigation of the field uniformity of a mode－stirred chamber using diffusers based on acoustic theory［J］.IEEE Transactions on Electromagnetic Compatibility，1999，41（4）：446－451.

［17］黄 华，牛中奇，白 冰.时域有限差分法分析混响室中场的均匀性［J］.电波科学学报，2011，26（1）：124－132.HUANG Hua，NIU Zhong－qi，BAI Bing.Using FDTD to analyze the field uniformity in reverberation chamber［J］.Chinese Journal of Radio Science，2011，26（1）：124－132.（in Chinese）