基于特征参数的随机噪声雷达相关输出研究

武 昕 李 澍 刘 畅 王岩飞

（1.中国科学院电子学研究所，北京100190；2.中国科学院研究生院，北京100039）

引 言

随着电磁环境的日益复杂，提高雷达的抗干扰性能成为了必要。随机噪声雷达［1］是一种具有强抗干扰性的雷达体制，它以微波噪声或噪声调制信号为发射信号。由于发射信号的随机性，它具有优良的低截获概率（LPI）、电磁兼容性（EMC）和电子反对抗性（ECCM）［2－4］。随机噪声雷达已经形成了较完整的理论体系，南京理工大学电子工程技术研究中心取得了大量研究成果，先后成功研制了随机调频连续波雷达系统、正弦加随机调频连续波雷达系统、随机二相码连续波雷达系统等［1－2］。文献［1］对随机噪声雷达的基本原理、典型的随机噪声雷达系统作了深入分析。采用随机噪声信号体制可有效提高雷达在战争环境下的生存能力，其很强的抗干扰能力可以在多种复杂的干扰环境中体现［3－5］。美国内布拉斯加大学环境遥感实验室对噪声雷达的极化和干涉特性进行了研究，并推出了探测掩体目标的新颖超宽带随机噪声连续波雷达系统［6］。噪声雷达的理论和数学模型在不断地更新和完善，近期文献［7－8］提出了信号形式和数字特征会对相关输出造成影响。针对噪声雷达时域相关的特点，文献［9－10］提出了适用于噪声雷达系统的旁瓣抑制方法。随机噪声雷达在成像领域的应用是研究的热点［11］，将其用于合成孔径雷达（SAR）和逆合成孔径雷达（ISAR）成像是重要趋势。同时，与超宽带技术的结合使得噪声雷达具有很强的探测力和穿透力，对障碍物、围墙之后的目标进行检测和成像取得了最新研究成果［12］。

随机噪声雷达通过时域相关完成距离向脉冲压缩，相关输出是脉冲压缩结果。因此，需要建立发射信号的数字特征参数与相关输出之间的联系。随机噪声雷达中同样存在脉冲体制雷达的问题，强目标的旁瓣容易使附近弱目标的主瓣发生畸变，因此降低旁瓣对提高距离向分辨率有重要意义。通过分析随机噪声信号源的相关系数和方差建立了发射信号特征参数与相关输出之间的联系。在相关输出的一般性数学模型基础上，得到了以相关系数和方差为参数的相关输出数学模型，并通过分析和推导得到了重要结论。该结论为随机波形的设计提供了依据，同时为解决旁瓣抑制问题提供了新思路，验证了特征参数的改变能够很好地抑制旁瓣，使分辨率得到很大程度的提高。

1.随机噪声雷达系统与信号处理模型

随机噪声雷达系统通过时域相关来完成脉冲压缩，图1为系统的基本框图。发射信号X（t）经目标反射后产生时延T0（反射系数设为1），由接收天线接收反射信号X（t－T0）；同时，发射信号的另一路分支通过信号延迟线提供变化的时延Tr来产生变化的参考信号X（t－Tr）.将X（t－T0）和X（t－Tr）两路信号进行相关积分，可测得目标的距离和速度信息［7］。

图1 随机信号雷达系统框图

随机噪声信号的复数形式可表示为

式中：ω0为传输信号的中心角频率；XI（t）与XQ（t）是均值为零，带宽为B的高斯过程。目标带有速度信息时，反射信号延时为t的函数，记作T，如式（2）所示。

R0是目标与雷达的最初距离，c为电磁波传播速度。将式（2）代入式（1），则反射信号可表示为

式中α＝1－2ν/c带有目标的速度信息，称作速度因子。参考信号通过延迟线提供变化的时延Tr和变化的速度因子αr与反射信号X（t－T）作相关积分，积分输出的峰值处满足T＝Tr且α＝αr，从而根据R0＝cTr/2和ν＝c（1－αr）/2得到目标的位置和速度。相关积分的数学表达如式（4）所示。

式中TN为相关积分时间。由于XI（·）和XQ（·）服从同一分布，它们的方差和均值相等，从而其自相关函数RI（·）和RQ（·）相等，记作RI（·）＝RQ（·）＝R（·）.相关输出可近似为相关积分的均值，表示为

式中：Δα＝α－αr；ΔT＝T0－Tr；RIQ（·）是XI（·）和XQ（·）的互相关函数，且RIQ（·）＝（·）.由于互相关函数值很小可以忽略，因此，相关输出可简化为

2.基于相关系数和方差的相关输出数学模型

实际中以噪声调制信号作为发射信号的情况更为广泛，并且其相关输出特征更为复杂。以噪声相位调制和频率调制信号为对象进行分析，在式（6）基础上建立依赖于噪声源信号相关系数和方差的相关输出数学模型。

2.1 相位调制信号的相关输出数学模型

经过随机噪声相位调制后的信号复数表达式［7］为

式中，θ（t）是均值为零，方差为的高斯分布随机噪声信号。不失一般性A＝1，其相关输出可表示为

对比式（8）和式（6），R（Δαt－ΔT）即为噪声相位调制信号的自相关函数，其表达式为

依据随机过程理论，均值为零时二维高斯分布的特征函数［13］为

将式（11）代入式（8）即可得到以噪声源信号的相关系数和方差为参数的相关输出表达式，如式（12）所示。

2.2 频率调制信号的相关输出数学模型经过随机噪声频率调制后的信号可表达为［7］

式中，f（x）是均值为零，方差为的高斯分布随机噪声信号。设则式（8）和（9）同样适用于频率调制信号。令Δαt－ΔT＝τ，重写式（9）为

式（14）即为噪声频率调制信号的自相关函数，式中Δθ为 （t′＝αrt－Tr）

由随机过程理论可知，均值为零、方差为σ2的一维高斯分布ξ的特征函数［13］为

对比式（14）与式（16），R（τ）可看作t＝1时一维高斯随机变量Δθ的特征函数，则R（τ）可表示为

式中ρf（τ）是f（x）和f（x－τ）的相关系数。根据方差的定义，并将式（18）代入后用可表示为

将式（19）代入式（17）可得

将式（20）代入式（8），可得到以噪声源信号的相关系数和方差所表达的相关输出表达式，如式（21）所示。

3.相关系数和方差对相关输出和带宽的影响

自相关函数R（τ）决定了相关输出，噪声源信号的相关系数和方差是R（τ）的决定性参数。依据所建立的数学模型分析噪声源信号的相关系数和方差对相关输出及带宽的影响。

3.1 相关系数和方差对相关输出的影响

根据相关系数的定义，ρp（τ）和ρf（τ）可记作

式中Rθ（τ）和Rf（τ）分别为噪声源信号θ（t）和f（x）的自相关函数。

根据式（22）和（23）可知，ρp（τ）和ρf（τ）实质上取决于θ（t）和f（x）的自相关函数。由于信号的方差为常数，相关系数与噪声源信号的自相关函数具有相同的形式。由维纳—辛钦定理［13］可知自相关函数和功率谱函数是傅里叶变换对，随机噪声信号的功率谱函数直接影响相关系数，通过功率谱来分析相关系数对输出的影响。从实用性和普遍性考虑，选择矩形、高斯形和类钟形三种形式的功率谱函数，对应的Rθ（τ）和Rf（τ）分别为sinc函数、高斯函数和双边指数函数。相关系数也具有这三种函数形式。将具体的相关系数代入式（11）和（20），可得到自相关函数R（τ）的表达式，如表1所示。

表1 取三种相关系数时调制信号的自相关函数R（τ）

相关系数决定了R（τ）的函数形式，从而决定了相关输出的主瓣能量分布和旁瓣水平。当噪声源信号为矩形功率谱时，相关系数为sinc函数，输出有明显的旁瓣，并且具有一定周期性。当相关系数为高斯函数时，没有明显的旁瓣，但主峰不尖锐，主瓣较宽。当相关系数为双边指数时，没有明显的旁瓣，且主峰尖锐，能量集中。仿真实验可以对该结论进行验证。

分析方差对相关输出的影响。衡量脉冲压缩性能的两个重要指标是峰值旁瓣比 （PSLR）和积分旁瓣比 （ISLR），它们的定义为

式中：Rside和Rmain分别为旁瓣高度和主瓣高度；Ptotal为总功率；Pmain为主瓣功率。

以ρp（τ）取sinc（πBτ）的相位调制信号为例进行分析，B为噪声信号θ（t）的带宽。式（11）决定了相位调制信号的相关输出，对式（11）求一阶导数可得

B为带宽是定值，根据式（26）可知式（11）的极值点是固定点，不随方差而变化。旁瓣高度为R（τ）某一极值点的函数值，它只随方差的变化而变化。根据式（11），R（τ）是关于方差的减函数，因此随着方差的增大旁瓣高度会减小。在不同的方差下式（11）具有相同的极限最大值，如式（27）所示。

max｛R（τ）｝可看作主瓣高度，因此，PSLR是方差的减函数，随着方差的增大PSLR减小，指标性能得到提高。方差的增大同样使ISLR减小，在仿真结果中可得到验证，在此不作出数学分析。

表2为不同方差下，ρp（τ）为sinc（πBτ）时R（τ）的PSLR和ISLR，反映出随着方差的增大，两项指标值大幅减小，指标性能得到提高。同样，该结论适用于相关系数为其它形式的情况及频率调制信号。

表2 不同方差下R（τ）的两项指标/dB

图2所示为不同方差下R（τ）的输出。图2（a）和图2（b）分别为ρp（τ）＝sinc（πBτ）和ρp（τ）＝exp（－｜τ｜/τ0）时相位调制信号的R（τ）输出。图2（c）为ρf（τ）＝exp（－｜τ｜/τ0）时频率调制信号的R（τ）输出。图2（c）中取方差与时间常数τ0乘积的变化。因为时间常数为定值，方差与时间常数乘积的变化等价于方差的变化。从图2（a）和（b）可以看出，随着方差的增大，旁瓣水平明显降低，主瓣变窄变尖锐。图2（c）同样可反映出方差的增大使主瓣变尖锐，分辨率得到很大程度的提高。主峰和旁瓣的形式取决于相关系数的形式，同时与调制方式有关。方差对相关输出的影响主要表现在对R（τ）的影响上。

噪声源信号的相关系数决定了相关输出的形式和旁瓣水平，方差对分辨率的提高和旁瓣的抑制起到重要作用。

3.2 相关系数和方差对带宽的影响

随机信号的方差反映了信号偏离总体均值的程度，方差越大说明信号的波动和起伏越大，因此所需的带宽越大。下面利用数学推导证明该观点。

发射信号的带宽定义为［7］

式中S（f）为发射信号的功率谱。自相关函数R（τ）为S（f）的傅里叶逆变换，如式（29）所示。

对式（29）求二阶导数为

综合式（28）～（30）可得

分别对式（11）和（20）求二阶导数，可得到相位调制信号和频率调制信号自相关函数R（τ）的二阶导数，如式（32）和（33）所示。

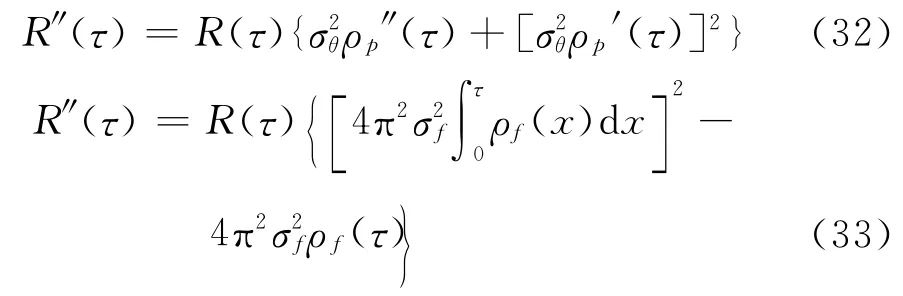
当赋予相关系数ρp（τ）和ρf（τ）具体的函数形式时，可以建立调制信号带宽BX与噪声信号方差的关系。

对于相位调制信号，当相关系数ρp（τ）分别为sinc函数、高斯函数和双边指数函数时：

对于频率调制信号，由式（33）得到R″（0）/R（0），因此，对于不同形式的相关系数，来决定。

4.实验仿真

为了验证结论的有效性，针对相关系数和方差对相关输出的影响进行了仿真实验。仿真的基本参数如表3所示，其中ΔR为目标距离与延迟线时延对应的距离之差，与ΔT的对应关系为ΔT＝2ΔR/c；ΔV为目标速度与延迟线提供的速度之差。在仿真结果图示中，横坐标轴的距离均对应于ΔR，纵坐标轴的速度均对应于ΔV.

表3 仿真参数

图3为直接发射随机噪声信号时噪声雷达系统的相关输出。图3（a）与图3（b）分别显示了发射信号的功率谱函数为矩形和高斯形时的相关输出。当噪声信号为矩形功率谱时，相关输出有明显的旁瓣产生，这是由sinc函数造成的，并使旁瓣具有一定的周期性。当功率谱函数为高斯形时，相关输出的主瓣相比矩形功率谱时较宽。对于能量一定的两种函数，高斯函数的能量主要集中在主瓣，而sinc函数的旁瓣分散了部分能量，从而造成了高斯形功率谱所输出的主瓣相对较宽。

图4所示为发射噪声相位调制信号，且相关系数ρp（τ）＝sinc（πBτ）时雷达系统的相关输出。图4（a）和图4（b）分别为σθ＝1和σθ＝1.5时的相关输出。对比图4（a）与图4（b），在大方差情况下，相关输出的旁瓣得到了有效抑制，主瓣变窄变尖锐，分辨率显著提高。

综合以上的推导，相位调制信号不适合采用类钟形功率谱函数，即相关系数为双边指数函数的情况。对于其他情况，结果可统一表示为＝，其中σ2为噪声源信号的方差，相位调制信号为，频率调制信号为；C为大于零的常数，不同情况下的取值不同。调制信号的带宽BX是方差σ2的单调增函数，因此BX随着方差σ2的增大而增大。

图5所示为发射噪声频率调制信号，且相关系数ρf（τ）＝exp（－｜τ｜/τ0）时相应的相关输出。图5（a）和图5（b）为σfτ0＝0.1和σfτ0＝0.15时对应的相关输出。双边指数形式的相关系数决定了其相关输出没有明显的旁瓣。因此，在方差较小时也没有旁瓣产生，但方差的增大使相关输出的主瓣能量更集中，使主峰变尖锐，分辨率得到提高。为了对仿真结果作定量分析，表4列出了不同方差下相关输出的主瓣宽度，同样反映出方差的增大能够使主瓣宽度变窄。

表4 不同方差下输出的主瓣宽度

实际中方差的选择要以主瓣宽度的要求为依据。以图4和图5的仿真为例，如果要保证相关输出的主瓣宽度小于1.5m，对于ρp（τ）＝sinc（πBτ）的相位调制信号，噪声源信号的方差应大于1；对于ρf（τ）＝exp（－｜τ｜/τ0）的频率调制信号，相应的方差选择应大于（0.2/τ0）2.

5.结 论

立足于分析随机噪声信号的数学特性，以相关系数和方差两项特征参数为基础深入分析了随机噪声雷达的相关输出特性。依据随机噪声雷达的基本工作原理得到了一般性的相关输出数学模型，在此基础上进一步建立了调制信号的相关输出数学模型，该模型依赖于噪声源信号的相关系数和方差。依据该模型分析了噪声源信号的相关系数和方差对相关输出和带宽的影响。

相关系数决定了相关输出的整体形式，当相关系数为sinc函数时，相关输出有明显的旁瓣；相关系数为高斯函数和双边指数函数时，均没有旁瓣产生，但相关系数为高斯函数时输出的主瓣较宽。方差直接影响相关输出的主瓣和旁瓣水平，方差的增大能够有效地抑制旁瓣，并使主瓣能量更集中，主峰变尖锐，分辨率得到显著提高。仿真结果有效地验证了结论，为波形的选择提供了依据。此外，通过取不同形式的相关系数得到了噪声源信号方差与调制信号带宽的关系，带宽可以表示为方差的单调增函数，因此方差的增大会导致带宽增大。

［1］刘国岁，顾 红，苏卫民.随机信号雷达［M］.北京：国防工业出版社，2005.

［2］LIU Guosui，GU Hong，SU Weiming.The development of random signal radars［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，35（3）：770－777.

［3］DMITRIY S，GARMATYUK，NARAYANAN R M.ECCM capabilities of ulrawideband bandlimited random noise imaging radar［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38（4）：1243－1255.

［4］高许岗，苏卫民，顾 红.随机噪声连续波SAR的性能分析［J］.电波科学学报，2010，25（1）：47－51.GAO Xugang，SU Weimin，GU Hong.Performance analysis of random noise CW SAR［J］.Chinese Journal of Radio Science，2010，25（1）：47－51.（in Chinese）

［5］张新相，吴铁平，陈天麒.随机噪声雷达抗干扰性能分析［J］.电波科学学报，2008，23（1）：189－194.ZHANG Xinxiang，WU Tieping，CHEN Tianqi.ECCM capabilities of random signal radar［J］.Chinese Journal of Radio Science，2008，23（1）：189－194.（in Chinese）

［6］NARAYANAN R M，XU Y，HOFFMEYER P D，et al.Design，performance and applications of a coherent ultra wide－band random noise radar［J］.Opt Eng，1998，37（6）：1855－1869.

［7］AXELSSON S R J.Noise radar using random phase and frequency moudlattion［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42（11）：2370－2384.

［8］AXELSSON S R J.Noise radar for range/Doppler processing and digital beamforming using low－bit ADC［J］.IEEE Transactions on Geoscience and Remote Sensing，2003，41（12）：2703－2720.

［9］FRY R D，GRAY D A.CLEAN deconvolution for sidelobe suppression in random noise radar［C］//2008 International Conference on Radar.Adelaide，SA，September 2－5，2008：209－212.

［10］程 娟，张冰尘，王岩飞.随机噪声雷达的脉冲压缩方法研究［J］.现代雷达，2008，30（2）：40－43.CHENG Juan，ZHANG Bingchen，WANG Yanfei.Study on pulse compression methods for random noise radar［J］.Modern Radar，2008，30（2）：40－43.（in Chinese）

［11］张先义.随机噪声超宽带成像雷达关键技术研究［D］.南京：南京理工大学，2008.ZHANG Xianyi.Research on key techniques of random noise ultra－wideband SAR［D］.Nanjing：Nanjing University of Science and Technology of China，2008.（in Chinese）

［12］WANG H，NARAYANAN R M，ZHENG Q Z.Through－wall imaging of moving targets using UWB random noise radar［J］.IEEE Antennas and Wireless Propagation Letters，2009，8：802－805.

［13］陆大金.随机过程及其应用［M］.北京：清华大学出版社，2007.