多仓库定位-运输路线安排问题的模型和算法研究

2012-08-07万凤娇

江汉大学学报（自然科学版） 2012年3期

关键词：仓库路线运输

万凤娇

（江汉大学商学院，湖北武汉 430056）

多仓库定位-运输路线安排问题的模型和算法研究

万凤娇

（江汉大学商学院，湖北武汉 430056）

针对现实问题的复杂性，考虑到单独研究物流设施选址和车辆运输路线安排问题的局限性，根据集成物流管理思想，综合考虑两个问题，重点研究了集成物流管理系统中多仓库定位-运输路线安排问题（LRP）。首先提出了LRP的数学模型，由于LRP属于NP-hard问题，提出了一种用于求解该类问题的两阶段混合启发式算法：禁忌搜索-蚁群混合算法。在选址阶段使用禁忌搜索算法求得一个较好的设施位置后，便转向运输路线安排阶段，并采用蚁群算法获得了一个与已得到的设施位置相对应的优化运输路线，这两阶段反复、连续运算，直到满足预先设置的终止条件。最后，给出算例验证模型和算法的有效性。

定位—运输路线安排问题；集成物流管理系统；禁忌搜索算法；蚁群混合算法

0 引言

近几年来出现了一种新的物流管理思想，即集成物流管理思想，此思想充分认识到设施定位、供应商和客户的分配以及运输路线安排问题之间的相互依赖关系，弥补了单独研究这些问题所带来的局限性，避免了配送方案的局部最优。物流定位-运输路线安排问题（Location-Routing Oroblem，LRP）一般表述为：给定了与实际问题相符的一系列客户点和一系列潜在的设施点，在这些潜在的节点中选择出一系列的设施位置，同时要确定出从各个设施到各个客户点的运输路线，确定的依据是满足问题的目标（通常是总的费用最小）。客户节点的位置和客户的需求量是已知的或可估算的，货物有一个或多个设施供应，每个客户只接收来自一个设施的货物，潜在设施点位置已知，问题的目标是把那些潜在的设施建立起来，以使总的费用最小。可见，LRP是物流选址-配给问题（Location-Allocation Problem，LAP）与车辆路线安排问题（Vehicle Routing Problem，VRP）的集成，但比后两者更复杂。目前关于LRP的研究比较多。Laporte等[1］研究了随机LRP模型，在随机LRP模型中仅仅当车辆到达客户处时才知道其需求量。Madsen[2-3］对求解定位-运输路线集成问题的方法进行了分析，后来又给出了有现实维度的两阶段定位-运输路线集成问题的方法。Daskin[4］考虑了随机时间的紧急服务的设施定位、车辆分配以及路线的选择问题。Chan等[5］建立了一个多仓库、多车辆、随机需求的定位-运输路线问题的数学模型，并给出求解的数学方法。Wu等[6］研究多仓库定位-运输路线问题，在所建立的模型中考虑了车辆派遣费用和不同车辆具有不同运载能力的约束，把LRP问题分解为物流选址-配给问题和车辆路线安排问题。国内对定位-运输路线安排问题的研究是在20世纪90年代后期才慢慢开始兴起，比国外滞后了30多年。目前对物流优化方面的研究还主要局限于对LAP和VRP的单独研究。汪寿阳、张潜、林岩等[7-9］是在国内较早开始研究LRP问题的学者，在其论文中对LRP问题的发展及其优化算法进行了综述。另外，张潜等[10］重点研究了集成化物流中一类特殊的定位-运输路线安排问题的两阶段启发式算法。

上述研究成果为集成物流管理系统的选址-选线问题的研究奠定了基础，但是多数研究成果仅考虑单级物流系统。本文则考虑多仓库的二级物流系统，对相关成本进行细化，以使相关模型得到进一步拓展，并给出了求解该问题的启发式算法。

1 模型的建立

目前对LRP的研究有很多种，传统的LRP模型所基于的物流网路是单级。本文研究的物流网络为典型的二级结构的网络，包括一个工厂、多个仓库和多个客户（见图1），研究的问题为多仓库LRP问题。

图1 典型的两级设施的LRP

1.1 模型的目标分析

1.1.1 总成本最低要合理安排集成物流系统中的各个环节以实现总成本最低。本文研究的LRP问题的总成本包括工厂的固定费用、仓库的建立和库存成本，以及车辆的指派成本和运输成本。

1.1.2 满足客户的要求在模型中我们考虑客户的需求是确定的，在供货期内合理地安排路径，尽可能地满足客户的需求。

1.1.3 准时到达近年来，出现了准时制（JIT）的概念，JIT不仅作为一种生产方式，也作为一种通用管理模式在物流、电子商务等领域得到推行。它要求货物要按照客户的需要准时到达，以提高物流服务质量，减少库存成本。

1.2 基本假设

在构建模型时，本研究对模型做了以下假设：①假设工厂的位置是固定的，仓库的位置是不确定的，需要从给定的潜在仓库中确定出合适的仓库；②有多个潜在的仓库，要求每个仓库供应多个客户的需求；③ 客户的需求为单一品种的商品，规格和价值相同；④每个客户仅能由一辆车和一个仓库为其提供服务；⑤ 运输车辆为同一类型，且每辆车在完成每次运输任务后返回到出发点；⑥每条巡回运输路线上的客户总需求不能超过车辆的载重能力；⑦ 假设车辆的行驶速度服从已知的连续分布；⑧ 假设客户需求是确定的；⑨ 考虑货物的相关成本包括货物本身的成本、订购成本和库存成本；⑩不考虑缺货成本。

1.3 模型参数及决策变量

集合：

S—系统中所有潜在仓库的节点集合，S=｛1，2，3，…，s｝；

H—系统中所有客户节点的集合，H=｛s+ 1，s+2，…，s+h｝；

K—系统中所有运输车辆的集合，K=｛1，2，…，k｝；

G—所有的仓库和客户的集合，G=S∪H。参数：

Fs—表示在s处建立或租用仓库的固定成本；Fp—表示工厂p的固定成本；

Cpi—表示工厂p到仓库i的单位运输费用，i∈S；

ypi—表示工厂p到仓库i的运量，i∈S；

C1—表示单位距离运输成本；

dij—表示节点i到节点j间距离，i，j∈G；

Ck—表示使用运输车辆k的固定成本，k∈K；

Qk—表示运输车辆k的容量，k∈K；

C2—表示货物的单位成本；

qj—表示客户j的需求量，j∈H；

Ri—表示仓库i的需求量，i∈S；

A—表示固定订购成本；

hi—表示仓库i的单位存储成本，i∈S；

Qi—表示仓库i的订货批量，i∈S。

模型中的决策变量：

xijk=1，如果运输车辆k经过节点i到节点j（i，j∈G，i≠j，k∈K）；否则，xijk=0；

Wpi=1，如果货物由工厂p运至节点i（i∈S）；否则，Wpi=0；

Zr=1，如果在节点r处建立或租用一个仓库（r∈S）；否则，Zr=0；

Yij=1，如果客户j被分配给仓库i（i∈S，j∈H）；否则，Yij=0。

1.4 数学模型

约束条件为：

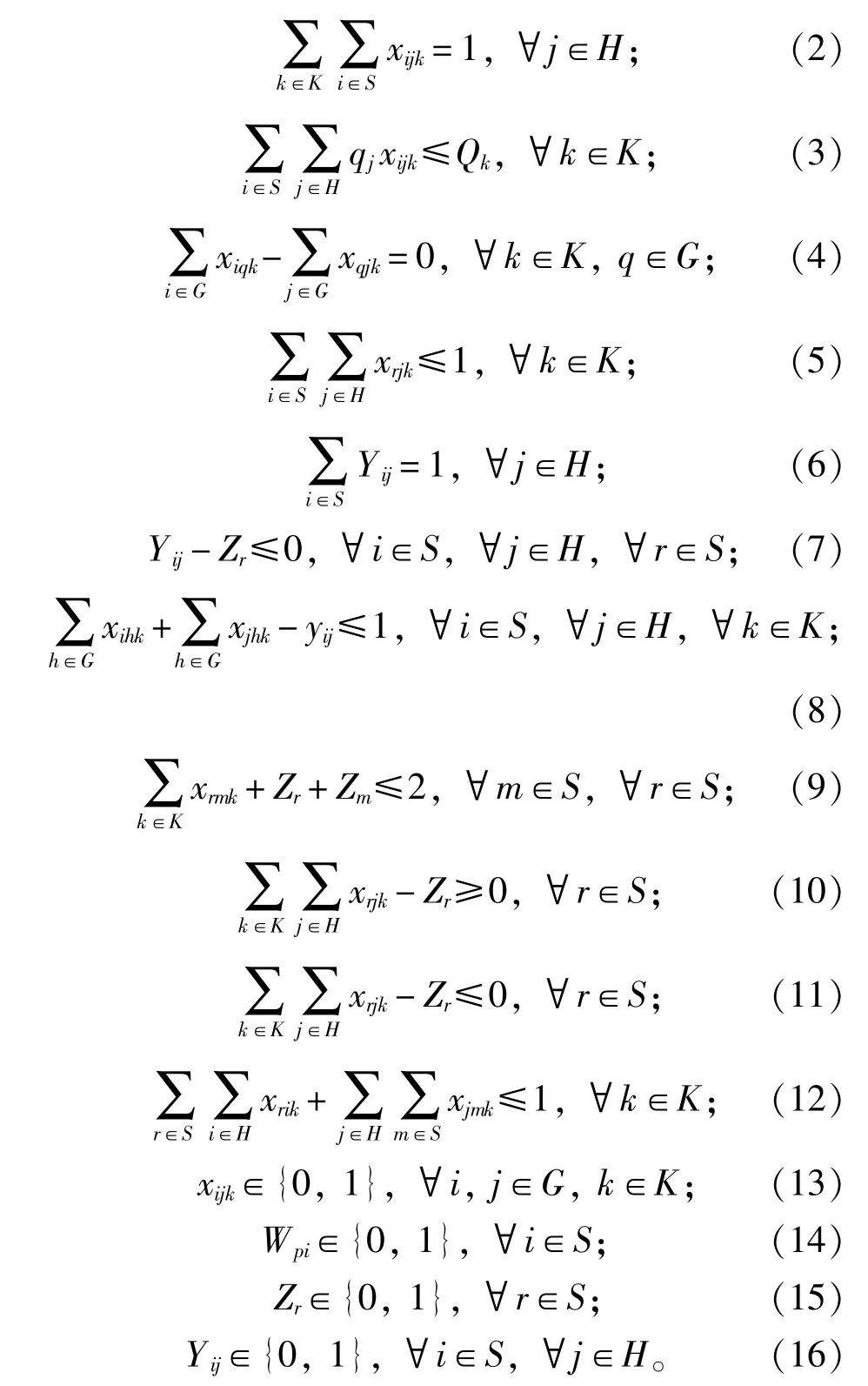
（1）式为目标函数，保证整个物流系统的总费用最小（包括设施固定费用、车辆运输费用和库存费用）；（2）式保证每一个客户仅由一辆车辆提供服务；（3）式为车辆容量约束，保证车辆承担的客户需求不超过车辆的容量；（4）式表示路线连续约束，即表示在一条路线上对每一个节点的货物来说由同一辆车运出；（5）式保证每辆车只为一个仓库服务；（6）式表示一个客户只能分配给一个仓库；（7）式表示只有当仓库开放时，才能给其分配客户；（8）式保证只有运输路线经过了客户节点，客户节点才可以被指派给仓库节点；（9）式保证在任意两个仓库之间无连接；（10）式和（11）式保证了每一运输车辆的行驶源于一个仓库且只能有一个起点；（12）式保证两个仓库不会在同一个行车路线上；（13）～（16）式保证决策变量为整数。

2 算法设计

在启发式算法中，禁忌搜索算法具有全局寻优能力，而且比较容易实现，但其局部搜索性能易受分散性的影响。蚁群算法引入正反馈并行机制，具有较强的鲁棒性、优良的分布式计算机制，易于与其他方法结合的优点，但其全局优化性能的优劣在很大程度上与蒸发系数的选择有关，如选择得不合适易使算法陷于局部最优。因此，本文将两种方法组合在一起，可以弥补各自的不足，充分发挥其长处。根据所建立的LRP数学模型的特点，采用禁忌搜索-蚁群混合算法对问题进行求解。

为了有效求解多仓库LRP，根据问题的不同决策变量，将其分解为LAP和VRP两个子问题分别求解。由于仅仅有一些路段会随着仓库位置的改变而发生变化，因此，可以将搜索限制在这些路段内。所以，车辆路线安排阶段实际上是局部搜索，而不是移动所有线路的全局搜索，这就会消除很多不必要的计算，并允许两阶段算法在合理的计算时间内求得较优解。

2.1 初始化

由于禁忌搜索算法都是以初始解开始的，所以在进行计算之前需要先计算初始解。由于禁忌搜索算法对初始解的依赖性较强，一个较好的初始解可使禁忌搜索在解空间中搜索到更好的解，而一个较差的初始解则会降低搜索的收敛速度和搜索质量。为此，我们使用贪婪取走启发式算法（Greedy—Drop Heuristic Algorithm）获得一个较好的初始解，来提高算法的性能。Greedy—Drop的基本思想是从所有候选选址点中，逐个将对目标函数影响最小的选址点去掉直到剩余的选址点只剩下m个。

2.2 定位——分配阶段（LAP)

初始解确定了所选的仓库节点以及每个仓库节点所服务的客户，采用禁忌搜索算法改进初始解，得到一个当前较好解。设定N为网络中所有n个潜在候选仓库节点的集合，S为所选点集，N（S）=｛S1，S2，…，Sp（n-p）｝为与之相对应的领域，p为给定的选址数量。最后我们令tabu_tag（i）表示节点i所处的禁忌状态，如tabu_tag（i）=t表示节点i在接下去的t步内将处于禁忌状态。

第一阶段：采用贪婪取走启发式算法（Greedy—Drop Heuristic Algorithm）获得初始解。

第二阶段：采用禁忌搜索改进算法。

Step 1：输入算法的运行参数，包括终止迭代步数T，每次迭代搜索当前解的邻居的个数M，禁忌长度l，对不可行方案的惩罚函数Pw等；初始化迭代步数、禁忌状态和禁忌表，令t= 0，tabu_tag（i）=0，H=φ；确定当前最好解S0，令S0=S，利用解的评价方法计算S的评价值E。

Step 2：对当前最好解S用两两交换法（2-Swap）实施领域操作，如果两交换的点不是禁忌表H中的元素，则得到S的一个领域S*，利用解的评价方法计算解S*的评价值E*，然后采用蚁群算法求解路径安排问题，更新禁忌表。

Step 3：判断是否满足终止迭代步数T。如果满足，输出结果，算法停止。否则，继续Step 2。

2.3 车辆路线安排阶段（VRP)

基于定位-分配阶段求解的设施定位及客户分配，在算法的第二阶段使用蚁群算法求解VRP，通过迭代循环实现算法中两阶段搜索的协调，直到满足预先设置的终止条件。根据蚁群算法的基本原理，求解VRP的蚁群算法的基本步骤如下：

Step 1：初始化参数。设循环次数Nc=0，最大循环次数Nmax为一常数，令路径（i，j）的初始信息量τij（t）=const（const为常数），禁忌表tabuk=φ；

Step 2：采用最近邻域法获得初始解；

Step 3：将m只蚂蚁随机放在n个仓库中，并为其分别建立禁忌表；

Step 4：循环次数Nc=Nc+1；

Step 5：令蚂蚁禁忌表索引号k=1；

Step 6：k=k+1；

Step 7：对于m只蚂蚁，在候选节点集中，根据状态转移概率公式选择下一个客户节点j，j∈｛allowk-tabuk｝；

Step 8：计算线路上的载重量q，若q＜Q（Q为车辆的额定载重量），则转至下一步，否则将节点j重新放回到可选客户点集allowk中；

Step 9：判断可选客户集allowk，若allowk=φ，则转至下一步；若没有访问完可选客户集合allowk中的所有点，即k＜m，则从allowk中选择未被搜索的点，跳转至Step 6，搜索下一个节点；

Step 10：当m只蚂蚁选择到下一个节点后，对其所走过的路径，根据公式τijnew=（1-ρ）τijold+ ρτ0（τ0为路径上信息量的初始值）进行信息素的局部更新和信息素增量τij的更新；

Step 11：计算每只蚂蚁搜索的最短路径的长度，若k=m，则进行信息素的全局更新；

Step 12：判断循环次数Nc是否大于最大循环次数Nmax；若满足约束条件，则循环结束，输出计算结果；否则，清空禁忌表，并跳转至Step 3。

物流定位-运输路线安排问题的算法流程图如图2所示。

图2 物流定位-运输路线安排问题算法流程图

3 算例分析

设计一个基本算例。假设某二级结构物流网络中，有1个工厂，6个潜在仓库，30个客户需求点，工厂P的坐标位置为（42，195），工厂P的固定费用为9 500元，工厂P到仓库Di（i=1，2，…，6）之间的单位运输费用如表1所示，潜在仓库和客户需求点的位置坐标（x，y）在200×200的范围内随机分布（见图3）。潜在仓库的坐标位置及其固定费用如表2所示，客户的需求量如表3所示。潜在仓库之间以及与客户需求点之间的距离见表4所示。潜在仓库到各客户需求点以及各客户需求点之间的单位距离运输费用为1元，车辆的额定载重量为2.5 t，车辆平均行驶速度为70 km/h，使用车辆的固定成本为600元，货物的单位成本为0.25元，固定订购成本为20元，hi为24%。

表1 工厂到仓库之间的单位运输费用 /（元·kg-1）

潜在仓库和客户需求节点之间的距离可以通过下面公式计算：

在此，我们采用两阶段禁忌搜索—蚁群混合算法对该算例进行求解，参数设置如下：

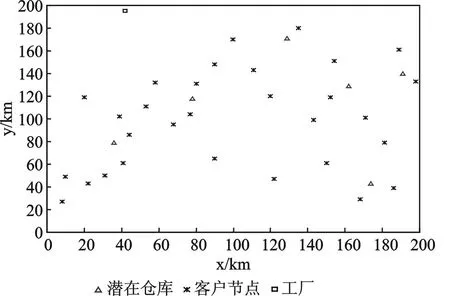
图3 潜在仓库和客户的位置分布图

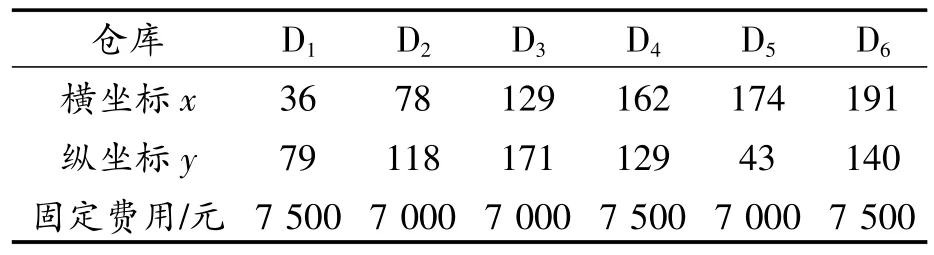
表2 潜在仓库的坐标位置及其固定费用

①禁忌搜索的交换操作的最大次数为9；②禁忌表长度为9；③禁忌搜索的最大迭代次数为50次；④蚂蚁的个数与客户的个数相同；⑤信息素重要程度的参数α=1.0；⑥启发式因子重要程度的参数β=1.0；⑦信息素蒸发系数ρ=0.9；⑧信息素增加强度系数Q=0.5；⑨蚁群算法的迭代次数为50次。

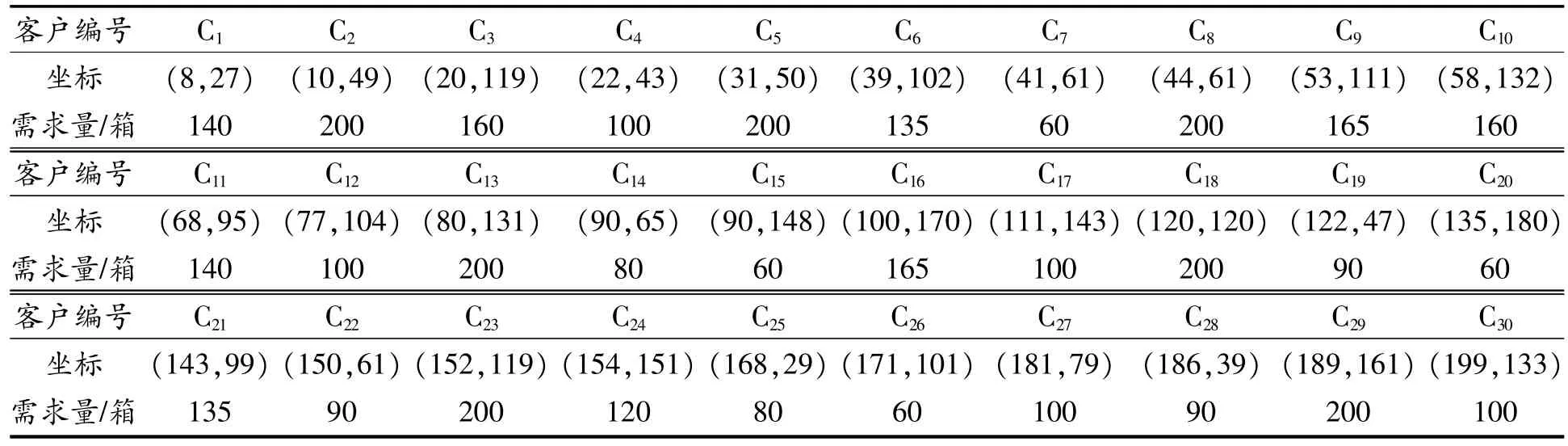
表3 客户需求点的坐标位置、需求量

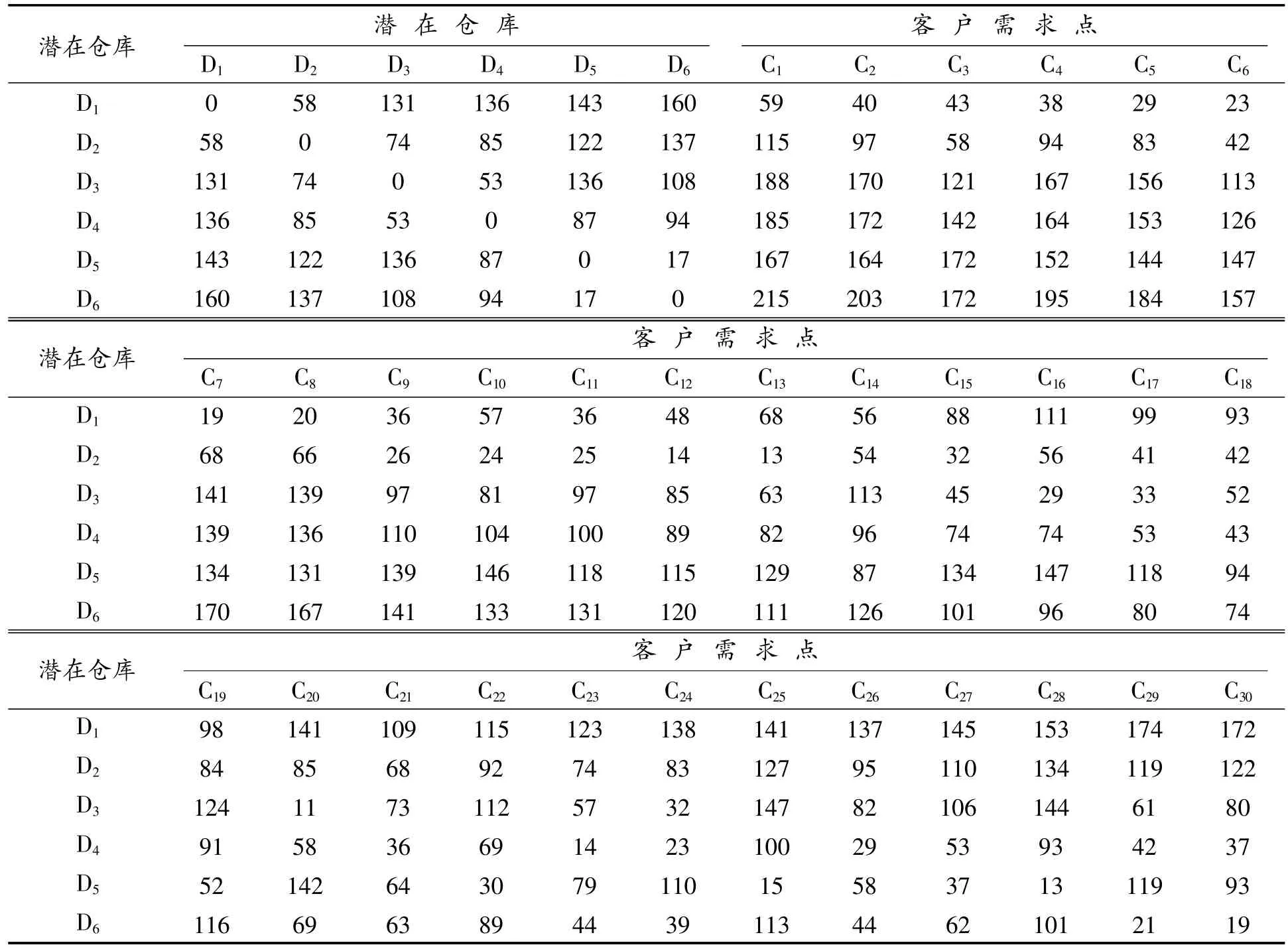
表4 潜在仓库之间以及与客户需求点之间的距离/km

仿真计算，使用MATLAB7.0编程实现。经过计算后，得到目标函数的最优解为43 088.77元。其选址与选线安排如图4，算法的平均解随迭代次数变化的趋势如图5，算法的最优解随迭代次数的变化趋势如图6。

图4 选址选线运行路线图

图5 平均解随迭代次数的变化趋势

图6 最优解随迭代次数的变化趋势

经过计算，选定的仓库和仓库所服务的客户见表5，最优运输路线见表6。

表5 设施选址阶段（LAP)的解

表6 运输路线优化阶段（VRP)的解

4 结语

本文给出多仓库定位-运输路线安排问题的数学模型，并提出了采用两阶段禁忌搜索-蚁群混合算法求解该LRP问题。将LRP问题分解成两个子问题分别求解，即选址定位问题和路线安排问题，在定位阶段使用禁忌搜索算法得到一个好的设施选址结构后，便转向运输路线安排阶段，并使用蚁群算法获得了一个与已得到的选址结构相对应的优化运输路线，这两阶段反复、连续运算，直到满足预先设置的终止条件。此禁忌搜索-蚁群混合算法可以在一定程度上克服单一启发式算法在局部搜索能力方面的不足，从而能得到比其他启发式算法更好地计算结果。最后，通过算例分析进一步验证了该算法的有效性和可行性。因此，本文提出的两阶段混合启发式算法为解决集成物流管理系统中的LRP问题求解提供了新的方法。后续进一步的研究将考虑缺货成本对于系统总成本的影响。

[1］Laporte G，Louveaux F，Mercure H.Models and exact solutions for a class of stochastic location-routing problems[J］.European Journal of Operational Research，1989，39：71-78.

[2］Madsen O B G.A survey of methods for solving combined location-routing methods[M］//Jaiswal N K.Scientific Management of Transport Systems.North-Holland：Amsterdam，1981：194-201.

[3］Madsen O B G.Methods for solving combined two level location-routing problems of realistic dimensions[J］. European Journal of Operational Research，1983，12：295-301.

[4］Daskin M S.Location，dispatching，and routing models for emergency services with stochastic travel times [M］//Ghosh A，Rushton G.Spatial analysis and location-allocation models.New York：Von Nostrand Reinhold Company，1987：224-265.

[5］Chan Y，Carter W B，Burnes M D.A multiple-depot，multiple-vehicle，location-routing problem with stochastically processed demands[J］.Computers& Operations Research，2001，28：803-826.

[6］Wu T H，Low C Y，Bai J W.Heuristic solutions to multi-depot location-routing problems[J］.Computers &Operations Research，2002，29：1393-1415.

[7］汪寿阳，赵秋红，夏国平.集成物流管理系统中的定位-运输路线安排问题的研究 [J］.管理科学学报，2000，3（2）：69-74.

[8］张潜，高立群，胡祥培.集成化物流中的定位-运输路线安排问题（LRP）优化算法评述[J］.东北大学学报，2003，24（1）：31-34.

[9］林岩，胡祥培，王旭茵.物流系统优化中的定位-运输路线安排问题（LRP）研究综述[J］.管理工程学报，2004，18（4）：45-49.

[10］张潜，高立群，刘雪梅，等.定位-运输路线安排问题的两阶段启发式算法[J］.控制与决策，2004，19（7）：773-777.

WAN Feng-jiao
（School of Business，Jianghan University，Wuhan 430056，Hubei，China）

Considering the complication of the realistic problem and the limitation of research into locations-routing problem of logistics separately and integrated logistics，the paper studies location-routing problem including multi-depot in integrated logistics.Model of LRP is given on the basis of some hypotheses.Because LRP is NP-hard problem，a two-phase heuristic approach for solving the LRP is proposed.In location-allocation phase，after the candidate facilities and their customers are determined by using taboo-search algorithm，vehicle routing phase is assorted to by adopting ant colony algorithm to search the optimal routes.These two phases operate repeatedly and continuously until meeting the condition of termination.At last，the dissertation gives an example to illustrate the model and algorithm effectiveness.

location-routing problem；integrated logistics；taboo-search algorithm；ant colony algorithm