一类临界指数增长的椭圆型方程组正解的存在性

2012-08-07万优艳

江汉大学学报（自然科学版） 2012年3期

关键词：椭圆型位势有界

万优艳

（江汉大学数学与计算机科学学院，湖北武汉 430056）

一类临界指数增长的椭圆型方程组正解的存在性

万优艳

（江汉大学数学与计算机科学学院，湖北武汉 430056）

研究了一类临界指数增长的椭圆型方程组。通过变分法，得到方程组的能量泛函在零点附近的局部极小值点的存在性，且该极小值点为方程组的正解。证明了当方程组的扰动项趋于零时，方程组的正解也趋于零。

临界指数；椭圆型方程组；正解

0 引言

考虑下列临界指数增长的椭圆型方程组：

其中Ω是RN（N=3）中光滑有界区域，α＞2，β＞且f（x），g（x）满足：（A1）f（x），g（x）∈H-1（Ω），且f（x）≥0，g（x）≥0。

由文献[1］可知，当Ω是RN中的有界星形区域时，带临界指数增长的椭圆型方程

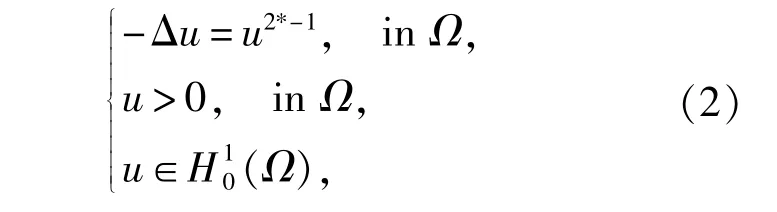
是无解的。但当方程（2）中出现位势和扰动项且当位势和扰动项满足一定条件时，方程（2）存在解[2］。Adachi和Tanaka[3］证明了RN中次临界方程当出现扰动项且扰动项满足一定条件时正解的存在性。Benci和Cerami[4］研究得到RN中临界方程出现位势且位势满足一定条件时正解的存在性。

对于方程组（1），Alves等[5］研究得到：当Ω是RN中的有界星形区域且方程组（1）的位势与扰动项f（x）和g（x）都为零时，方程组（1）无解。

受单个方程（2）研究结果的启发，本文讨论当位势为常数1且扰动项满足条件（A1）时，方程组（1）正解的存在性。

1 预备知识

记E为Sobolev空间该空间的范数定义为

记＜·，·＞E为该空间的内积。记E*为E的对偶空间H-1（Ω）×H-1（Ω）。令

根据文献[5］中的定理5，有

定义泛函I（u，v）：E→R，

引理1 假设（f（x），g（x））∈E*，那么

（i）I（u，v）∈C2（E，R），并且任给（φ，φ）∈E，有

（ii）如果f（x）和g（x）都是非负函数，（u，v）∈E是I（u，v）的一个临界点，那么（u，v）是方程组（1）的一个非负解。此外，如果u（x）≢0，v（x）≢0或者f（x）≢0，g（x）≢0，那么（u，v）是方程组（1）的一个正解。

证明（i）证明方法见文献[1］中性质1.12。

（ii）假设（u，v）∈E满足I′（u，v）=0。由（4）式知，任给（φ，φ）∈E，有

于是u-=0 a.e.Ω且v-=0 a.e.Ω，即u≥0，v≥0。如果u（x）≢0，v（x）≢0或者f（x）≢0，g（x）≢0，由强极值原理可得u和v在Ω中是正的。

引理2 假设（f（x），g（x））∈E*，那么存在r1＞0和d1＞0，使得

（i）I（u，v）在r1｝是严格凸的；

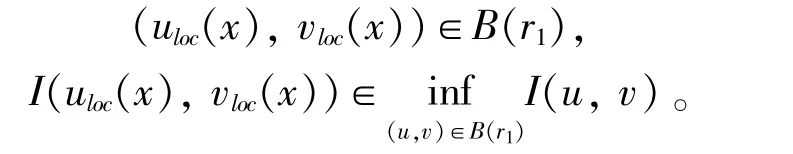
证明（i）由（5）式和Sα，β，Sα+β的定义可知，任给（φ，φ）∈E，有

因此，I″（u，v）在（u，v）∈B（r1）中是正定的，I（u，v）在B（r1）中是严格凸的。

证明因（uloc（x），vloc（x））是I（u，v）的临界点，所以任给（φ，φ）∈E，都有

即

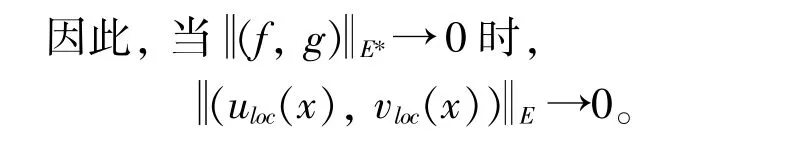
2 主要结果

证明由引理1、引理2和引理3可得证。

[1］Willem M.Minimax theorems[M］.Basel：Birkhäuser，1996.

[2］Wan Y，Yang J.Multiple solutions for inhomogeneous critical semilinear elliptic problems[J］.Nonlinear Analysis，2008，68：2569-2593.

[3］Adachi S，Tanaka K.Four positive solutions for the semilinear elliptic equation：-Δu+u=a（x）up+f（x）inRN[J］.Calculus of Variations and Partial Differential Equations，2000，11：63-95.

[4］Benci V，Cerami G.Existence of positive solutions of the equationJ of Funct Anal，1990，88：90-117.

[5］Alves C O，de Morais Filho D C，Souto M A S.On systems of elliptic equations invbolving subcritical or critical sobolev exponents[J］.Nonlinear Analysis，2000，42：771-787.

WAN You-yan
（School of Mathematics and Computer Sciences，Jianghan University，Wuhan 430056，Hubei，China）

This paper studies an elliptic system involving Sobolev critical exponent.By the variational methods，we can obtain the existence of local minimum point of the energy functional related to the system which is near zero，and the local minimum point is the positive solution to this system.Moreover，It is also proved that this positive solution tends to zero when the perturbed term goes to zero.

critical exponent；elliptic system；positive solution