航空制孔机器人末端垂直度智能调节方法
2012-08-07公茂震袁培江王田苗
公茂震 袁培江 王田苗 张 睿
(北京航空航天大学 机械工程及自动化学院,北京100191)
据统计,大多数飞机机体疲劳失效事故源于结构连接部位的疲劳裂纹,而疲劳裂纹大多产生在连接孔处[1],因此连接处孔的加工质量极大影响着飞机的安全性和使用寿命.孔的垂直度是影响孔的加工质量的主要因素之一,它不仅会使孔的直径发生改变[2],而且在飞机的装配过程中会影响铆接质量从而导致机构连接的不稳定[3-4].在机器人自动钻孔过程中,孔的垂直度取决于钻头的中心轴线和钻孔点处法线的重合程度,所以钻头的垂直度调节对保证钻孔的加工质量起着至关重要的作用.
钻头的垂直度调节主要由2部分组成:曲面的法线测量和钻头的姿态调整.目前,设备很难靠自身控制使钻头沿钻孔点的法线方向钻孔[5],需要利用法线测量与末端调姿装置来调整钻头的姿态.对于曲面的法线测量,近些年来国内外已有大量的研究.向量叉积法[6]虽然计算简单,但是精度低;二次曲面拟合法[7]对二次曲面精度很高,但对一般的曲面具有一定的局限性;NURBS曲线法[8]和三角网格法[9]都要测量大量的点才能达到较高的精度,不适合实时的精确测量.本文针对以上出现的问题提出了一种基于3个激光测距传感器的非接触法线测量方法,此方法测量精度高,速度快,且不会损伤被测物体表面.对于钻头的姿态调整,大多数研究工作从调整被加工工件来相对的调节钻头的姿态,比如三点快速调平算法[10]和最近发明的一种带角度自动调节装置的钻孔设备[11].但对于像飞机蒙皮这样大型的不易移动的工件,这些方法就难以实现其垂直度的调节.本文从调节钻头实体的角度出发提出了一种二元角度调节方法,它可以精确容易的实现钻头定角度的姿态调整.
最后,在自行研制的航空制孔机器人平台上进行实验,实验证明了法线测量的高精度和高效性及钻头姿态调整的准确性和有效性.
1 垂直度调节方法设计
航空制孔机器人系统的钻孔过程由4部分组成:视觉定位、法线测量、钻头姿态调整和判断钻孔.其中法线测量和钻头姿态调整称为钻头的垂直度调节,是机器人制孔的关键技术和难点.
在钻孔前首先需要视觉系统识别并定位被标记的钻孔点P.然后机器人的末端执行器移动至P处,利用3个激光测距传感器测量并计算P处的单位法向量eN.再判断eN和钻头的轴线к的夹角φ是否在偏差范围内:若φ在偏差范围内则锁定钻头直接进行钻孔;若φ不在偏差范围内则利用二元角度调节方法对钻头的姿态进行调整,使钻头最大程度的沿P点的法线方向钻孔,保证钻孔的加工质量.
假设偏差范围为±0.5°,激光测距传感器测量的3个特征点为Vi(i=1,2,3),钻孔过程的详细流程图如图1所示.
2 曲面法线测量
2.1 系统建模与坐标计算
本文中的3个激光测距传感器的发射点Mi(i=1,2,3)均匀的分布在钻头同心的圆周E上,并且此3个发射点在同一个平面π1上,如图2所示.钻头所在的中心轴线к与平面π1垂直,且与平面π1的交点为点O.以点O为原点建立笛卡儿坐标系 Oxyz,其中 x轴通过点 M1,y轴平行于M2M3,z轴沿钻头的中心轴线к方向.
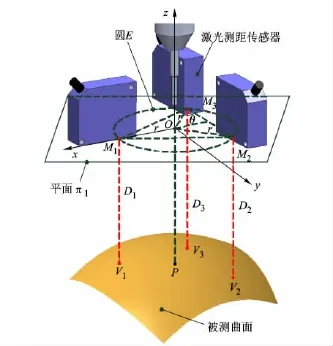
图2 曲面法线测量示意图
在测量过程中3个激光测距传感器可测得点Mi(i=1,2,3)与相对应的3 个特征点 Vi(i=1,2,3)之间的距离 Di(i=1,2,3),所以点 Vi(i=1,2,3)的z坐标可以表示为

若圆E的半径为R,根据等边三角形的几何性质可得3个特征点Vi(i=1,2,3)的x和y坐标:

由于△M1M2M3是等边三角形,所以式(2)中的θ=30°,根据式(1)和式(2)可得特征点Vi(i=1,2,3)的坐标为
2.2 法向量计算
在坐标系Oxyz中,假设P点的坐标为(xP,yP,zP).由于点 Vi(i=1,2,3)和 P 是曲面上的 4个点,所以此4点不共面,因此P点和Vi(i=1,2,3)中任意2点都能确定1个平面,以点P,V1,V2为例,此3点确定唯一的平面π2,如图3所示.

图3 法向量的计算示意图
平面π2与曲面的交线是一条曲线V1PV2,以同样的方法可以得到另外2条交线:曲线V2PV3和曲线V3PV1.显然,曲线V1PV2在平面π2上,因此由P,V1,V23点可求出平面π2的一般式方程:

平面π2和被测曲面的交线近似为一椭圆,因此在平面π2上可以找一个合适的点Q(xQ,yQ,zQ)作为一个椭球体的中心,P,V1,V23点可以确定唯一的椭球体.椭球体的解析式可表示为


然后用平面π2和椭球的交线Σ来近似的代替交线Q1PQ2.交线Σ可由式(3)和式(4)表示为

对式(5)利用雅可比行列式可求得曲线Σ在点P处的切线为
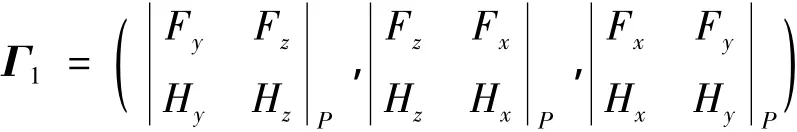
同理,可求得曲线V2PV3和V3PV1的近似切向量Γ2和Γ3,过曲面上一点且在曲面上的任意曲线在该点处的切向量都与曲面在此点处的法向量垂直[12],因此由叉积可得P处的3个法向量:
由于曲面上的3个点确定的平面π2与曲面的交线是用逼近的解析式来近似代替的,所以求得的法向量也存在一定的误差.要使计算出的法向量更准确就需要求此3个向量的平均值,而加权求法向量的平均值更接近理论值[13].本文采用角度加权平均法[14]可得加权平均后点P处曲面法向量N的单位法向量:

式(6)中的 i=1,2,3,wi是权因子,角度加权平均法的权因子如式(7)所示:
3 钻头姿态调整
图4所示为定角度二元调整装置,其上下为2个固定台,中间为2个相同的楔形旋转台.调整时,2个旋转台旋转可以使钻孔末端执行器的钻头围绕固定中心线实现三维空间运动,即实现一个圆锥运动.若2个旋转台向适当的方向旋转适当的角度,便可以实现定角度的调节.定角度二元调整方法可大幅度的降低系统复杂程度,减小系统重量和体积.
二元角度调整机构可带动钻削机构作约4°的角度偏转.如图5a和图5b所示,2个楔形旋转台的倾角为α,当它们处于图5a状态时,旋转台1固定,旋转台2沿顺时针方向绕斜面的中心轴线转动,此时钻头也沿顺时针做圆锥摆动,当旋转台2达到极限位置时钻头达到最大的摆动角度φmax,根据几何性质可得到α与φmax的关系:

图4 二元角度调节

再同时转动旋转台1和2使其到图5b所示状态,同样旋转台1固定,旋转台2沿顺时针方向绕斜面的中心轴线转动,此时钻头将会在初始位置的另一侧沿顺时针做圆锥摆动.这样只要适当的转动2个旋转台便可以实现钻头达到其周围4°以内的任何区域,从而实现法向角度调整.由于此机构利用步进电机通过齿轮传动使装置转动,因此可以对钻头进行实时精确地定角度调整.

图5 钻头的二元角度调节过程
要使钻头调整到与第2节计算出的法向量重合,需要求出钻头与法向量的夹角φ和法向量绕z轴在xOy平面上转过的角度β.假设曲面在钻孔点P处的单位法向量为 eN=(xe,ye,ze),而钻头的方向向量为ez,于是可以得到

如图5c所示,MO为钻头的初始位置,MR为钻头调整后所在的位置,VMO与VMR之间的夹角即为钻头与法向量的夹角φ.角度γ是钻头由MO处调整到MR处时旋转台2旋转的角度,假设|VMO|=L,在ΔMOMRMmax中根据几何性质可得
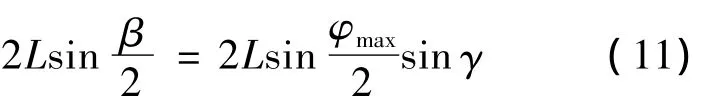
将式(9)代入式(11)中解得

钻头的调节过程为旋转台1和2同时从初始位置顺时针绕中心轴旋转(β-γ),旋转台1固定,旋转台2顺时针转动γ即可完成钻头姿态的调整.
4 实验
本实验以自行研制的航空制孔机器人为实验平台,如图6a所示.激光测距传感器采用德国SICK公司的小型测距传感器,其测量精度为±100 μm,测量范围为65 mm ~105 mm.

图6 航空制孔机器人系统
航空制孔机器人系统的控制系统采用奥地利B&R公司的实时控制系统,如图6d所示.在Automation Studio(AS)编程环境下进行编程,其数据处理精度为±5 μm,实时的刷新时间为10 ms.
3个激光测距传感器均匀的分布在钻头的周围,如图6b所示,其3个激光发射点等边的位于同一个圆上,此圆的实际半径为R=57.5 mm.di(i=1,2,3)表示激光测距传感器测得激光发射点与3个特征点的距离,故可得3个特征点的坐标.在飞机蒙皮上选择3个不同的点进行法线的测量,实验数据如表1所示.在二元角度调节装置部分,如图6c所示,2个旋转台由2个步进电机通过齿轮传动带动其旋转,步进电机的步距角为0.18(°)/步,齿轮的传动比为 1∶3,因此控制系统每发一个脉冲旋转台旋转0.06°,其最终调节精度可达0.08°.在钻头调整时,3个激光测距传感器测得3个距离,经控制器AI模块和控制器X20,由以太网通信将数据传输到AS中.数据在AS中进行处理,计算出P点的单位法向量eN和eN与钻头的夹角φ和角度β,再将其换算为2个电机需要的脉冲数控制2个旋转台进行精确的旋转,达到调整钻头垂直度的目的.
图7所示为钻头垂直度调整前后系统钻孔的质量,并对调整后的孔利用内径千分尺从0°开始每隔30°测一次直径,计算孔的圆度.通过对比和对孔圆度的分析发现孔的质量明显得到提高,这证明了此算法的可行性和精确性.

表1 法向量测量数据

图7 钻头垂直度调整前后钻孔对比
5 结论
1)基于3个激光测距传感器的曲面法线测量方法建模简单,测量过程中3个激光测距传感器同时测距,数据的反馈和处理时间短,提高了钻孔的效率;法向量计算算法精确度高,保证了航空制孔的质量.
2)二自由度角度调节法用一套运动机构实现两轴运动,不仅减小了运动机构的体积,而且可以使钻孔部件按照设定角度整体偏转;它将阶梯状传统两轴插补运行轨迹转变为纯粹的二点连线的极坐标定位,从而路径最短且平滑,提高了调整的速度和精确度.
References)
[1]Bakuckas J G,Bigelow C A,Tan P W.Characterization of fatigue behaviour of aircraft fuselage structure[C]//Proceedings of the 22nd Symposium of the International Committee on Aeronautical Fatigue.Lucern,Switzerland:EMAS,2003:5 -9
[2]Wang Min,Xue Shaoding,Jiang Hongyu,et al.Development of knowledge-based system on aircraft assembly drilling process[C]//IEEE International Conference on Information Science and Engineering(ICISE).Hangzhou:IEEE,2010:1 -4
[3]Proppe C.Probabilistic analysis of multi-site damage in aircraft fuselages[J].Computational Mechanics,2003,30(4):323 -329
[4]Lutters W G,Ackerman M S.Achieving safety:a field study of boundary objects in aircraft technical support[C]//Proceedings of ACM conference on Computer Supported Cooperative Work.New York:ACM,2002:266-275
[5]Devlieg R,Szallay T.Applied accurate robotic drilling for aircraft fuselage[J].SAE International Journal of Aerospace,2010,3(1):180-186
[6]Hasegawa N,Okada T,Shimizu T.Measurement of surface-normal using a range sensor with a pair of wedge-prisms[C]//IEEE International Conference on Instrumentation and Measurement Technology(IMTC).Ottawa,Canada:IEEE,2005,1744 -1749
[7]应高明,王仲奇,康永刚,等.飞机壁板自动钻铆法向量测量方法研究[J].机床与液压,2010,38(20):1 -4 Ying Gaoming,Wang Zhongqi,Kang Yonggang,et al.Study on normal vector measurement method in auto-drilling and riveting of aircraft panel[J].Machine Tool & Hydraulics,2010,38(20):1-4(in Chinese)
[8]蔺小军,王增强,单晨伟.自由曲面CMM测量测头半径补偿方法[J].航空制造技术,2011(10):75 -77,85 Lin Xiaojun,Wang Zengqiang,Shan Chenwei.Method of probe radius compensation for free surface measurement[J].Aeronautical Manufacturing Technology,2011(10):75 - 77,85(in Chinese)
[9]Page D L,Sun Y,Koschan A F,et al..Normal vector voting:crease detection and curvature estimation on large,noisy meshes[J].Graphical Models,2002,64:199 -229
[10]秦现生,汪文旦,楼阿莉,等.大型壁板数控钻铆的三点快速调平算法[J].航空学报,2007,28(6):1455 -1460 Qin Xiansheng,Wang Wendan,Lou Ali,et al.Three-point bracket regulation algorithm for drilling and riveting of aerofoil[J].Acta Aeronautica et Astronautica Sinica,2007,28(6):1455-1460(in Chinese)
[11]夏长洪.一种带角度自动调节装置的钻孔设备:中国,201833210U[P].2011-5-18 Xia Changhong.A drilling equipment with automatic angle adjustment:China,201833210U[P].2011-5-18(in Chinese)
[12]Gerald F.Curves and surface for CAGD:a practical guide[M].San Francisco:Morgan Kaufmann,2002:261 -263
[13]Jin Shuangshuang,Lewis R,West D.A comparison of algorithms for vertex normal computation[J].The Visual Computer,2005,21(1/2):71-82
[14]Klasing K,Althoff D,Wollherr D,et al.Comparison of surface normal estimation methods for range sensing applications[C]//IEEE International Conference on Robotics and Automation(ICRA).Kobe:IEEE,2009:3206 -3211
