基于虚网格的格心ADT搜索法

袁 武 阎 超 于 剑 杜若凡

(北京航空航天大学国家计算流体力学实验室，北京100191)

寻点方法是重叠网格［1－6］的关键技术之一，“寻点”是确定网格点在其他网格中的位置、查找网格贡献单元的统称.由于在重叠网格的生成过程中需要大量地进行“寻点”操作，因而准确与效率是寻点方法的关键.

常见的寻点方法有遍历法、Stencil Walk［7］、反变换(Inverse Map)［8］、ADT(Alternating Digital Tree)搜索［9－10］等.其中，ADT 搜索方法用笛卡儿坐标下的包围盒(min，max)对物体进行特征描述，由包围盒是否相交来判断物体的相交关系.由于包围盒相交关系的判断非常简单，因此，ADT方法效率很高，且特别适合对几何不规则目标进行搜索.

本文提出了一种直接在格心网格下操作、基于虚网格概念的ADT搜索方法，能有效提高寻点方法的效率和可靠性，并通过数值算例对新方法进行了验证.

1 本文方法

1.1 格心ADT搜索

目前，基于格心网格的有限体积法在CFD(Computational Fluid Dynamics)中应用广泛.在格心网格的寻点问题中，由于网格分区的关系，在分区边界上，格心网格单元跨越多个子区，单元顶点位于不同子区内，难以给出格心网格单元的唯一位置标识，格心网格单元在逻辑空间上不封闭，这给ADT树的建立带来不便.一种解决办法［11］是，仍然借用格点网格生成ADT树，然后找到P点的格点贡献单元，以该格点网格为顶点的格心网格必然比较靠近P点，再结合Stencil Walk方法，在附近找到真正的格心贡献单元，但Stencil Walk方法存在局部收敛性要求，若初始位置单元不合理，Stencil walk方法有可能收敛不到合理贡献单元而导致寻点失败.

另一种思想就是直接在格心网格下进行ADT搜索，搜索结果是可能的格心贡献单元集合，再利用点面位置关系对结果列表进行逐一判断，即得到合理贡献单元.不同于格点网格下搜索结果是解的附近某位置，格心网格下搜索结果是一个包含解的集合，故可以完全摒弃不稳定的Stencil Walk方法，直接对搜索结果列表进行遍历，有效提高了寻点方法的可靠性.

格心网格下建立ADT树的关键是使搜索空间完整封闭，问题描述如图1所示，本文图例均以实线表示格点网格线，虚线表示格心网格线.在分区边界上，格心单元跨越多个子区，逻辑坐标不连续，无法直接组织ADT树，导致格心单元搜索区域在计算域内不完整，不能正确搜索落入分区边界附近的点，如图中点P.若在原网格系统下封闭格心区域，数据结构复杂，且对各种分区边界处理十分繁琐.文献［12］采用面、线、点顺序延拓的方法，重构分区边界的插值关系，但该方法只解决了完全封闭的计算域内部拓扑，对延拓部分没有形成理论描述.

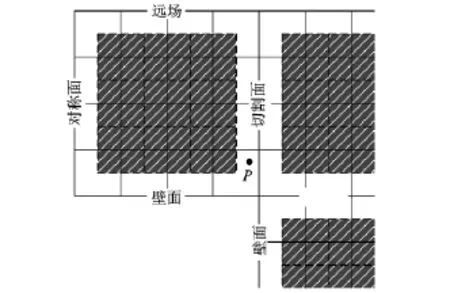
图1 各子区格心单元覆盖区域(虚线围成阴影)

1.2 虚网格边界

本文借鉴CFD计算格式对边界处理的方法，引入虚网格的思想，较好解决了格心网格下ADT树封闭问题.虚网格由计算域内格心网格向外扩展得到，图2是二维的虚网格示意，与图1情况比较，虚网格在分区边界的扩展，填补了原格心单元各子区之间的“空白地带”，确保搜索空间内部完整封闭.除分区边界外，其余类型边界也扩展了虚网格，使虚网格单元的实际覆盖面积大于计算域，在下文中将介绍，非分区边界虚网格不作为有效贡献单元，仅在重叠过程中临时使用.

图2 二维虚网格示意

虚网格中包含边界条件信息，如由远场边界外推的虚网格记为“远场”，其余亦然.对边界搭接的角点，如图2中点(0，JN)，同时在远场和对称面上，则不标记边界属性.边界附近寻点结果包含明确的边界信息，对重叠过程中正确处理寻点结果有重要意义，如挖洞结束时，洞面点P1可能落在壁面和第1层格心网格之间，传统方法搜索结果是无贡献单元，且无具体信息，程序无法区分P1点与远场外P2点，可能错误地解读为洞边界已远离物面，使重叠出错.由本文方法在计算域中(尤指边界处格心域小于计算域的情况)均能直接找到顶点含虚网格的贡献单元，状态由虚网格边界属性确定，为重叠过程中正确处理寻点结果提供有效信息.

使用Stencil Walk方法寻点时，网格点在单一边界附近有时也能提供边界信息，但位于多个边界搭接处时，Stencil Walk方法由初始位置出发，到第1个边界处，不论是否找到贡献单元都会停止移动，并记录停止处单一边界信息.如图2中点P4，Stencil Walk方法搜索结果是无贡献单元，边界信息可能是“远场”附近，也可能是“对称面”附近，由移动过程不可预测地决定.而在重叠过程中，远场和对称面附近寻点结果意义是不同的.因此，Stencil Walk在边界附近寻点存在隐患，可能存在合理贡献单元但因边界约束而无法正确查找，或者如前所述无法提供寻点结果的正确边界信息.使用本文方法时，P4点可以直接找到顶点含虚网格的贡献单元，虚网格包含“远场”和“对称面”信息.

1.3 虚网格构建

明确的边界定义使计算虚网格物理坐标时可以根据其边界属性相应处理.远场、壁面和对称面等非分区边界，虚网格不作为有效贡献单元，无需计算准确的位置信息，可以直接由内层网格线性外插获得.一些情况下外插的网格可能出现扭曲或变形，由于ADT方法对包围盒搜索，只关注目标物理坐标上下限值，与结构的几何细节无关，故虚网格的扭曲或变形对ADT的搜索结果没有影响.

分区边界附近计算跨区单元顶点是建立格心网格ADT搜索体系的难点.在两个子区对接的简单情况下，若虚网格有对应的实网格(相邻分区第1层格心网格)，则使用该实网格位置信息以构成有效贡献单元，且在重叠过程中虚网格属性始终指向该实网格.

多个子区连接时，格心单元跨越多个子区，搜索单元顶点十分繁琐，虚网格的定义较大简化了处理方法.分两种情况讨论:

1)图3a所示计算域内部有子区紧密连接时，由P1搜索对角线顶点P4，从P1出发，沿P1—P2—P3—P4或 P1—P5—P6—P4或其他任一条路径(共有6种最短路径)通过穿越分区边界搜索相邻实网格，均能获得顶点P4的正确信息;

2)(二维示意可参考图2中CELL1单元)如图3b所示，跨区格心单元有非分区边界顶点P6，此时沿P1—P5—P6—P4搜索，由于P6和P4逻辑坐标没有关联，搜索将中断，只有沿特定路线如P1—P2—P3—P4，才能正确获得顶点P4信息.

搜索路径的选择与算法有关，但对不同的拓扑情况和分区逻辑坐标顺序不同，执行时有较大的不确定性.一种做法是对所有可能的路径都进行分析，判断跨区单元的虚网格顶点是否有对应的实网格，但这显然不是一种好的做法.由本文方法对虚网格的定义，注意到顶点含非分区边界虚网格的格心单元不是有效贡献单元，该单元只使用边界信息，不需要准确的位置信息.因此在搜索路径中，若出现非分区边界，跨区单元的该顶点可由线性插值近似获得，无需严谨寻找或有的对应实网格，有效简化了复杂分区边界上跨区单元顶点搜索的算法.

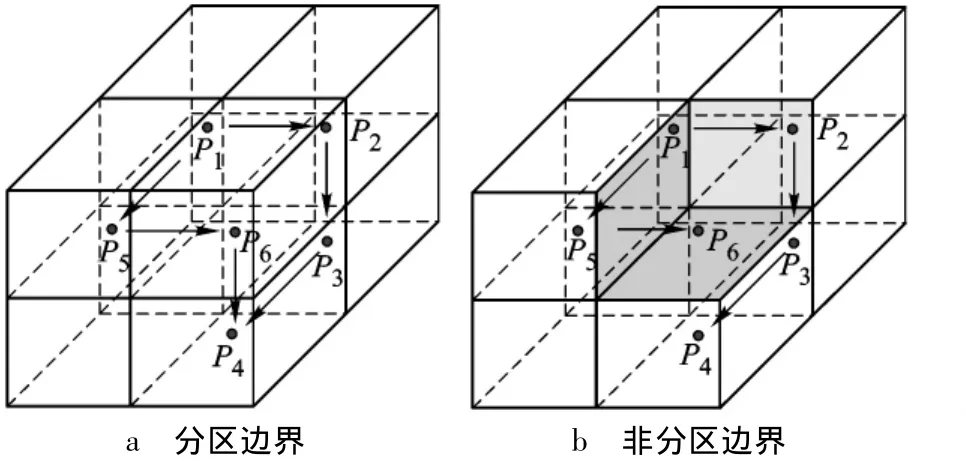
图3 边界上搜索跨区单元顶点

1.4 对称面处理和扩展的patch面

本文方法的一个重要应用是可以在对称边界上进行寻点，扩展了可处理的边界类型.

先讨论传统方法处理对称边界遇到的困难，图4是半模弹身在背景网格中的截面示意，模型中包括壁面、远场和公共的对称面边界.对于格点系统，弹身网格和背景网格在对称边界上重合，格点单元均有效覆盖半模空间.但在格心系统中，由于对称面附近网格尺寸不同，两物体对称面格心网格线相贯，弹身格心单元的实际覆盖区域小于背景网格，即意味背景网格在对称面附近部分网格落在弹身网格域外，传统方法寻点将找不到贡献单元，不能作为插值点使用，如图中格心网格线IS1上端位于弹身远场外，是正常点，IS1下端被弹身物面挖去，是洞内点，而中间没有可作重叠边界的有效插值点，将导致计算中流场信息错误地在洞外区域和洞内区域传递，使计算结果错误甚至发散.

图4 半模弹身在背景网格中示意

图4所示情况只是对称面寻点的一种，对多个物体重叠，或者对称面附近网格相对关系变化大时，问题更加复杂，但原因均是各物体格心单元覆盖的半模空间不完整，使对称面附近ADT搜索区域有缺失，导致部分网格不能相互找点.虚网格的引入解决了上述问题，图5是按本文方法扩展后的网格体系示意，在弹身和背景网格对称面上各外推一层虚网格，由虚网格和实网格组成的单元集合完整地覆盖了半模空间，使对称面附近任一实网格均能搜索到贡献单元.贡献单元顶点中或包含虚网格，程序中作如下处理:

1)网格重叠过程中，只使用贡献单元中实网格属性作为洞边界移动的判据，虚网格提供确保ADT搜索成功的完整空间;

2)重叠结束后建立插值边界，若贡献单元顶点含虚网格，则置换为相邻的实网格单元，以与求解器匹配，此时插值点在实网格单元外部，插值系数在(0，1)区间外，但一般情况下对称面附近网格匹配较好时，插值系数溢出很少.

图5 半模弹身在背景网格中的虚网格扩展

与对称面寻点类似，若有两个边界面贴合在一起，传统方法的处理也存在寻点失败的问题.图6a是超音速来流条件下，弹身前体在背景网格中示意，模型中有公共的后场面，与上例类似的是后场上格点网格共面，格心网格位置交错，使后场附近寻点搜索空间不完整.本文方法处理时，给后场网格面建立新的边界类型“patch”，表示有网格面在此处贴合.图6b是扩展后的网格体系，虚网格由相邻实网格线性外推，用于封闭搜索空间，使寻点在后场附近能有效执行.程序中对顶点含“patch”虚网格的贡献单元处理与对称面情况一致.

图6 前体在背景网格中的网格示意

2 算例研究

本文发展的寻点方法已在 MI-GRID［11，13-14］中得到应用.MI-GRID是北航阎超课题组研制的重叠网格软件，从2000年开始研制，目前仍在不断改进和发展.该重叠网格软件计算效率高、可靠性好，先后参与了国内多个航空航天型号研制工作，包括复杂外形飞行器、子母弹抛撒、助推级分离、折叠翼打开等项目，得到了有效考核.

为验证本文发展的方法，对美国大力神四号(TitanⅣ)大型捆绑式运载火箭的超音速绕流问题［15］进行数值模拟研究，计算条件为:M∞=1.6，ReL=1.1 ×107，α =0°.分别生成芯级和助推级的半模计算网格，网格数目为190万和40万.算例在配置INTEL CORE2 Q8200，2 GB内存的微机上运行，经测试，格点搜索法和格心搜索法生成ADT树所需存储开销相当，但格点法在查找中需执行大量Stencil Walk操作，故执行时间要稍多于格心法.

图7是TitanⅣ运载火箭半模模型示意，模型中包括公共的对称面和后场patch面.图8是重叠结果，在对称面和patch面上重叠边界整齐、重叠形式合理，说明本文方法在复杂边界条件下能正确应用.

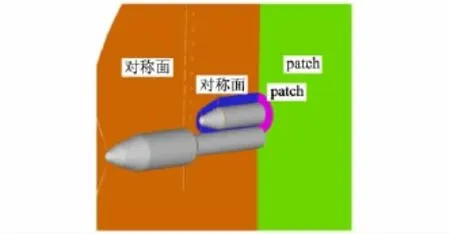
图7 半模模型的边界类型

图9是火箭芯级中心线上的压力分布与实验的比较，计算结果与实验值吻合较好.因为在风洞实验中，芯级与助推级间存在连接机构，导致实验的峰值点略高.

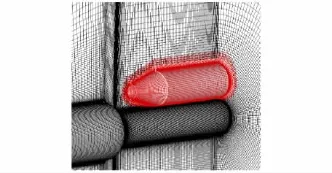
图8 半模模型重叠网格示意

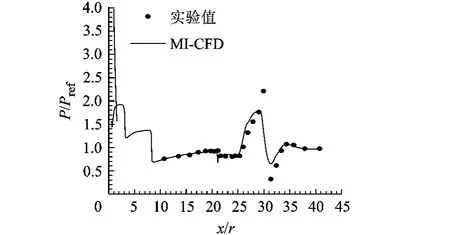
图9 芯级中心线压力分布

3 结论

本文提出了一种直接在格心网格下操作、基于虚网格边界的ADT搜索方法，研究结果表明:

1)通过扩展虚网格，使格心网格覆盖区域完整封闭，成功实现格心网格下的ADT数据结构.与格点搜索法相比，格心搜索法直接给出贡献单元可能的解集，再进行局部遍历，完全摒弃了不稳定的Stencil Walk方法，有效提高了寻点方法的可靠性.

2)虚网格边界的定义使寻点在边界附近的处理更为灵活，可以准确给出边界附近贡献单元的有效信息，同时，有效简化了虚网格系统的构建，尤其是简化了各种复杂拓扑下分区边界附近跨区单元顶点的搜索算法.

3)虚网格的重要应用是扩展了重叠边界类型，传统方法处理对称面时存在理论缺陷，新方法创建的搜索集合能完整覆盖网格空间，解决了对称面重叠问题.

References)

［1］Steger J L，Dougherty F C，Benek J A.A Chimera grid scheme［C］//ASME Mini-Symposium on Advances in Grid Generation.Houston:［s.n.］，1982:59 －69

［2］Ralph W N，Jeffrey P S.A summary of the 2004 overset symposium on composite grids and solution technology［R］.AIAA-2005-921，2005

［3］Sudharsun Jagannathan.A methodology for assembling overset generalized grids［D］.Mississippi:Mississippi Computational Engineering in the College of Engineering，Mississippi State University，2004

［4］Sogers S E，Suhs N E，Dietz W E.PEGSUS 5:an automated preprocessor for overset-grid computational fluid dynamics［J］.AIAA Journal，2003，41(6):1037 －1045

［5］Prewitt N C，Belk D M，Shyy W.Parallel computing of overset grids for aerodynamic problems with moving grids［M］.Gainesville:［s.n.］，1999:117 －172

［6］Morgan P E，Visbal M R.Chimera-based parallelization of an implicit Navier-Stokes solver with applications［R］.AIAA-2001-1088，2001

［7］Belk D M，Maple R C.Automated assembly of structured grids for moving body problems［R］.AIAA-95-1680-CP，1995

［8］Meaking R L.A new method for establishing intergrid communication among systems of overset grids［R］.AIAA-91-1586，1991

［9］Bonet J，Peraire J.An alternating digital tree(ADT)algorithm for 3D geometric searching and inter-section problems［J］.International Journal for Numerical Methods in Engineering，1991，31(1):1－17

［10］Spinetti R L，Jolly B A.Time-accurate numerical simulation of GBU-38s separating from the B-1B aircraft with various ejector forces，store properties，and load-out configurations［R］.AIAA-2008-187，2008

［11］李亭鹤.重叠网格自动生成方法研究［D］.北京:北京航空航天大学航空科学与工程学院，2004 Li Tinghe.Investigation of chimera grid au-tomatic generation algorithm［D］.Beijing:School of Aeronautic Science and Engineering，Beihang University，2004(in Chinese)

［12］王建涛.直升机旋翼前缘下垂控制动态失速数值模拟研究［D］.绵阳:中国空气动力研究与发展中心研究生部，2008 Wang Jiantao.Numerical simulation of dynamic stall control on helicopter rotor wings with variable droop leading edge method［D］.Mianyang:Graduate School，China Aerodynamics Research and Development Center，2008(in Chinese)

［13］阎超.计算流体力学方法及应用［M］.北京:北京航空航天大学出版社，2006:200－220 Yan Chao.The methodology and application of computational fluid dynamics［M］.Beijing:Beihang University Press，2006:200－220(in Chinese)

［14］范晶晶.复杂重叠网格方法研究及多体运动的非定常流动模拟［D］.北京:北京航空航天大学航空科学与工程学院，2010 Fan Jingjing.Enhancement of complex overset grid assembly and numerical simulation of unsteady multi-body movement［D］.Beijing:School of Aeronautic Science and Engineering，Beihang University，2010(in Chinese)

［15］Stephen Taylor，Johnson C T.Launch-vehicle simulations using a concurrent，implicit Navier-Stokes solver［R］.AIAA-95-0223，1995