基于改进粒子滤波的PSK信号时延和码元联合估计算法

夏楠，邱天爽

（大连理工大学 电子信息与电气工程学部，辽宁 大连 116024）

1 引言

移相键控(PSK)调制是通信系统中应用广泛的一种数字调制方式。在信号传输过程中，受到无线信道等因素的影响，使得信号本身产生时间延迟、幅度衰减、载波频率和相位的偏移。在接收端对信号进行解调之前需要估计这些未知参数并对其进行补偿，否则解调性能将受到严重的影响。文献[1]通过接收端观测信号的相关信息，恢复出上述未知参数。但是，实际中无法获得同步参数的最佳估计器，因此很多现有的算法都是基于最大似然近似理论。

近些年来，粒子滤波算法越来越引起广泛的关注，其基本思想是构造回归的贝叶斯滤波器并通过蒙特卡洛实验估计后验概率密度函数(pdf)。进一步可以理解为通过用状态空间中未知状态的随机采样点及相应权值来近似概率分布[2]。与卡尔曼滤波及其改进算法相比[3,4]，粒子滤波算法同样需要构造状态方程与观测方程。但是，对于非线性或者非高斯环境下，粒子滤波算法能够提供一种更为方便、有效的方法。因此很多国内外学者将粒子滤波算法应用到通信信号参数估计与码元检测中[5～8]。文献[5]提出基于粒子滤波相位跟踪算法，并通过二阶数字锁相环技术实现相位的无偏估计。文献[6]提出一种基于粒子滤波的自适应盲时间延迟和码元的联合估计方法，并给出接收端开路和闭路结构。文献[7]将粒子滤波算法运用到无线传感器网络节点与目标的联合定位问题。文献[8]提出一种基于粒子滤波的时变信道盲均衡算法。本文重点对文献[6]中的算法进行深入研究。文献[6]通过估计时间延迟参数来实现信号检测,而时间延迟可以看作是非时变参数。对于非时变参数的估计问题，随着粒子滤波算法的不断进行，重采样过程会导致错误的后验概率分布，进而降低估计的精度。解决该问题的方法是在参数迭代的过程中引入一个抖动，可以理解为叠加一个状态噪声[9]。但是，对于算法的每一次迭代，都需要叠加状态噪声。如果噪声过小，同样会出现上述问题，而如果噪声过大，则会出现无法收敛的情况，这都会导致估计精度下降。

本文提出一种自适应重采样方法，根据迭代误差的变化，动态调整状态噪声的方差。当算法尚未收敛时，使噪声方差较大，这样可以使粒子尽量准确地描述后验概率分布，而当算法收敛时，使噪声方差较小，可以有效地提高估计精度。另外，通过分析发现，对于较小的时间延迟，文献[6]算法的估计误差较大。本文提出一种基于粒子滤波的正向与反向结合的码元检测算法，有效地解决了这一问题。通过计算机仿真，将改进算法与文献[6]的算法进行比较，并对性能做以分析。

2 信号模型及问题描述

2.1 信号模型

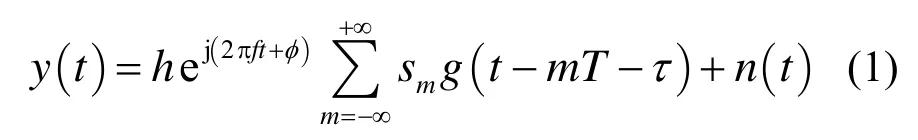
考虑经过本地振荡器后，接收机前端接收到的经过匹配滤波后的BPSK基带信号，用复数形式可表式为其中，hejφ表示信道参数，并且本文假设其已知，f表示信号载波频偏，sm∈{-1 ,1}为传输的码元序列，其符号率为（T为符号周期），M为传输的码元个数，τ为信号的时间延迟，这里τ∈(0,T)，g(t)表示升余弦波形信号，n(t)是均值为0，方差为σn2的高斯白噪声。对信号y(t)按符号率1T进行采样，将结果以矢量的形式表示为

2.2 状态空间模型

为了运用粒子滤波方法来递推估计未知参数和符号序列，需要建立状态空间模型，即状态方程。假设在一段时间内时间延迟及载波偏差保持不变，则有

其中，vτk与vkf是均值为0，方差分别为στ2和σ2f的高斯白噪声，dk=[0,… ,0 ,sk+L]T为2L× 1 扰动矢量，sk+L为需要估计的码元，

为22LL×转移矩阵。

2.3 粒子滤波算法

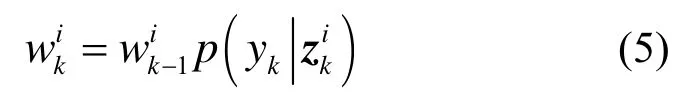
p可由状态方程式(3)得到，可表示为

在已知粒子初始分布的前提下，通过算法自身迭代与粒子重采样过程[10,11]，获得新的粒子和重要性权重，进而得到状态变量的估计。该算法给出最小均方误差估计量(MMSE)对时间延迟τk和频偏fk的估计，即

对符号序列的最大后验概率估计，即

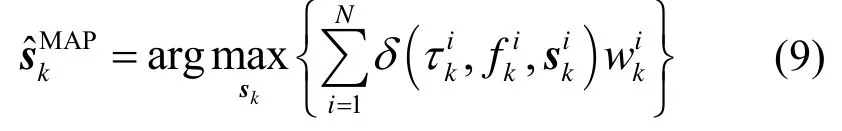
3 算法改进

3.1 问题描述

时间延迟估计可以看作是非时变参数估计问题。粒子滤波算法能否实现非时变参数的精确估计，在某种程度上取决于粒子的初始分布的选择是否合适。如果待估参数的真实值存在于初始分布中，那么随着算法的进行，会检测出权值较大的粒子，即在数值上接近于真实值的粒子。通过重采样算法，那些权值可以忽略的粒子，则会被大粒子所取代，然后通过最小均方误差准则对参数进行估计，能够得到较好的结果。但是，在很多情况下，无法预知粒子的先验分布，或者只能够确定一个很大的范围。在这种情况下，随着算法的进行，可能会出现所有粒子的权重都非常小，算法会收敛到一个错误的结果或者不收敛，进而使算法失效。解决这一问题，可以从两方面来考虑。一方面可以增加粒子的数量。由于人为设置的粒子初始分布范围很大，需要大量的粒子，才能够使得部分粒子在数值上接近于参数的真实值。但是这样会大大增加算法的复杂度，实际意义不大。另一方面可以引入状态误差。文献[6]通过在迭代过程中，对于时间延迟，人为地加入较小的随机抖动，使得非时变参数估计转化为时变参数估计问题。这样做的意义在于当初始分布的选择不合适而粒子数量又相对较少时，通过引入一个随机抖动，可以使得部分偏离真实值的粒子向真实值靠拢。这样，算法不会因为粒子的衰退而失效。但是，对于如何设置随机噪声的方差，却无法衡量。方差设置过小，同样会出现粒子衰退的问题；如果方差设置过大，会使算法不收敛。这样就需要一种自适应的方法动态调整方差大小，进而可以使粒子更好地近似概率分布。

在码元检测方面，文献[6]中考虑到实际情况中为防止码间干扰而引入成型滤波器，而且成型滤波器一般选择升余弦滤波器。因此在观测方程式(2)中出现码元矢量和升余弦波形信号采样矢量相乘的形式。文献[6]同时给出了粒子滤波平滑算法，因为在滤波器系数矢量中，有些系数很小，对码元检测结果影响不大，因此可以忽略。图1给出滤波器系数，其中，L=2，且

图1 升余弦滤波器时域波形

3.2 粒子滤波改进算法

在3.1节中，针对文献[6]存在的问题进行了分析，这一节中将给出具体的改进方法，提出针对时间延迟估计的自适应采样法和码元正向、反向检测法。

3.2.1 自适应重采样

自适应采样法通过调节迭代过程中状态噪声方差，使得当算法没有收敛时，加入较大状态噪声，这样粒子能够更准确的近似概率分布；而当算法收敛时，加入较小状态噪声，使得估计精度更高。文献[12]对粒子滤波算法的收敛性进行了详尽的证明，并给出2阶收敛于最优估计器的结论。这里只给出其简化表达式，有

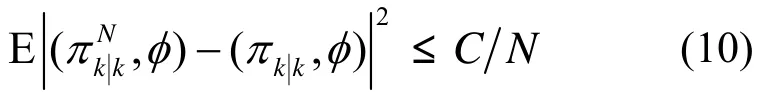
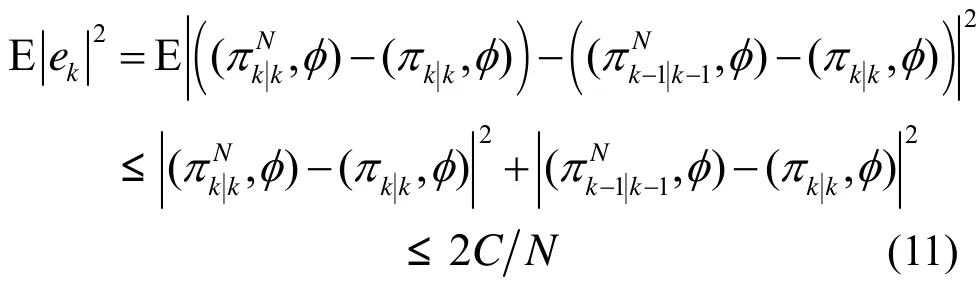
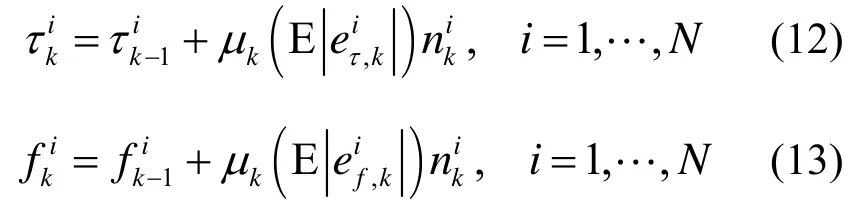
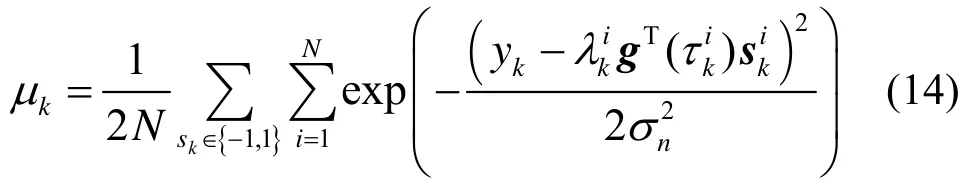
3.2.2 码元反向检测

码元反向检测算法是通过观测数据由后至前地检测出码元序列，其目的在于当时间延迟较小时，赋予待检测码元较大的权重。由此，获得新的码元矢量k′s、扰动矢量k′d和转移矩阵′S，分别为

依照式(3)给出码元序列的状态方程，有

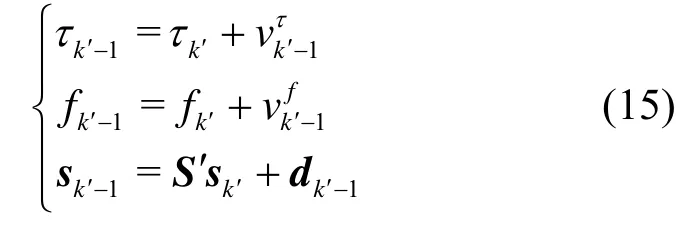
当时间延迟较小时，会使g( -T+τk′)较小，而g（τk′）较大，这样在矢量相乘的过程中，码元sk′会获得更大的权重，从而实现码元的反向检测。得到该算法的权重更新方程，有

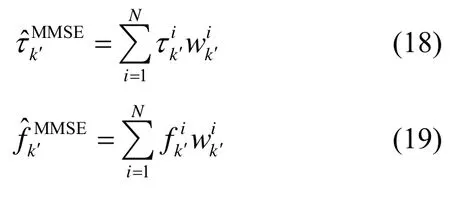
该算法仅为较小时间延迟提供有效估计，对于较大时间延迟仍需要采用文献[6]中的方法，即码元正向检测。通过以上分析，不难看出，对于正向检测来说，不管时间延迟真值分布在哪个区间，估计结果都会是同理，对于反向检测来说，时间延迟的估计结果都会分布在换句话说，时间延迟较小的正向检测和时间延迟较大的反向检测都会使估计结果与实际不符，但是对于参数盲估计问题，无法预知时间延迟的大小，只能根据经验得到其大概分布范围，满足时间上0到T的均匀分布。因此，在开始阶段，需要正向检测算法与反向检测算法并行使用，当获得正确的时间延迟之后，对观测信号进行同步并按照符号率进行采样。如果时间延迟估计的准确，经过同步后，会得到不受码间干扰影响码元序列或者，否则，干扰仍然存在。该方法的结构如图2所示。在算法初始阶段，按照k=L, … ,M-L和k′ =M-L, … ,L分别对观测信号y(t)进行抽样，经过正向和反向粒子滤波算法后，得到时间延迟估计和。通过对观测信号进行同步并进行重抽样，然后对此两路信号先后取绝对值和均值，并对结果m1和m2进行大小比较。比较器输出来控制开关，从而选择结果较大的一路来完成剩余码元的检测。由成型滤波器原理可知，若时间延迟估计得准确，则同步后会消除码间干扰的影响，否则，码间干扰会继续存在。选择取绝对值是为了消除符号的影响，选择取均值一方面是消除观测噪声的影响，另一方面考虑到时间延迟估计不正确的一路，会因为受码间干扰影响而使其均值小于另外一路。然后通过均值大小来决定应采取正向检测法还是反向检测法。当选择正确的码元检测方向之后，可以通过开关控制另外一路检测停止。此时，会得到同步后无码间干扰的码元序列或者。同时，为消除载频偏差的影响，需要对接收信号进行载频补偿。本文算法具体流程如算法1所示。

螺钉断裂8例，7例发生于术后4 ～ 6个月，其中5例出现胸腰部疼痛，行开放手术翻修并增加伤椎固定螺钉，随访12个月骨折愈合良好；2例无明显不适采用胸腰背支具保护定期复查，术后12 个月骨折愈合良好拆除内固定。1例发生于术后8个月，行腰椎CT检查，明确骨折愈合行内固定取出。

图2 本文算法结构

算法1 本文算法流程

初始化粒子τ0～U（ 0,T） ，f0～U（ -fmax,fmax）

当k=L:M-L和k′ =M-L:L(M是符号数量)

当i= 1 :N(N是粒子数量)

根据文献[11]中算法进行粒子重采样。

根据式(7)、式(8)、式(18)和式(19)，分别估计时间延迟和以及载频偏差和。

比较m1和m2并检测码元。

4 实验仿真

为验证改进算法，考虑使用BPSK信号。采样频率为fs= 5 0MHz ，码元周期T= 1 μs，载频偏差fmax= 1 kHz 成型滤波器采用滚降系数为0.9的时间有限升余弦滤波器，且L=2。通过仿真实验发现，码元序列长度M＞200以及粒子数量N＞300时，均能达到较好性能指标。因此在本文仿真实验中，兼顾计算量和算法性能的要求，选取M=500个码元和N=300个粒子进行处理。如果没有特殊说明则信噪比为10dB。

首先将经过载频偏差补偿及自适应重采样的粒子滤波算法与文献[6]中算法在不同状态噪声方差下进行对比。由于文献[6]的正向检测算法，对时间延迟失效，因此，这里仅对的情况进行仿真，并采取归一化最小均方误差(NMSE)准则进行评估。时间延迟kτ的归一化最小均方误差可表示为其中，Q表示独立实验的次数，这里进行Q=100次仿真实验。图3得到不同信噪比下时间延迟最小均方误差估计。可以看到，与固定状态噪声方差的方法相比，采用自适应重采样的粒子滤波算法，在相同信噪比条件下最小均方误差明显降低。并且信噪比SNR＞10dB时，都能够获得较高的估计精度。

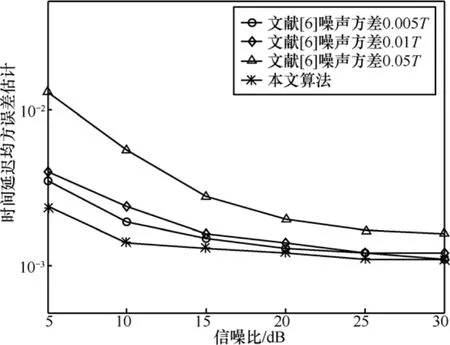
图3 自适应重采样与原算法的时间延迟的均方误差估计

然后，考察在不同时间延迟情况下，本文算法中正向检测与反向检测的判决分析，即对图 2中m1和m2进行对比，并给出时间延迟估计结果和。同样选择独立实验次数Q=100，得到m1、m2、和的100次统计平均结果，如表1所示。可以看出，当时间延迟τ≤ 0 .1T、τ≥ 0 .9T或者取值在0.5T附近，都会使m1和m2较为接近。这时虽然无法准确判断用正向还是反向对码元进行检测，时间延迟估计也不一定准确，但是对观测信号进行同步并重采样之后，受到码间干扰非常小，基本可以忽略，因此对码元检测没有影响。当时间延迟分布在其他区间时，根据m1和m2的大小选择正确的检测方向，并用时间延迟估计结果对观测信号进行补偿，可以消除码间干扰的影响。

图4 较小时间延迟估计结果对比

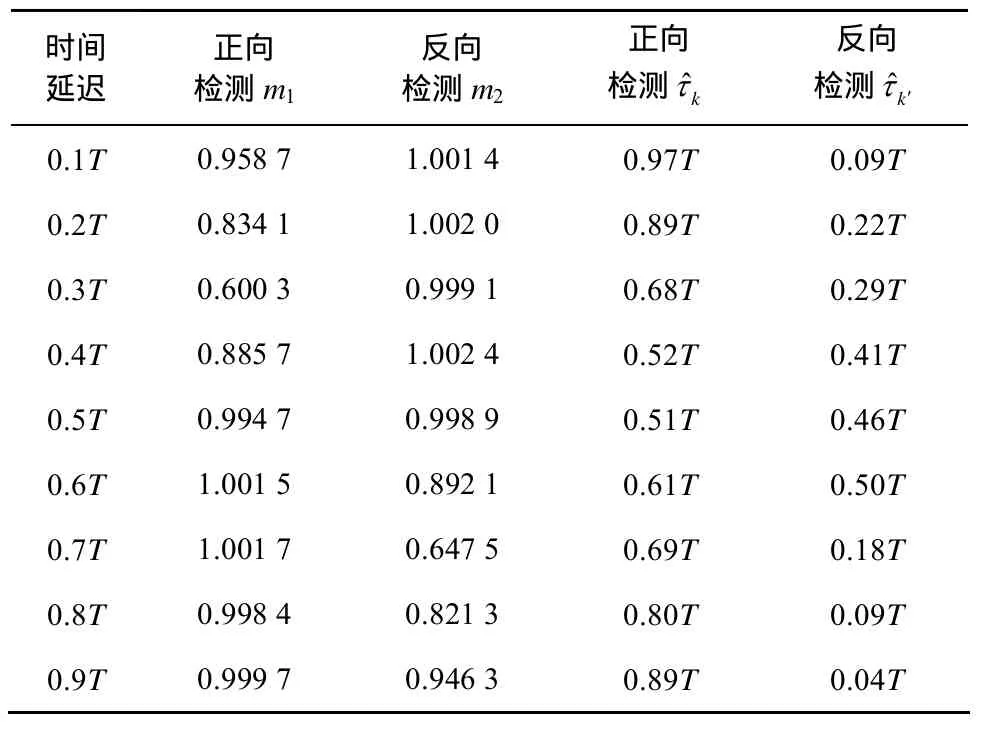
表1 正向检测与反向检测对比

最后，分别给出在相同条件下，文献[6]中算法和本文算法的误码率曲线。仿真中采用自适应重采样以及正向、反向码元检测相结合的方法。码元长度M=500，粒子数量N=300，独立实验次数Q=100，且每次实验在(0, T)区间随机产生时间延迟真值。在接收端对载频偏差进行补偿。由图5可以看到，由于克服了时间延迟估计失效的问题，本文算法在性能上明显优于文献[6]中的算法。

图5 误码率随信噪比变化曲线

5 结束语

本文对基于PSK信号时间延迟估计的粒子滤波算法进行了深入的研究，并对原算法进行了改进。提出一种通过自适应计算状态噪声方差进行粒子重采样的方法。该方法能够有效消除状态噪声方差人为设置过大或者过小对估计结果的影响。同时还提出一种基于码元反向检测的时间延迟估计方法。该方法与原方法相结合，可以实现对于(0,T)范围内时间延迟的精确估计。另外，本文考虑载波频率偏移的影响，利用粒子滤波算法对其进行估计并补偿。通过计算机仿真验证了本文算法的有效性。同时，该算法还可以应用到其他数字调制信号的参数估计和码元检测问题上，具有较强的推广价值。与此同时，多参数估计或者多路码元序列检测问题是今后需要解决的问题。

[1] MENGALI U, D’ANDREA A N. Synchronization Techniques for Digital Receivers[M]. New York: Plenum, 1997.

[2] DOUCET A, FREITAS N D. Sequential Monte Carlo Methods in Practice[M]. New York: Springer, 2001.

[3] KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 8(2): 35-45.

[4] SALMI J, RICHTER A, KOIVUNEN V. Detection and tracking of MIMO propagation path parameters using state-space approach[J],IEEE Transactions on Signal Processing, 2009, 57(4): 1538-1550.

[5] KANDEEPAN S, EVANS R J. Bias-free phase tracking with linear and nonlinear system[J]. IEEE Transactions on Wireless Communications, 2010, 9(12): 3779-3789.

[6] GHIRMAI T, BUGALLO M, MIGUEZ J. A sequential Monte Carlo method for adaptive blind timing estimation and data detection[J].IEEE Transactions on Signal Processing, 2005, 53(8): 2855-2865.

[7] WANG X, AGGARWAL P. Joint sensor localization and target tracking in sensor networks[J]. IET Radar Sonar and Navigation, 2011,5(3): 225-233.

[8] GUIMARAES A, AIT-EL-FQUIH B, DESBOUVRIES F. A fixed-lag particle smoother for blind SISO equalization of time-varying channels[J]. IEEE Transactions on Wirless Communications, 2010, 9(2):512-516.

[9] DOUCET A, GODSILL S J. On sequential Monte Carlo sampling methods for Bayesian filtering[J]. Statistics and Computing, 2000,10(3): 197-208.

[10] LIU J, CHEN R. Sequential Monte Carlo methods for dynamic systems[J]. Journal of the American Statistical Association, 1998, 93(443):1032-1044.

[11] KITAGAWA G. Monte Carlo filter and smoother for non-Gaussian nonlinear state space models[J]. Journal of Computational and Graphical Statistics, 1996, 5(1): 1-25.

[12] CRISAN D, DOUCET A. A survey of convergence results on particle filtering methods for practitioners[J]. IEEE Transactions on Signal Processing, 2002, 50(3):736-746.