基于神经网络的地铁牵引整流器控制算法研究＊

杜荣茂，李向葵，景利学

（1 兰州交通大学 自动化与电气工程学院，甘肃兰州730070；2 甘肃省高等学校招生办公室，甘肃兰州730030）

随着我国经济的发展，传统的交通方式已经越来越不能满足城市居民高频率出行和城市交通发展的需要，而地铁交通可以缓解大城市交通拥堵的状况，因而目前许多大城市已开始考虑和策划修建地铁交通体系。城市地铁牵引供电系统采用传统整流方式获得750V或1.5 kV的直流供电方式，直流电压在交流电网侧存在大量的无功和谐波，因而对电网造成严重的污染。PWM整流器具有交流侧电流谐波含量小，功率因数高，能量双向流动等突出优点，因而在AC／DC功率交换中得到了广泛应用［1］。另外，地铁列车的运行工况十分特殊，地铁车辆在实际运行中有着频繁的加减速运行，使得地铁车辆所需的电流是不断变化的，因而难以建立精确的数学模型，应用常规PID控制器不能达到理想的控制效果。

人工神经网络具有很强的信息综合、学习记忆和自学习、自适应能力，可以逼近任意非线性函数，适合处理那些难以用模型和规则描述的过程，在一些不确定系统的控制中已成功应用。因此，将神经网络与PID控制结合可取得更好的控制效果。这方面国内外学者进行了大量的研究，提出了很多改进方法。有学者提出一种将神经网络与PID控制相结合的方式，即在常规PID控制器的基础上增加一个神经网络，用神经网络在线调整PID参数［2］。该方法虽然在整流器控制方面收到了较好的效果，但由于结构复杂且未实现神经网络和PID控制规律的本质结合，影响了该方法的实际应用。

本文提出采用基于神经网络的复合型单神经元PID控制器对地铁直流牵引整流器进行设计。该控制策略融合了神经网络控制和常规PID控制各自的优点，既保持了PID控制简单、精度高的特点，又充分发挥了神经网络控制灵活、适应性强、快速性好的优点，仿真结果表明该方法能得到更好的控制效果。

1 单神经元自适应PID控制器

1.1 单神经元自适应PID控制系统的构成及其学习算法

用单神经元实现自适应PID控制的结构框图如图1所示［3］。图中转换器的输入反映被控过程及控制设定的状态，设r（k）为设定值，y（k）为输出值，经转换器转换成为单神经元学习控制所需要的状态量X1（k），X2（k），X3（k），这里

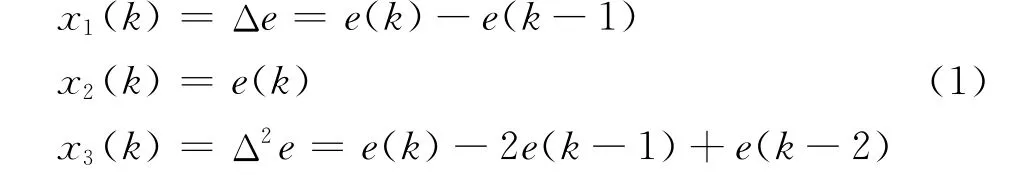
其中e（k）为误差函数；Δe（k）为误差变化率；k为时间变量。

图1 单神经元PID自适应控制器结构图

神经元通过关联搜索来产生控制信号，即

其中K为神经元的比例系数；Δu（k）为误差信号；w（k）为权值系数。

单神经元自适应控制器通过对加权系数的调整来实现自适应、自组织功能，单神经元的学习规则即加权系数的调整主要有3种［4］：无监督的Hebb学习规则、有监督的Delta学习规则和有监督的Hebb学习规则。本文采用的是最后一种学习规则，它与神经元的输入、输出和输出偏差三者的相关函数有关，因此采用有监督的Hebb学习规则时有：

式中ri（k）为递进信号；z（k）为输出误差信号；η为学习速率。由式（3）可得

式中Δωi（k）＝ωi（k＋1）－ωi（k）如果存在一函数fi（ωi（k），z（k），u（k），xi（k）），有

则式（4）可写为

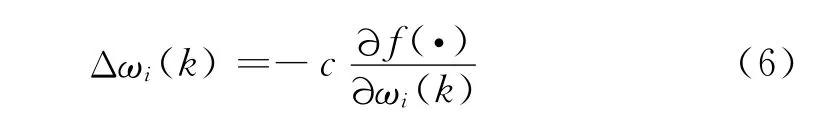
上式表明加权系数ωi（k）的修正按函数f（·）对应于ωi（k）的负梯度方向进行搜索。应用随机逼近理论可以证明当c充分小时，使用上述学习算法，ωi（k）可收敛到某一稳定值，且与期望值的偏差在允许的范围内。

为保证上述单神经元自适应PID控制器学习算法的收敛性和鲁棒性，对上述学习算法进行规范化处理后可得［5］：

比例系数K值的选取对控制性能影响很大，同时影响着动态响应和稳定性，这里对比例（P），积分（I），微分（D）分别采用了不同的学习速率ηp，ηI，ηD以便对它各自的权系数能根据需要分别进行调整，其取值由仿真与试验确定。

相对于常规PID控制算法而言，单神经元PID控制算法对给定信号的响应速度较慢，即上升时间较长，动态恢复缓慢［6］。因此形成了既有常规PID控制响应速度快的优点，又具有人工神经网络信息综合、学习记忆和自学习、自适应能力的复合型单神经元PID控制器。

常规PID的离散差分形式为［7］

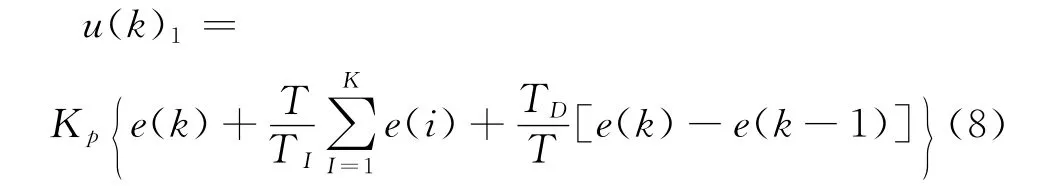
式中Kp为常规PID控制器比例系数；TI为积分时间，TD为微分时间。

通过单神经元关联搜索产生的控制信号为：

所以复合型单神经元PID的控制信号为：

由于本文研究的是运用于地铁的PWM整流器，微分环节只在系统启动阶段起到抑制超调的作用，在系统稳态运行阶段，微分环节对干扰过于敏感，还容易造成超调和系统振荡，因而我们只采用PI控制［8］。对于微分环节缺失可能造成的启动超调，由单神经元PID控制器进行补偿。复合型单神经元PID结构图如图2。

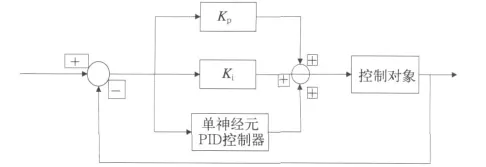
图2 复合单神经元PID结构图

1.2 复合型单神经元PID控制的电压外环的设计与仿真

神经元控制器的调节是非线性的自适应过程，只要在上面介绍的单神经元PID的基础上选择适当的学习速率η和神经元线性比例系数K，就可以使系统超调量小、无静差、对被控对象的参数及采样周期变化不敏感。

神经元有3个输入量Xi（t）（i＝1，2，3），转换器的输入反映被控制过程及控制给定的偏差状态。设定控制给定为yr（k），输出为y（k），偏差为e（k），经转换器后转换成为神经元学习所需的控制状态X1、X2、X3，其中Xl＝e（k），X2＝e（k）－e（k－1），X3＝e（k）－2e（k－1）＋e（k－2），本文中采用改进的Hebb学习规则，X1＝X2＝X3＝e（k）＋Δe（k）。

基于上面对单神经元PID控制器的了解，本论文通过MALAB软件编写单神经元PID控制器算法，重点研究将其运用于电压外环是否能够有效的稳定直流侧电压输出。令输入分别为U1、U2、U3。其中U1为给定的直流侧电压，U2为直流侧电压信号输出反馈，U3为时间轴，在 MATLAB／Simulink环境下的仿真逻辑图如图3：

图3 Matlab／Simulink环境下的仿真逻辑图

常规PI控制器KP设为2，KI设为200，则复合型单神经元PID仿真结构图如图4：

图4 Matlab环境下的复合型单神经元PID结构图

由以上分析我们确定了控制系统的实现方法为电压电流双闭环控制，电压外环作用通过复合型单神经元PID稳态无静差地跟踪给定，稳定直流侧电压输出。从对主电路模型的分析得出，直流侧电压输出由整流器三相网侧进线电流值决定，因此电压调节器的输出量可以作为电流跟踪内环的给定信号，通过解耦后的两个电流内环的跟踪调节，使网侧的进线电流值能够满足跟踪直流侧电压给定，并稳定直流侧母线电压的要求。由于我们期望得到单位功率因数，在具体实现上我们将两个经过处理过后独立的有功和无功电流单变量线性子系统分别进行设计，此时无功电流闭环子系统的给定为零，而有功电流闭环子系统的给定为电压调节器的输出，并且交流侧进线电流值的确定又与三相桥的网侧调制输出电压有关，因此两电流调节器的输出经过内环的附加前馈解耦处理后作为SVPWM调制的给定跟踪调制信号，通过SVPWM算法进行调制跟踪，从而完成了系统的稳定直流侧输出电压和功率因数控制，并且抑制了谐波电流的产生。实际上如果期望功率因数可调，则可以将电压调节器输出量经过功率因数计算模块后得出有功和无功电流的期望值，分别作为内环两电流调节器的给定，从而在稳定直流输出电压的前提下，达到功率因数可控的控制目的。

综上我们可以得到整个控制系统的控制逻辑图如图5所示。

如图中所示由电压检测环节将直流侧输出电压信号反馈回来与给定电压信号进行比较，通过PI调节器运算后作为电流内环中有功电流分量的给定信号。在三相电源的进线处的电流传感器将三相电流信号结合锁相环电路取得的A相电压的相位信息送入3S／2r变换电路，从而将三相电流信号分解为代表有功和无功的电流分量作为电流的反馈信号分别与电流内环的给定信号（作为电压调节器输出的有功电流分量给定和为达到单位功率因数运行目的而给定为零的无功电流给定信号）进行比较送入电流内环的PI调节器，内环的PI调节器的输出量经过控制系统注入的前馈和解耦量（前馈和解耦量的信息包含了交流侧电源电压矢量的信息和交流侧输入电流矢量的信息）后经过作3S／2r反变换生成的三相信号作为PWM桥交流侧实际输出三相电压的目标信号送入空间矢量控制器（SVPWM调制）后生成三相PWM桥的6只IGBT的控制信号，用来控制整流桥的交流侧实际输出电压跟踪给定信号，从而达到了整个整流装置在电压外环控制稳定直流电压输出，在电流内环跟踪给定电流信号使之波形接近正弦且与三相电压信号同相位，实现单位功率因数和减少谐波污染的控制目的。

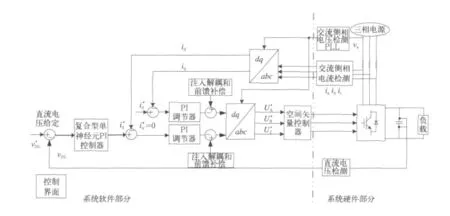
图5 控制系统的控制逻辑简图

2 地铁直流牵引供电系统测试与仿真

本论文基于MATLAB这个功能强大的仿真软件及其支持的仿真环境对三相PWM整流进行仿真研究。仿真参数：Em＝380V，Ls＝3.6mH，Rs＝0.2Ω，C＝2 350μF，KP＝0.6，KI＝100／3，Im＊＝±5V。

系统的控制算法由控制模块和SVPWM模块实现，电压、电流分别经检测模块输入到控制模块中，给定电压Udc＊和直流侧反馈电压Udc同时也输入到该模块中来，从而完成电压电流双闭环控制。

在控制模块中给定指令电压Udc＊与实际直流侧电压Udc比较后经复合型单神经元PI调节器得到电流有功分量指令，然后id＊、iq＊（iq＊给定为0）分别与交流侧实际电流有功分量和无功分量比较，经PI环得到指令电压Ud＊、Uq＊，经过电网电压、电感电压交叉分量的前馈补偿后，通过2／3变换模块合成电压矢量V＊，最后将该矢量输入SVPWM模块，输出便作为控制三相电压型SVPWM整流器的脉冲指令。

SVPWM模块和控制模块的仿真结构如图7所示。

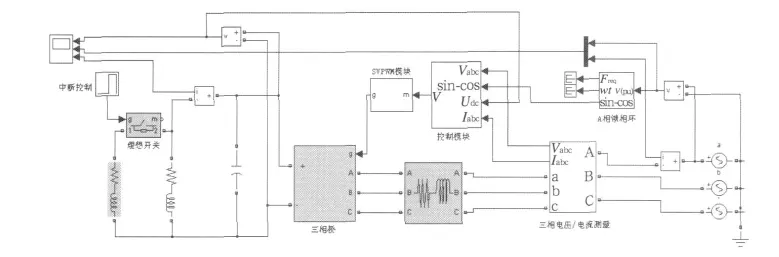
图6 地铁直流牵引整流器主电路仿真图

图7 SVPWM模块和控制模块的仿真结构图

2.1 基于复合单神经元PWM控制与单神经元PWM控制的地铁直流牵引供电系统的仿真比较分析

（1）基于常规单神经元PWM控制的系统启动波形分析

整流器直流侧接阻感负载（R＝10Ω，L＝0.01 mH），无功电流Iq为0，整流器工作在单位功率因数情况下启动。在阻感负载下启动直流侧电压、交流侧a相电压电流波形如图8所示。

由图形可知调节时间ts＝0.12s，直流电压超调量约为6.7%。

（2）基于复合单神经元PWM控制的启动波形分析

负载与上一仿真相同，且同为单位功率因数下启动，则启动时直流侧电压、交流侧a相电压、电流波形如图9所示。

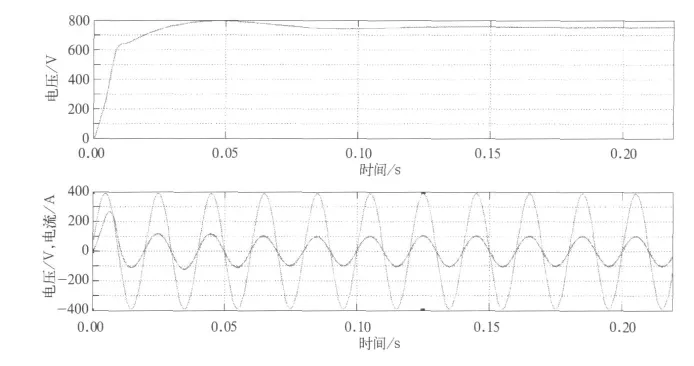
图8 基于常规单神经元PWM控制的系统启动直流侧电压、交流侧a相电压电流波形图

图9 基于复合单神经元PWM控制的系统启动直流侧电压、交流侧a相电压电流波形图

观察直流侧电压波形可知调节时间ts＝0.05s，直流电压超调量同样为6.7%，由此可以验证常规单神经元PID控制器确实存在上升时间较长，动态恢复缓慢的问题，而复合型单神经元PID控制器完全可以弥补常规单神经元PID控制器存在的问题，调节时间和超调量都非常令人满意。因此基于复合型单神经元PWM控制适用于地铁直流牵引供电系统。

2.2 基于复合单神经元PWM控制的系统交流侧id、iq分析

在与上以仿真相同的负载和仿真条件下，观察交流侧id、iq波形如图10所示。

有功电流在稳定后的值约为1.25A，无功电流在稳定后值为0A，说明整流器工作在单位功率因数情况下，从而验证了通过该方法控制PWM 整流电路，可以使功率因数近似为1，而从上一仿真交流侧电流波形可以观察，输入电流非常接近正弦波，且和输入电压同相位。

2.3 系统负载突变时的仿真分析

系统在0.105s时突加负载，在0.175s时突减负载，仿真波形如图11所示。

图10 系统交流侧id，iq波形图

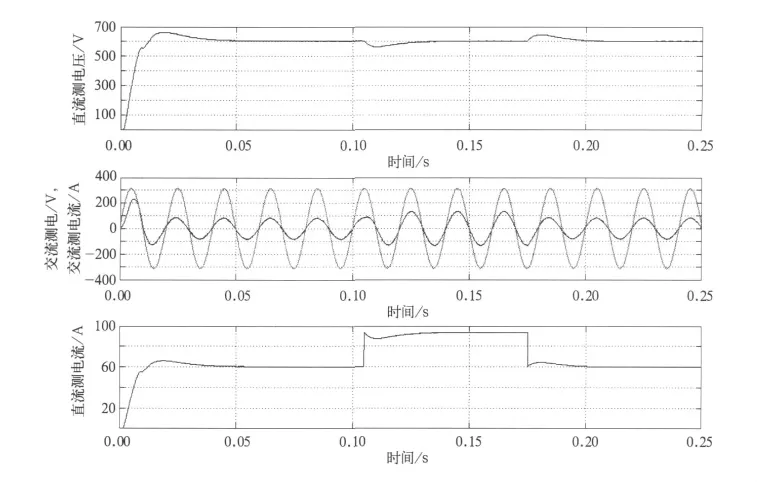
图11 系统负载突变时的仿真波形

从图中可以看到系统受到负载扰动恢复时间约为0.03s，输出直流电压的闪动约为4.5%，可见系统拥有较好的抗负载突变的能力，适用于地铁和轻轨列车经常需要频繁的起动、停车的条件。

3 结束语

本文在地铁直流牵引供电系统采用的三相PWM整流器的基础上，研究其控制策略并提出了将单神经元PID控制器运用于地铁供电整流器系统的新方法。本文设计了在两相旋转坐标系下的电压电流双闭环的矢量控制系统。其中内环为有功和无功电流分量在d－q坐标系下的解耦控制，而电压外环采用复合型单神经元PID代替传统PID稳定直流侧电压，并获得了传统PID所没有的信息综合、学习记忆和自学习、自适应的能力。同时用MATLAB中的Simulink工具箱对该系统进行了仿真，最后在Simulink环境下对系统进行了整体的仿真研究，分别观察了系统启动以及直流侧负载突变时的响应波形。仿真的结果证明按照上述控制策略，整流器具有接近单位功率因数为1，直流侧电压稳定，抗扰性能较好的优点。

［1］王晓东，奚国华，龙育才.中国特大城市轨道交通系统的研究与发展［J］.机车电传动，1999，40（3）：3－5.

［2］Y Ye，M Kazerani，V H Quintana.A Novel Modeling and Control Method for Three－phase PWM Converters.PESC.2001IEEE 32th Annual.2001，（1）：102－107.

［3］丁 军，徐用茂.单神经元自适应PID控制器及其应用［J］.控制工程.2004，11（1）：27－30.

［4］王俊国，王永骥，万淑芸.MATLAB环境下的单神经元自适应实时控制系统［J］.仪表技术与传感器，2004，（4）：21－29.

［5］M Malinowski，F Blaabjerg.Virtual－flux－based direct power control of three phase PWM rectifiers［J］.IEEE Trans on Industry Applications.2001，（6）：1019－1026.

［6］S Hansen，M Malinowski，F Blaabjerg，M P Kazmierkowski.Control strategies for PWM rectifiers without line voltage sensors.In proc［J］.IEEE－APEC Conf.2000，（2）：832－839.

［7］Mariusz Malinowski，Marek Jasiński，and Marian P.Ka－zmierkowski.Simple direct power control of three－phase PWM rectifier using space－vector modulation （DPCSVM）［J］.IEEE Tran.Ind.Electron.2004，（4）：447－453.

［8］张永昌，赵争鸣.基于快速空间矢量调制算法的多电平逆变器电容电压平衡问题研究［J］.中国电机工程学报，2006，26（18）：71－76.