制动盘摩擦面热损伤的形成机理分析*
2012-08-03杨智勇李志强李卫京韩建民
杨智勇,李志强,李卫京,陈 跃,韩建民
(北京交通大学 轨道车辆结构可靠性与运用检测技术教育部工程研究中心,北京100044)
在制动过程中,列车的动能通过制动盘和闸片之间的强烈摩擦转换成摩擦热,一部分摩擦热以对流和辐射的方式散入大气,大部分热量通过传导的方式输入到制动盘,输入制动盘的热量将导致制动盘温度升高,多次制动后将在制动盘摩擦面形成热损伤[1-5]。热斑、热裂纹和应力开裂是3种典型的制动盘宏观热损伤型式[6-7],如图1所示。

图1 热损伤类型
早在20世纪80年代,白以龙[8]在材料机械加工领域就发现了材料表面的温度集聚现象。A.J.Day[9]和M.Tir ovic[10]基于盘式制动器的压力分布的研究,认为闸片和制动盘之间产生的摩擦热并不是均匀地分布在滑动表面上,而是存在温度的集聚区域。制动盘摩擦面的温度集聚导致在其表层形成热斑,并在多次制动后,在摩擦面形成热裂纹。制动盘内部温度的不均匀分布,会在制动盘的内部形成热应力[11],国内外的研究者采用有限元技术对制动盘内部热应力已经开展了大量的研究工作[12-16]。但是,对于热斑、热裂纹和应力开裂的形成机理目前尚未达成共识,有待进一步研究。研究热斑、热裂纹和热应力的形成机理对于在制动盘服役过程中有效地预防和降低其发生几率具有重要作用。
1 热斑的形成机理
制动盘和闸片实际制动过程中的接触面不是绝对平面,两者之间的接触状态十分复杂。有限元分析的结果表明,制动过程中制动盘摩擦面会发生垂直于摩擦面的法向位移,如图2所示,制动盘和闸片之间的接触是非均匀接触的,最早接触的部位,在压力和摩擦力的作用下,在该局部将会出现局部快速升温,如图3所示。

图2 摩擦面法向位移

图3 温度场分布
摩擦面的局部升温,将造成局部的膨胀增加,在膨胀变形受到摩擦面水平方向的限制时,不可恢复的膨胀变形将发生在摩擦面的法线方向。这种变形加剧了摩擦面凸出区域的进一步凸起变形,导致凸出区域的温度进一步升高,在较高的温度和较大的摩擦剪切力共同作用下,凸出区域内会产生微小的热塑剪切带,热塑剪切带的出现进一步恶化了凸出区域的温度与其他部位温度的不均匀分布,较高的温度和较大的摩擦剪切力的共同作用使凸出区域内热塑剪切带的数量随着制动时间的延长而不断增加。制动盘制动和冷却的周期性重复进行,将导致摩擦面的凸出点区域出现热塑剪切带的聚集,热塑剪切带中伴随着材料的组织变化,图4所示为摩擦面热斑区和非热斑区的组织变化对比图,从图中可以看出,在热斑区出现马氏体组织。
与此同时,这些高温的凸出点区域将在空气中发生高温氧化,颜色变为藏青色,最终在制动盘表面形成所谓的热斑现象,如图1。
从上述热斑的形成机理可知,高速、大制动功率条件下,制动盘摩擦面容易形成热斑。制动盘材料的热容量和导热系数越小,弹性模量和线膨胀系数越大,热斑出现的几率越大。

图4 (a)正常区域组织和(b)热斑区组织
2 疲劳裂纹的形成机理
从宏观角度来看,疲劳裂纹的形成是由于制动盘摩擦面的不均匀温度场分布,导致制动盘摩擦面的不均匀变形,从而在高温区域的内部和边缘形成较大的内应力。当该内应力超过材料在该温度下的强度时,就会出现裂纹萌生,如图5所示。疲劳裂纹的萌生与材料的强度、导热系数、热容量、弹性模量及线膨胀系数等有关。一般来说,材料的热容量和导热系数的大小将决定高温区的温度。萌生的疲劳裂纹在径向和周向拉应力的作用下,沿制动盘的径向扩展。由于高温区材料的晶界强度低,微观上疲劳裂纹将沿着高温区内部及边缘处的材料晶界扩展,形成如图5所示的弯曲不直的热裂纹。

图5 摩擦面热斑区疲劳裂纹
制动盘材料具有较低的热容量和较小的导热系数时,温度会在摩擦面的局部区域聚集而形成较高温度区,由此在该高温区将形成较大的热应力。材料的弹性模量和线膨胀系数越大,温差引起的热应力越大,热裂纹萌生的几率也就越大。此外,如果高温区的温度足以使材料发生组织变化,由于组织变化后体积的变化,高温区处还会由于组织变化而形成应力。因此,高速、大制动功率条件下,制动盘表面很容易形成热裂纹。
3 应力开裂的形成机理
制动盘制动过程中受到多种载荷的共同作用,主要有离心力产生的应力,摩擦制动扭矩产生的应力,不同材料之间由于线膨胀系数的差异导致不同材料的部件之间相互约束而产生的应力,同种材料因结构尺寸差异形成约束而产生的应力。最后两种应力可分别称为材料本征热应力和结构热应力,它们的数值远高于前两者,是制动盘断裂失效的主要作用力[17]。
3.1 制动盘的结构热应力
为分析方便,简化制动盘模型,选取出一个结构单元,如图6(a)所示。在热载荷从制动盘摩擦面的表面施加到制动盘的过程中,由于L1和L2材料之间传热时间上的差异,将导致L1和L2两层之间产生温度差。如果两层之间可以自由变形,L1层的各个方向的变形量可由公式:Δl1=α·(T1-T0)·l计算,L2层的各个方向的变形量可由公式:Δl2=α·(T2-T0)·l计算。实际上,两层材料不能自由变形,它们之间将形成变形约束而产生内应力[18]。这是制动升温产生的膨胀量不同引起的结构热应力,进行以下详细分析。
制动过程中,制动盘在同一时刻出现T1>T2的情况,如果不同层之间发生自由变形,如图6(b)所示,则Δl′>Δl″,将使L1层存在压应力,L2层存在拉应力。但实际情况并非如此,不同层之间存在相互约束,当两层中的内应力低于材料的屈服强度时,在两盘面之间的连接散热筋(圆柱或椭圆柱)的“钉扎”作用下,摩擦面发生的弹性变形见图6(c),此种变形使得图6(a)中A区受压应力,C区受拉应力,这与有限元分析的结果相吻合,如图7所示。当L2层中的拉应力大于相同温度下材料的抗拉强度时,将导致L2中产生断裂失效。在L2层内表面与连接散热筋交接处存在大的拉应力,而且将是裂纹产生的最可能区域。当制动盘中存在最大的T1和T2温度差时,结构热应力将达到最大,发生裂纹的可能性也最大。
当L2层中的内应力高于相同温度下材料的屈服强度时,将导致L1和L2层之间发生图6(d)所示的塑性变形。L1层的伸长量减小,L2的伸长量增加,伸长量达到一个相同值 。但考虑到实际制动条件,此种情况发生的可能性极小。
在不考虑摩擦面变形的情况下,制动盘简化模型的变形如图8(a)、(b)所示。

图6 热载荷引起的径向膨胀变形

图7 径向应力分布云图

图8 散热筋的变形
当热载荷由摩擦面的表面进入制动盘后,由于材料自身的热传导作用将使散热筋的温度升高,散热筋之间的体积差别,使体积不同的散热筋之间存在温度差,从而导致散热筋之间变形不协调,在摩擦面的内表面与连接散热筋交接处产生大应力,摩擦面与体积较大的散热筋的交接处存在拉应力,与体积较小的散热筋的交接处存在压应力。如果两散热筋是自由变形,小体积的散热筋的变形增量为Δh″=α·(Th1-T0)·h,T0为制动的初始温度;Tb1为制动t时刻后小体积散热筋对应的温度。大体积的散热筋的变形增量为Δh′=α·(Th2-T0)·h,Th2为制动t时刻后大体积的散热筋对应的温度,因为Th1>Th2,所以Δh″>Δh′,出于变形的整体协调,两者将发生图8(b)的变形,共同增量为Δh。从而是小体积的散热筋A、B区受压应力,大体积的散热筋C、D区受拉应力,见图8(a),这与有限元分析的结果相吻合,如图9所示。

图9 轴向应力分布云图
下面分析制动过程中制动盘摩擦面沿径向发生的变形,导致周向热应力。为简化分析对摩擦面沿径向作分层假设,如图10(a)所示,当热载荷通过摩擦面的表面施加到制动盘内部,制动盘的温度将升高,如果制动盘的摩擦面均匀升温,不妨设温度升高为ΔT,摩擦面各个半径上的线应变相同均为ε=α·ΔT,其中α为线膨胀系数。变形结果见图10(b),ΔRi=α·ΔT·Ri,i=1,2,3,4。但实际并不是这样,摩擦面内圈的温度受到材料体积分布和装配关系的影响在同一时刻明显低于摩擦面外圈的温度,摩擦面将发生图10(c)所示的变形。
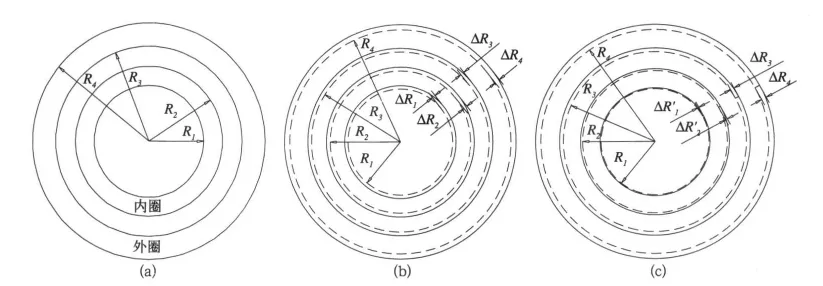
图10 散热面的径向变形
设摩擦面外圈的温升为ΔT,摩擦面内圈的温升ΔT′,且ΔT>ΔT′,摩擦面外圈的线应变为εout=αT·ΔT,摩擦面内圈的线应变为εin=αT′·ΔT′,又αT>αT′(一般情况下材料的热膨胀系数随温度的增加而增加),摩擦面内圈的周向增量为Δc′=(2π·αT′·ΔT′-1)·R1,Δc′表示周向膨胀量,而摩擦面温度均匀时,摩擦面内圈的增量为Δc=(2π·αT·ΔT-1)·R1,Δc表示周向膨胀量,显然,Δc>Δc′,摩擦面内圈受到拉应力,当摩擦面内圈所受的拉应力超过材料的极限强度时,摩擦面将垂直于摩擦面的径向发生断裂失效,尤其是与制动盘爪相连接部位的两侧。这与有限元分析的结果相吻合,如图11所示。

图11 周向应力分布云图
3.2 制动盘的材料本征热应力
压紧装配不同材料的部件,由于材料的线膨胀系数不同,当部件的温度降低时,会导致装配关系的松动,而当部件的温度升高时,将使部件之间进一步压紧,这种压紧力的变化量本质上是由材料的线膨胀系数表征的,因此,称由这种压紧力产生的应力为材料本征热应力。
制动盘、毂、压圈及螺栓之间的装配关系产生了制动盘的轴向机械约束,限制了制动盘和轴的相对位移。当热载荷由摩擦面的表面进入制动盘内部后,由于材料间的热传导作用,毂和压圈的温度也将升高。理想情况下(制动盘、毂、压圈及螺栓的温度和材料均相同时),制动盘的爪及与盘连接部位将发生图12(a)所示的变形,当实际中,由于毂、压圈和螺栓的材料与制动盘的材料不同,当温度升高时,因为螺栓的连接紧固作用,制动盘爪的膨胀被限制,发生图12(b)所示的变形,制动盘、毂和压圈之间的压紧力将增加,从而在爪的根部产生材料本征热应力,其方向沿制动盘的轴向。这与有限元分析的结果相吻合,如图9所示。

图12 热载荷作用时盘爪的变形
3.3 制动盘的径向机械约束热应力
在紧急制动过程中,当热载荷由摩擦面的表面输入制动盘的过程中,制动盘温度升高时,如果制动盘无外部约束而自由膨胀,假设制动盘整体的温度均匀变化,制动盘将发生图13(a)所示的变形,虚线表示变形后的制动盘,但由于制动盘、钢毂及压圈之间紧固连接,严重限制了制动盘爪的径向移动,因此实际发生的变形如图13(b)所示,图13(b)中箭头所指处受到拉应力,方向垂直于摩擦面在应力发生处的径向,此种应力是由于机械约束作用限制了制动盘爪受热膨胀时的径向移动造成的,因此称为机械约束热应力。
通过上述对制动盘的力学分析可知,制动过程中的热载荷是产生应力、变形和裂纹的根源。

图13 机械约束导致的变形
综合考虑结构的约束热应力,材料本征热应力及机械约束热应力的联合作用,制动盘在制动过程中,最可能的裂纹萌生位置位于制动盘爪与摩擦面的搭接部位的两侧,这与有限元分析的结果相吻合,如图14所示。

图14 等效应力分布云图
4 结论
通过研究可以得出以下结论:
(1)热斑是制动盘摩擦面局部高温区的组织变化和高温氧化的结果;
(2)热裂纹是由于制动盘摩擦面高温区的边缘存在较大的内应力而萌生晶界裂纹,在径向和周向拉应力的作用下,裂纹沿晶界径向扩展;
(3)制动盘中不均匀的温度场分布造成不均匀变形,变形受阻形成热应力,在结构约束热应力、材料本征热应力及机械约束热应力的联合作用下,热应力超过材料的高温强度导致制动盘开裂。
[1]J.J.Santini,F.E.Kennedy,experimental investigation of surface temperatures and wear in disk brakes[J].Lubr.Eng.1975,31(8):402-404,413-417.
[2]A.J.Day,T.P.Newcomb,Dissipation of frictional ener gy from the interface of an annular disc brake[J].Proc.Inst.Mech.Eng.D:Transp.Eng.1984,198(11):201-209.
[3]A.A.Evtushenko,E.G.Ivanik,S.Konechny,Determination of the effective heating depth of the disc brake pad[J].Trenie I Iznosv.1998,19(3):318-322.
[4]K.H.Wollenweber,R.Leiter,Function-monitoring brake system:tem-perature monitoring brake system,in:Proceedings of the Institution of Mechanical Engineers[C].International Conference on Braking of Road Vehi-cles,I Mech E,vol.C444/049/93,1993,pp.23-48.
[5]J.Bij we,Nidhi,N.Maju mdar,B.K.Satapathy,Influenc of modified phenolic resins on the fade and recovery behavior of friction materials[J].Wear 259(2005),1 068-1 078.
[6]杨智勇,韩建民,李卫京,陈跃,王金华。铝合金和锻钢制动盘摩擦面热损伤研究[J].铁道学报,2009,4:43-46.
[7]杨智勇.高速客车铝基复合材料制动盘热损伤和结构设计研究[D].北京:北京交通大学,2011.
[8]白以龙,郑哲敏,俞善炳.关于热-塑剪切带的演变[J].力学学报,1986,2:377-383.
[9]A.J.Day and M.Tirovic and T.P.Newconb.Thermal effects and pressure distributions in brakes[J].Proc Instn Mech Engrs.1991,205(2):199-205.
[10]M.Tirovic and A.J.Day.Disc brake interface pressure distributions[J].Proc Instn Mech Engrs.1991,205(2):137-146.
[11]Dae-Jin Ki m,Young-Min Lee et al.Thermal stress analysis for a disk brake of rail way vehicles with consideration of the pressure distribution on a frictional surface[J].Materials Science and Engineering A,2008,483-484(15):456-459.
[12]Chung Kyun Ki m,Boo-Yong Sung etc.Finite element analysis on the thermal behaviors of a disk-pad brake for a high-speed train.Proceedings of the first Asia international conference on tribology[C].Beijing China.1998:95-102.
[13]P.Zagrodzki,K.B.Lam,E.Al Bahkali,J.R.Barber.Nonlinear Transient Behavior of a Sliding System with Frictionally Excited Ther moelastic Instability[J].Jour nal of Tribology,2001,123(10):699-708.
[14]P.Zagtodzki.Analysis of ther momechanical phenomena in multi-disc clutches and brakes[J].Wear,1990,140(2):291-308.
[15]王文静.Si Cp/A356复合材料制动盘温度场应力场数值模拟及热疲劳寿命预测[D].北京:北京交通大学.2003.
[16]吴萌岭.准高速客车制动盘温度场及应力场的计算与分析[J].铁道车辆,1995,33(10):33-38.
[17]PING Xiuer.Thermal stress and fatigue[C].Beijing:National Defence Industry Press,1984:51-82.
[18]LI Weite,HUANG Baohai,BI Zhongbo.Analysis and application of thermal stress theory[C].Beijing:Chinese Electric Power Press,2004:10-50.
